【時間序列】ARIMA模型在鞋服行業銷售預測中的運用
大綱:
-資料處理
-模型構建
-擬合效果
1.資料處理
真實業務資料。來源於特步四川分公司。
資料按照地區可以劃分為:成都/樂山/南充/綿陽等;按品類可以劃分為羽絨服/板鞋/短袖POLO等等。
資料時間跨度:2014年1月~2017年10月
樣本:成都地區跑鞋銷量預測
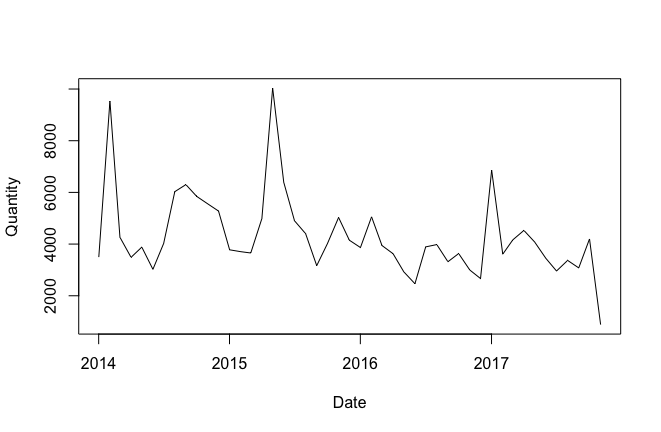
#讀取資料 library(readxl) Shoes2_Chengdu <- read_excel("Desktop/跑鞋區域資料.xlsx", sheet = "成都", col_types = c("date", "numeric")) plot(Shoes2_Chengdu,type="line") attach(Shoes2_Chengdu) Quantity=as.numeric(Quantity) detach(Shoes2_Chengdu)
繪製趨勢圖,對整體趨勢有一個直觀的感受:
節假日因素調整:因為特步在每年的春節,五一,十一等節假日都會舉行促銷活動。除了春節外,其他的節假日都在固定時間。我們所需要調整的是每年春節的不固定日期。
#調整春節因素,2014年春節在一月
a=Shoes2_Chengdu$Quantity[1]
Shoes2_Chengdu$Quantity[1]=Shoes2_Chengdu$Quantity[2]
Shoes2_Chengdu$Quantity[2]=a如果有過小的值,代表是反季商品促銷。(比如羽絨服在夏季的銷量)直接做0值處理,不做預測(因為對銷售決策制定沒有指導意義)。
#剔除過小的值 for (i in 1:47) {if(Shoes2_Chengdu$Quantity[i]<20) Shoes2_Chengdu$Quantity[i]<-0
}
載入時間序列包,將資料整理成時間序列格式。
#載入時間序列程式包
library(tseries)
library(forecast)
library(dplyr)
library(stats)
#轉換成時間序列
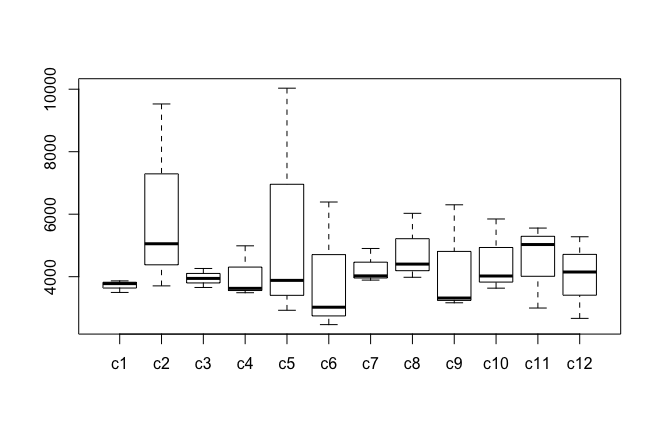
Shoes2_Chengduts<-ts(Shoes2_Chengdu$Quantity[1:47],fre=12,start=c(2014,01))通過箱形圖檢測異常值:箱形圖可以用來觀察資料整體的分佈情況,利用中位數,25/%分位數,75/%分位數,上邊界,下邊界等統計量來來描述資料的整體分佈情況。通過計算這些統計量,生成一個箱體圖,箱體包含了大部分的正常資料,而在箱體上邊界和下邊界之外的,就是異常資料。
#箱型圖檢測異常值
for(i in 1:12){
bp[,i]<-(Shoes2_Chengduts[c(i,i+12,i+24)])}
bptest=boxplot(bp)
bptest$out2.模型構建
選擇ARIMA模型。
首先先檢測模型的平穩性。
#檢測一下平穩性
adf.test(Shoes2_Chengduts) Augmented Dickey-Fuller Test
data: Shoes2_Chengduts
Dickey-Fuller = -7.0728, Lag order = 3, p-value = 0.01
alternative hypothesis: stationary
Warning message:
In adf.test(Shoes2_Chengduts) : p-value smaller than printed p-value可以看出P值很小,我們可以認為模型整體沒有向上或向下的趨勢,基本平穩。
接下來通過ACF圖和PACF圖確定模型階數。
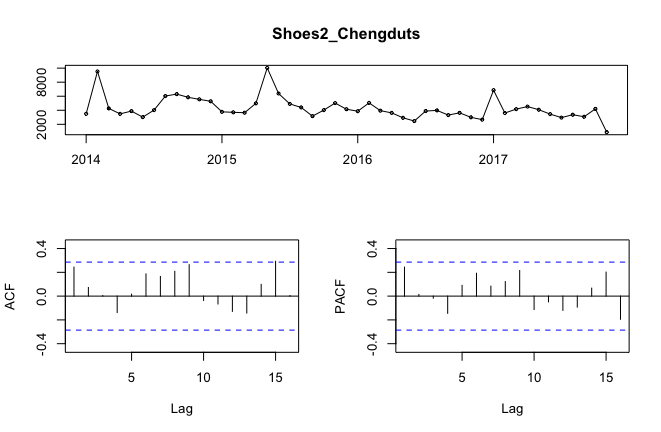
tsdisplay(Shoes2_Chengduts)可以看出ACF圖並沒有明顯的截尾的表現,明視訊記憶體在季節性。實際上我們用常識也可以判斷出來,銷售每年都是有周期性的。所以我們加入季節性因子,考慮12階次差分。
adf.test(diff(Shoes2_Chengduts,12)結論同上,平穩。
Augmented Dickey-Fuller Test
data: diff(Shoes2_Chengduts, 12)
Dickey-Fuller = -4.005, Lag order = 3, p-value = 0.02093
alternative hypothesis: stationary做ACF和PACF圖
tsdisplay(diff(Shoes2_Chengduts,12))
ACF在1階處衰減,PACF在1階處截尾。初步確定Arima階數為(0,0,0)(1,0,1)[12]
arima1<-arima(Shoes2_Chengduts,order=c(0,0,0),seasonal=list(order=c(2,0,1),period=12))我們再來看一下R中自帶的auto命令給出的最優引數。
> auto1<-auto.arima(Shoes2_Chengduts,trace=T)
ARIMA(2,1,2)(1,0,1)[12] with drift : Inf
ARIMA(0,1,0) with drift : 830.1212
ARIMA(1,1,0)(1,0,0)[12] with drift : 826.1885
ARIMA(0,1,1)(0,0,1)[12] with drift : Inf
ARIMA(0,1,0) : 827.9735
ARIMA(1,1,0) with drift : 825.481
ARIMA(1,1,0)(0,0,1)[12] with drift : 826.216
ARIMA(1,1,0)(1,0,1)[12] with drift : Inf
ARIMA(2,1,0) with drift : 824.9653
ARIMA(2,1,1) with drift : Inf
ARIMA(3,1,1) with drift : Inf
ARIMA(2,1,0) : 822.7944
ARIMA(2,1,0)(1,0,0)[12] : 819.5303
ARIMA(2,1,0)(1,0,1)[12] : 820.9409
ARIMA(1,1,0)(1,0,0)[12] : 824.0301
ARIMA(3,1,0)(1,0,0)[12] : 821.3261
ARIMA(2,1,1)(1,0,0)[12] : 820.4318
ARIMA(3,1,1)(1,0,0)[12] : 820.7753
ARIMA(2,1,0)(1,0,0)[12] with drift : 821.4325
Best model: ARIMA(2,1,0)(1,0,0)[12]
要比較模型的擬合效果,通常使用赤池資訊法則(即AIC)來衡量模型的優劣。為了避免過度擬合帶來的偏差,AIC中增加了對多餘變數的懲罰項。我們可以計算AIC的值,越小的AIC的值說明模型的擬合效果最好。
現在我們需要比較兩個模型的AIC值。
arima1$aic
[1] 811.2276> auto1$aic
[1] 819.5303R函式選擇的模型比我們認為比較出來的模型AIC值更高。當然這並不意味著哪個模型“最優”,auto1 的AIC值較高的原因可能是因為加入更多引數,但由於引數值比較大,所以對“過擬合風險”的懲罰項較大。有時候我們需要在衡量過擬合和準確性之間作出抉擇。可以最終兩者都嘗試一下,作出判斷。
3.擬合效果
(1)ARIMA1
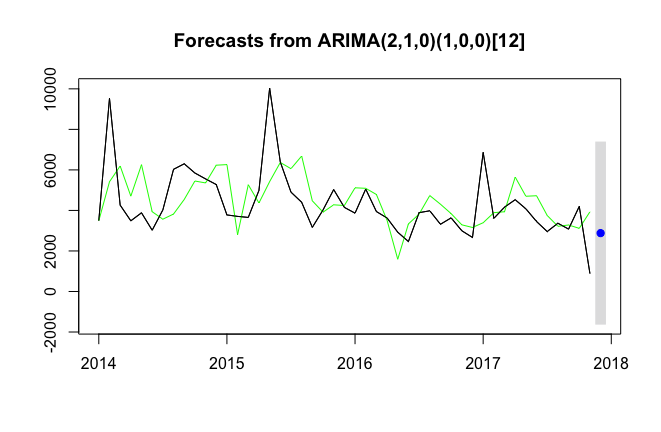
fit1<-forecast(arima1,h=1,level = c(99.5))plot(fit1)
lines(fit1$fitted,col="green")
lines(Shoes2_Chengduts,col='black')
可以看出在16年之前的擬合曲線有滯後現象。明顯感覺有某些因素沒考慮到哦。
再來比較2017年的預測精度。
fitvsture<-data.frame(floor(fit1$fitted[37:47]),Shoes2_Chengdu$Quantity[37:47])
#調整春節因素,2017年春節在1月
a<-fitvsture[1,1]
fitvsture[1,1]=fitvsture[2,1]
fitvsture[2,1]=a#精確度校驗
d<-Shoes2_Chengdu$Quantity[1:10]
for(i in 1:10){
d[i]<-1-(abs(fitvsture[i,1]-fitvsture[i,2])/max(fitvsture[i,1],fitvsture[i,2]))
}
print(fitvsture)
print(d)
error=sum(d[1:10])/10
print(error)> print(fitvsture)
floor.fit1.fitted.37.47.. Shoes2_Chengduts.37.47.
1 3889 6860
2 3393 3609
3 3935 4162
4 5646 4529
5 4699 4080
6 4724 3453
7 3749 2958
8 3216 3368
9 3281 3078
10 3115 4198
11 3933 883
> print(d[1:10])
[1] 0.5669096 0.9401496 0.9454589 0.8021608 0.8682698 0.7309483 0.7890104
[8] 0.9548694 0.9381286 0.7420200
> error=sum(d[1:10])/10
> print(error)
[1] 0.8277926#11月份資料不足,不做預測。不計入精度排名。預測總精度基本上可以達80%。(2)AUTO1
fit1<-forecast(auto1,h=1,level = c(99.5))
plot(fit1)
lines(fit1$fitted,col="green")
lines(Shoes2_Chengduts,col='black')
fitvsture<-data.frame(floor(fit1$fitted[37:47]),Shoes2_Chengduts[37:47])
#調整春節因素,2017年春節在1月
a<-fitvsture[1,1]
fitvsture[1,1]=fitvsture[2,1]
fitvsture[2,1]=a
fitvsture
#精確度校驗
d<-Shoes2_Chengdu$Quantity[1:10]
for(i in 1:10){
d[i]<-1-(abs(fitvsture[i,1]-fitvsture[i,2])/max(fitvsture[i,1],fitvsture[i,2]))
}
print(fitvsture)
print(d[3:10])
error=sum(d[3:10])/7
print(error)> print(fitvsture)
floor.fit1.fitted.37.47.. Shoes2_Chengduts.37.47.
1 3393 6860
2 3889 3609
3 3935 4162
4 5646 4529
5 4699 4080
6 4724 3453
7 3749 2958
8 3216 3368
9 3281 3078
10 3115 4198
11 3933 883
> print(d[1:10])
[1] 0.4946064 0.9280021 0.9454589 0.8021608 0.8682698 0.7309483 0.7890104
[8] 0.9548694 0.9381286 0.7420200
> error=sum(d[1:10])/10
> print(error)
[1] 0.8193475結論:我們可看出,R軟體自動生成的模型AUTO1 的整體擬合效果較ARIMA1較差一些,但兩者相差很小,精確到小數點後兩位後幾乎可以忽略不計。為了降低過擬合風險和提高預測精度,我們最終還是選擇ARIMA1。