51.N皇后(N-Queens)
阿新 • • 發佈:2018-11-13
題目描述
n 皇后問題研究的是如何將 n 個皇后放置在 n×n 的棋盤上,並且使皇后彼此之間不能相互攻擊。
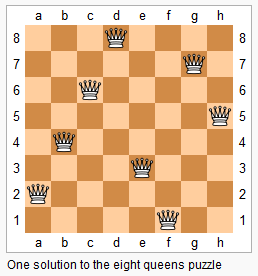
給定一個整數 n,返回所有不同的 n 皇后問題的解決方案。
每一種解法包含一個明確的 n 皇后問題的棋子放置方案,該方案中 ‘Q’ 和 ‘.’ 分別代表了皇后和空位。
示例:
輸入: 4
輸出: [
[".Q…", // 解法 1
“…Q”,
“Q…”,
“…Q.”],
["…Q.", // 解法 2
“Q…”,
“…Q”,
“.Q…”]
]
解釋: 4 皇后問題存在兩個不同的解法。
解題思路
遞迴+迴圈,判斷所有可能位置是否符合要求。
如何判斷?
首先,每行只新增一個Q,可以保證每行不會有重複。然後只要保證該位置對應的列和兩個斜列不會有重複就行了。
建立3個boolean陣列,l[n]代表列,x1[2* n-1]代表左向斜列,x2[2* n-1]代表右向斜列,對於第i行第j列的位置,只要滿足:
l[j]==false && x1[j+i]==false && x2[n-1+i-j]==false
那麼就說明該位置是合乎要求的。
實現程式碼
class Solution {
public List<List<String>> solveNQueens(int n) {
boolean[] l = new boolean[n];
boolean[] x1 = new boolean[2*n-1];
boolean[] x2 = new boolean[2*n-1];
List<List<String>> list = new ArrayList 