前行記錄 - NOIP2018遊記
NOIP2018遊記 - 前行記錄
NOIP2018 完跪……滾回學校考半期 QwQ
這篇不是題解 awa ,題解之後會發布的,畢竟我還沒有AC呢
又及……G2020 陌路笙歌 - 再見(╯▽╰)
感悟
第一次考提高組,之前和將要AFO的G2020一起培訓了很久,感觸頗深~畢竟距離AFO就只剩兩年了,還是抓緊吧
星期五試機的時候有一點爆炸……O(nlogn) 的最長上升子序列都寫掛了。
考試的時候根據策略先掃了一遍所有的題——嗯~好!沒幾道會做的 QwQ
Day1 划水
一群人說AK Day1……然後高中那邊說只有3個人沒AK,然而真的很爆炸
鋪設道路
一開始的奇葩思路:找到最小值,作為分隔點分治;
怎麼找最小點呢?線段樹!-_-|||
然後發現好像很難實現……如果區間裡有多個最小值怎麼辦?
又一想,NOIP day1 t1 線段樹??? Impossible!
再看一眼……貪心!儘可能多填(似乎是很明顯的)!單調棧!(終於對了)
嗯,用了1h做出來
貨幣系統(對,就是這道題寫掛了)
好熟悉的題目……完全揹包!(正解是這樣)
然後莫名遞推式寫掛,多寫了一個 O(n)
賽道修建
出題人非常友好~特殊資料挺多。
先說我自己的做法吧……因為時間不夠,就沒有寫正解,直接騙分:
當m=1時直接跑DFS,加一個最優性剪枝;
當i和i+1相鄰時,就相當於是一個鏈,所以可以二分答案,貪心檢測(即從鏈的端點出發,儘可能選線段,記錄現在的線段總長為tot,當tot>mid即符合條件時,就可以清零tot,找到的路徑條數+1)
其實想到二分+貪心判斷就已經接近正解了,還是有一點可惜。據說正解先二分答案,然後從葉子節點出發儘可能取線段(邊),當達到mid時就形成了一條新的路徑;當兩個路徑會於同一個節點,即LCA,則判斷兩條路徑相連能否>=mid,可以就形成新路徑,否則取較長的路徑連線根節點再往上推。
聽說很水,但是還是掛了;似乎是230的分。
Day2 嘗試
好像有一點Difficult,對於一個初中生真是太不友好了(似乎對於zjx和tly巨佬來說不是這樣的……)
旅行
比較簡單的貪心;
從1出發;
對於樹形結構先走較小點;
然後又一個環的情況掛了……時間複雜度沒分析對,本來 O(n^2)能過,但是就沒寫,以為會 TLE;
填數遊戲
看題目的時候第一眼——結論題!!!
然後第一題放棄後就開始死推結論,然後推出來一個似乎是正確的結論——
如果A,B兩個位置,A在B的右上方,則A的填的數字不能大於B;
驗證了一下2*2的情況,是對的(開心);然後手算3*3……為什麼我算出來是144?!
心態就崩了……最後只好將6*6的所有答案通過DFS打表跑出來(效果不錯)
然後賽後發現很多同學和我的結論一樣……都卡住了,於是我們開始討論——我把我有點疑惑的一點畫出了圖:
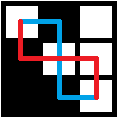
上面黑色塊填的數字是1,看得出來藍色路徑為 "RDDDR",紅色路徑為"DRRRD",但是藍色路徑經過的點為"01010",紅色路徑經過的點為"01000"……
尷尬……結論完全錯誤
保衛王國
第一眼樹形DP(開心)
然後發現多組詢問,沉思QwQ
想不出來,就只好寫 O(n,m) 的,也就是對於每一次詢問都做一次 O(n) 的DP
but……樹形DP寫掛了啊——因為如果當前點是詢問中要求必須選/不選的點,dp狀態中的一個值就需要賦值為INF,但是我把這一步操作放在了訪問當前節點的兒子時處理的……也就是說如果當前節點是被限制的一個節點,在訪問它的一個合法兒子(不是父親)時,我就把某一個dp狀態設為INF(比如當點u不能選時,表示“選擇u點”的狀態就是INF)。但是會出現一個問題——限制葉子節點時,因為葉子節點沒有子節點,所以它的不合法狀態就不會標記為INF,就掛了。
關鍵是隻要存在一個這樣的詢問,整個資料就會掛掉QwQ
嘆息
唉,以前常喜歡說 “路還很長,要慢慢走” ,但現在看來路雖長,但時間卻不多了啊!
已經初三了,下一年就是高一,再過兩年,沒進省隊就要AFO了(雖然不是真正的OIer,但是還是不願提到AFO這個終會到來的事實)
後面的路得加緊走了(我設立了一個計劃,刷《挑戰程式設計競賽》的習題,儘可能每週6道)
希望大家能共同進步(膜誰也沒用,考場上還是孤單一人)
