首先，這個演算法可以如下表述：

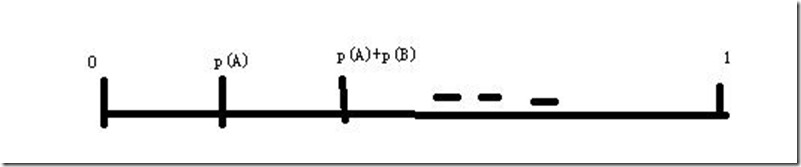
如果已知A類物件生成概率為P(A)，B類物件生成概率為P(B),C類物件···，K類物件，他們的概率總和為1，問如何在A~K中隨機生成一個物件

演算法理解如下：

即我們需要先對0~1區段按照概率大小劃分長度，設隨機生成一個0~1之間的數，這種隨機數生成結果是在0~1均勻分佈的，然後看其究竟落在哪個概率區段即為生成哪種物件

演算法程式碼：

package test;

import org.junit.Test;

public class Roulette {

    @Test
    public  void test() {
        double[] P={0.2,0.3,0.5};//假設的概率分佈
        int appearnum=0;
        for(int i=0;i<100;i++){
            int result=roulette(P);
            if(result==2)//統計第2類物件生成的數目，可以看出大致為50%的生成概率
                appearnum++;
        }
        System.out.println(appearnum);
    }
    /**
     * 輪盤賭函式
     * @param P 各類物件概率分佈
     * @return 生成的物件類
     */
    private int roulette(double[] P){
        
        double rand=Math.random();
        double pointer=0;//pointer指示每個區段的右邊界，從左往右掃描判斷
        for(int i=0;i<P.length;i++){
            pointer+=P[i];
            if(rand<=pointer)
                return i;
        }
        return -1;
    }

}

首先，這個演算法可以如下表述：

如果已知A類物件生成概率為P(A)，B類物件生成概率為P(B),C類物件···，K類物件，他們的概率總和為1，問如何在A~K中隨機生成一個物件

演算法理解如下：

即我們需要先對0~1區段按照概率大小劃分長度，設隨機生成一個0~1之間的數，這種隨機數生成結果是在0~1均勻分佈的，然後看其究竟落在哪個概率區段即為生成哪種物件

演算法程式碼：

package test;

import org.junit.Test;

public class Roulette {

    @Test
    public  void test() {
        double[] P={0.2,0.3,0.5};//假設的概率分佈
        int appearnum=0;
        for(int i=0;i<100;i++){
            int result=roulette(P);
            if(result==2)//統計第2類物件生成的數目，可以看出大致為50%的生成概率
                appearnum++;
        }
        System.out.println(appearnum);
    }
    /**
     * 輪盤賭函式
     * @param P 各類物件概率分佈
     * @return 生成的物件類
     */
    private int roulette(double[] P){
        
        double rand=Math.random();
        double pointer=0;//pointer指示每個區段的右邊界，從左往右掃描判斷
        for(int i=0;i<P.length;i++){
            pointer+=P[i];
            if(rand<=pointer)
                return i;
        }
        return -1;
    }

}