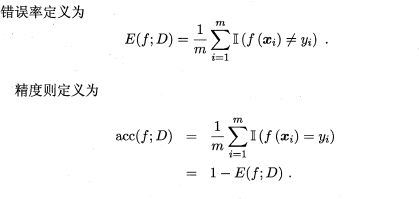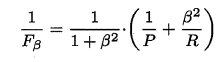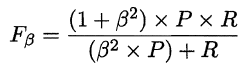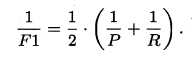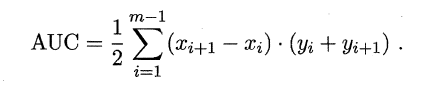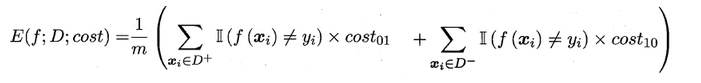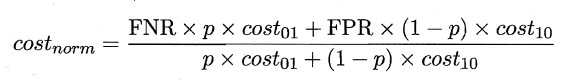2.5 效能度量

效能度量（performance measure）是衡量模型泛化能力的評價標準，在對比不同模型的能力時，使用不同的效能度量往往會導致不同的評判結果。本節除2.5.1外，其它主要介紹分類模型的效能度量。

2.5.1 最常見的效能度量

在迴歸任務中，即預測連續值的問題，最常用的效能度量是“均方誤差”（mean squared error）,很多的經典演算法都是採用了MSE作為評價函式，想必大家都十分熟悉。

在分類任務中，即預測離散值的問題，最常用的是錯誤率和精度，錯誤率是分類錯誤的樣本數佔樣本總數的比例，精度則是分類正確的樣本數佔樣本總數的比例，易知：錯誤率+精度=1。

2.5.2 查準率/查全率/F1

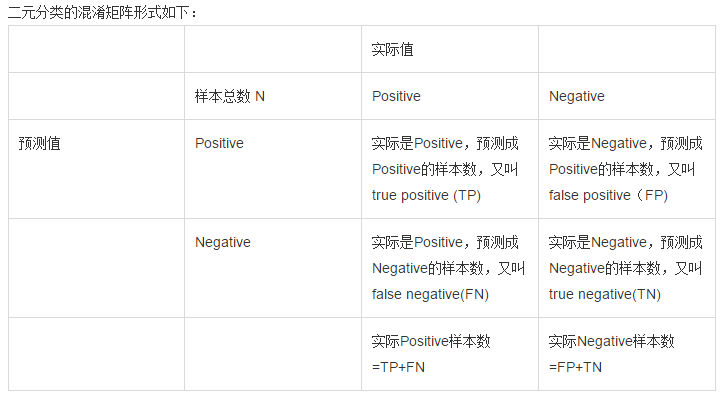
錯誤率和精度雖然常用，但不能滿足所有的需求，例如：在推薦系統中，我們只關心推送給使用者的內容使用者是否感興趣（即查準率），或者說所有使用者感興趣的內容我們推送出來了多少（即查全率）。因此，使用查準/查全率更適合描述這類問題。對於二分類問題，分類結果混淆矩陣與查準/查全率定義如下：

初次接觸時，FN與FP很難正確的理解，按照慣性思維容易把FN理解成：False->Negtive，即將錯的預測為錯的，這樣FN和TN就反了，後來找到一張圖，描述得很詳細，為方便理解，把這張圖也貼在了下邊：

正如天下沒有免費的午餐，查準率和查全率是一對矛盾的度量。例如我們想讓推送的內容儘可能使用者全都感興趣，那隻能推送我們把握高的內容，這樣就漏掉了一些使用者感興趣的內容，查全率就低了；如果想讓使用者感興趣的內容都被推送，那只有將所有內容都推送上，寧可錯殺一千，不可放過一個，這樣查準率就很低了。

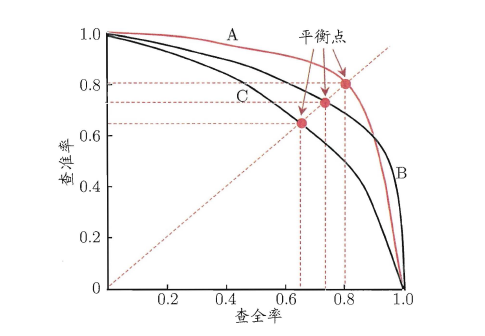
“P-R曲線”正是描述查準/查全率變化的曲線，P-R曲線定義如下：根據學習器的預測結果（一般為一個實值或概率）對測試樣本進行排序，將最可能是“正例”的樣本排在前面，最不可能是“正例”的排在後面，按此順序逐個把樣本作為“正例”進行預測，每次計算出當前的P值和R值，如下圖所示：

P-R曲線如何評估呢？若一個學習器A的P-R曲線被另一個學習器B的P-R曲線完全包住，則稱：B的效能優於A。若A和B的曲線發生了交叉，則誰的曲線下的面積大，誰的效能更優。但一般來說，曲線下的面積是很難進行估算的，所以衍生出了“平衡點”（Break-Event Point，簡稱BEP），即當P=R時的取值，平衡點的取值越高，效能更優。

P和R指標有時會出現矛盾的情況，這樣就需要綜合考慮他們，最常見的方法就是F-Measure，又稱F-Score。F-Measure是P和R的加權調和平均，即：

特別地，當β=1時，也就是常見的F1度量，是P和R的調和平均，當F1較高時，模型的效能越好。

有時候我們會有多個二分類混淆矩陣，例如：多次訓練或者在多個數據集上訓練，那麼估算全域性效能的方法有兩種，分為巨集觀和微觀。簡單理解，巨集觀就是先算出每個混淆矩陣的P值和R值，然後取得平均P值macro-P和平均R值macro-R，在算出Fβ或F1，而微觀則是計算出混淆矩陣的平均TP、FP、TN、FN，接著進行計算P、R，進而求出Fβ或F1。

2.5.3 ROC與AUC

如上所述：學習器對測試樣本的評估結果一般為一個實值或概率，設定一個閾值，大於閾值為正例，小於閾值為負例，因此這個實值的好壞直接決定了學習器的泛化效能，若將這些實值排序，則排序的好壞決定了學習器的效能高低。ROC曲線正是從這個角度出發來研究學習器的泛化效能，ROC曲線與P-R曲線十分類似，都是按照排序的順序逐一按照正例預測，不同的是ROC曲線以“真正例率”（True Positive Rate，簡稱TPR）為橫軸，縱軸為“假正例率”（False Positive Rate，簡稱FPR），ROC偏重研究基於測試樣本評估值的排序好壞。

簡單分析影象，可以得知：當FN=0時，TN也必須0，反之也成立，我們可以畫一個佇列，試著使用不同的截斷點（即閾值）去分割佇列，來分析曲線的形狀，（0,0）表示將所有的樣本預測為負例，（1,1）則表示將所有的樣本預測為正例，（0,1）表示正例全部出現在負例之前的理想情況，（1,0）則表示負例全部出現在正例之前的最差情況。限於篇幅，這裡不再論述。

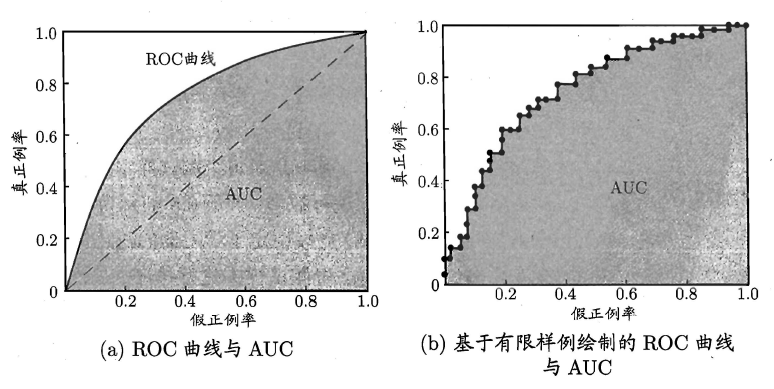
現實中的任務通常都是有限個測試樣本，因此只能繪製出近似ROC曲線。繪製方法：首先根據測試樣本的評估值對測試樣本排序，接著按照以下規則進行繪製。

同樣地，進行模型的效能比較時，若一個學習器A的ROC曲線被另一個學習器B的ROC曲線完全包住，則稱B的效能優於A。若A和B的曲線發生了交叉，則誰的曲線下的面積大，誰的效能更優。ROC曲線下的面積定義為AUC（Area Uder ROC Curve），不同於P-R的是，這裡的AUC是可估算的，即AOC曲線下每一個小矩形的面積之和。易知：AUC越大，證明排序的質量越好，AUC為1時，證明所有正例排在了負例的前面，AUC為0時，所有的負例排在了正例的前面。

2.5.4 代價敏感錯誤率與代價曲線

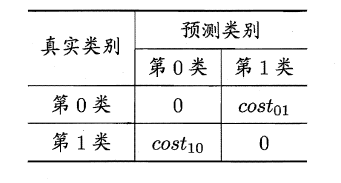
上面的方法中，將學習器的犯錯同等對待，但在現實生活中，將正例預測成假例與將假例預測成正例的代價常常是不一樣的，例如：將無疾病–>有疾病只是增多了檢查，但有疾病–>無疾病卻是增加了生命危險。以二分類為例，由此引入了“代價矩陣”（cost matrix）。

在非均等錯誤代價下，我們希望的是最小化“總體代價”，這樣“代價敏感”的錯誤率（2.5.1節介紹）為：

同樣對於ROC曲線，在非均等錯誤代價下，演變成了“代價曲線”，代價曲線橫軸是取值在[0,1]之間的正例概率代價，式中p表示正例的概率，縱軸是取值為[0,1]的歸一化代價。

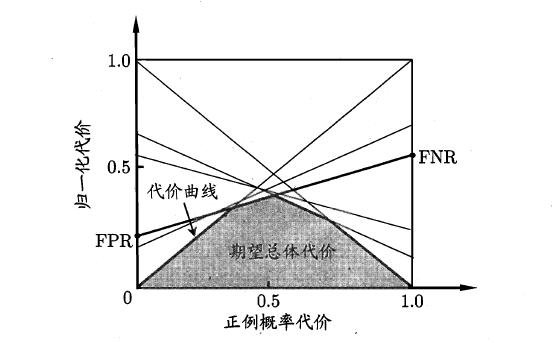
代價曲線的繪製很簡單：設ROC曲線上一點的座標為(TPR，FPR) ，則可相應計算出FNR，然後在代價平面上繪製一條從(0，FPR) 到(1，FNR) 的線段，線段下的面積即表示了該條件下的期望總體代價；如此將ROC 曲線土的每個點轉化為代價平面上的一條線段，然後取所有線段的下界，圍成的面積即為在所有條件下學習器的期望總體代價，如圖所示：

在此模型的效能度量方法就介紹完了，以前一直以為均方誤差和精準度就可以了，現在才發現天空如此廣闊~