1. 理論基礎知識

LDA用來提取線性特徵，這種特徵的目標在於最大化between-class separation以及最小化within-class sepration。LDA可以給訓練資料擬合一個高斯混合模型：用x表示observable sample,用y表示the latent variable，則類條件概率可以表示為

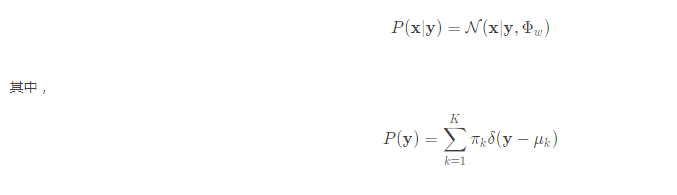
這種混合模型只能表示有限的K類，如果想拓展這個概率模型，嚷他能夠模型中出現在訓練資料中的其他類。為此，把y的先驗設為連續的，為方便運算，讓y的先驗服從高斯分佈（高斯 PLDA，G-PLDA）：

Kaldi訓練PLDA的程式碼閱讀
Kaldi中PLDA實現的相關程式碼主要在src/ivectorbin/下的四個檔案中：plda.h， plda.cc, ivector-compute-plda.cc, ivector-plda-scoring.cc。
為了方便閱讀，接下來我會把主幹部分貼出來。
我們首先來看ivector-compute-plda.cc, 從這裡我們可以知道實現中用到了哪些類。
 

PldaEstimationConfig plda_config; //這裡指定了E-M的迭代次數，預設是10次
SequentialTokenVectorReader spk2utt_reader(spk2utt_rspecifier);
RandomAccessBaseFloatVectorReader ivector_reader(ivector_rspecifier);
PldaStats plda_stats;  //生成一個plda_stats例項，主要用來存放資料
for (; !spk2utt_reader.Done(); spk2utt_reader.Next()) {
  std::string spk = spk2utt_reader.Key();
  const std::vector<std::string> &uttlist = spk2utt_reader.Value();
  if (uttlist.empty()) {
    KALDI_ERR << "Speaker with no utterances.";
  }
  std::vector<Vector<BaseFloat> > ivectors;
  ivectors.reserve(uttlist.size());

  for (size_t i = 0; i < uttlist.size(); i++) {
    std::string utt = uttlist[i];
    if (!ivector_reader.HasKey(utt)) {
      KALDI_WARN << "No iVector present in input for utterance " << utt;
      num_utt_err++;
    } else {
      ivectors.resize(ivectors.size() + 1);
      ivectors.back() = ivector_reader.Value(utt);
      num_utt_done++;
    }
  }

  if (ivectors.size() == 0) {
    KALDI_WARN << "Not producing output for speaker " << spk
               << " since no utterances had iVectors";
    num_spk_err++;
  } else {
    Matrix<double> ivector_mat(ivectors.size(), ivectors[0].Dim());
    for (size_t i = 0; i < ivectors.size(); i++)
      ivector_mat.Row(i).CopyFromVec(ivectors[i]);
    double weight = 1.0; // The code supports weighting but
                         // we don't support this at the command-line
                         // level yet.
    plda_stats.AddSamples(weight, ivector_mat);
    num_spk_done++;
  }
}
plda_stats.Sort();  // Sort class_info_ to make num_examples in increasing order. 
PldaEstimator plda_estimator(plda_stats);
Plda plda;
plda_estimator.Estimate(plda_config, &plda);
WriteKaldiObject(plda, plda_wxfilename, binary);
--------------------- 
作者：ShaunSXLiu 
來源：CSDN 
原文：https://blog.csdn.net/Liusongxiang666/article/details/83024845 
版權宣告：本文為博主原創文章，轉載請附上博文連結！
 

從這段程式碼中，我們看到主要用到了三個類：PldaStats, PldaEstimator 和 Plda。接下來我們一個一個來看。
PldaStats 主要用來存放i-vecrtor資料以及一些統計引數。它的主要資料有：

// 假設weight都是預設引數1.0
int32 dim_;                    // i-vector的維度
int64 num_classes_;     // 說話人的個數
int64 num_examples_; // 所有說話人的總i-vector個數 N
double class_weight_; // 類的個數，即說話人的個數 K
double example_weight_; // 所有說話人的總i-vector個數 N
Vector<double> sum_;     // K個說話人平均i-vector之和
SpMatrix<double> offset_scatter_; //就是第一部分所說的S矩陣
--------------------- 
作者：ShaunSXLiu 
來源：CSDN 
原文：https://blog.csdn.net/Liusongxiang666/article/details/83024845 
版權宣告：本文為博主原創文章，轉載請附上博文連結！
 

PldaStats還有一個比較重要的結構成員 ClassInfo, std::vector<ClassInfo> class_info_中每個元素是(weight, mean, num_examples)。PldaStats的成員函式AddSamples主要用來新增資料。程式碼如下, 註釋就加在程式碼中了：
 

void PldaStats::AddSamples(double weight,
                           const Matrix<double> &group) {
  if (dim_ == 0) {
    Init(group.NumCols());  // initialize all the PldaStats parameters. See line 327.
  } else {
    KALDI_ASSERT(dim_ == group.NumCols());
  }
  int32 n = group.NumRows(); // number of examples for this class
  Vector<double> *mean = new Vector<double>(dim_);
  mean->AddRowSumMat(1.0 / n, group);   // Does *this = 1.0/n * (sum of rows of M) + 1.0 * *this

  // The following two lines computes MM^T - n * mean mean^T, i.e., the scatter matrix within one speaker.
  offset_scatter_.AddMat2(weight, group, kTrans, 1.0); //(*this) = 1.0*(*this) + weight * M^T * M
  // the following statement has the same effect as if we
  // had first subtracted the mean from each element of
  // the group before the statement above.
  offset_scatter_.AddVec2(-n * weight, *mean);  // rank-one update, this <– this + alpha v v'


  class_info_.push_back(ClassInfo(weight, mean, n));

  num_classes_ ++; 
  num_examples_ += n;               // \sum_{k=1}^K n_k
  class_weight_ += weight;          // K
  example_weight_ += weight * n;    // \sum_{k=1}^K n_k

  sum_.AddVec(weight, *mean);  // add mean_k to sum_
--------------------- 
作者：ShaunSXLiu 
來源：CSDN 
原文：https://blog.csdn.net/Liusongxiang666/article/details/83024845 
版權宣告：本文為博主原創文章，轉載請附上博文連結！

值得注意的是：group 是一個存放一個說話人所有i-vector的矩陣，其中的每一行代表一個i-vector。mean 求的是 。用M 來表示i-vector矩陣，在每次呼叫AddSamples函式時，offset_scatter就加上 , 即一個說話人的scatter matrix。

PldaEstimator是一個非常重要的類，PLDA的訓練主要是通過它來實現。我們下來看一下它含有那些主要的資料成員。

void PldaEstimator::GetStatsFromIntraClass() {
  within_var_stats_.AddSp(1.0, stats_.offset_scatter_);  // equivalent to copying stats_.offset_scatter_ to within_var_stats_: The value computed is (1.0 * within_var_stats_[i][j]) + offset_scatter_[i][j].
  // Note: in the normal case, the expression below will be equal to the sum
  // over the classes, of (1-n), where n is the #examples for that class.  That
  // is the rank of the scatter matrix that "offset_scatter_" has for that
  // class. [if weights other than 1.0 are used, it will be different.]
  within_var_count_ += (stats_.example_weight_ - stats_.class_weight_);  // N - K, to get the unbiased covariance estimator?
}
--------------------- 
作者：ShaunSXLiu 
來源：CSDN 
原文：https://blog.csdn.net/Liusongxiang666/article/details/83024845 
版權宣告：本文為博主原創文章，轉載請附上博文連結！

第三步是訓練PLDA的主要步驟：基本上對應上面E-M中列出的公式。

void PldaEstimator::GetStatsFromClassMeans() {
  SpMatrix<double> between_var_inv(between_var_);  // define \Phi_b^{-1} initialized with last-step \Phi_b
  between_var_inv.Invert();                        // now is \Phi_b^{-1}
  SpMatrix<double> within_var_inv(within_var_);    // the same as steps above
  within_var_inv.Invert();
  // mixed_var will equal (between_var^{-1} + n within_var^{-1})^{-1}.
  SpMatrix<double> mixed_var(Dim());               // define \hat \Phi
  int32 n = -1; // the current number of examples for the class.

  for (size_t i = 0; i < stats_.class_info_.size(); i++) {
    const ClassInfo &info = stats_.class_info_[i];
    double weight = info.weight;
    if (info.num_examples != n) {
      n = info.num_examples;
      mixed_var.CopyFromSp(between_var_inv);
      mixed_var.AddSp(n, within_var_inv);
      mixed_var.Invert();
    }
    Vector<double> m = *(info.mean); // the mean for this class.
    m.AddVec(-1.0 / stats_.class_weight_, stats_.sum_); // remove global mean
    Vector<double> temp(Dim()); // n within_var^{-1} m
    temp.AddSpVec(n, within_var_inv, m, 0.0); //Add symmetric positive definite matrix times vector: this <– n*within_var_inv*m.
    Vector<double> w(Dim()); // w, as defined in the comment.
    w.AddSpVec(1.0, mixed_var, temp, 0.0);  // w = (between_var^{-1} + n within_var^{-1})^{-1} * n within_var^{-1} m
    Vector<double> m_w(m); // m - w
    m_w.AddVec(-1.0, w);
    between_var_stats_.AddSp(weight, mixed_var);
    between_var_stats_.AddVec2(weight, w);    // \Phi_b = (between_var^{-1} + n within_var^{-1})^{-1} + w w^T
    between_var_count_ += weight;             // to count num of classes
    within_var_stats_.AddSp(weight * n, mixed_var);
    within_var_stats_.AddVec2(weight * n, m_w);   // \Phi_w = n * ((between_var^{-1} + n within_var^{-1})^{-1} + (m-w)(m-w)^T)
    within_var_count_ += weight;
  }
}
--------------------- 
作者：ShaunSXLiu 
來源：CSDN 
原文：https://blog.csdn.net/Liusongxiang666/article/details/83024845 
版權宣告：本文為博主原創文章，轉載請附上博文連結！

void PldaEstimator::GetOutput(Plda *plda){
 plda->mean_=stats_.sum_;
 plda-mean_.Scale(1.0/stats_.class_weight_);
 KALDI_LOG<<"Norm of mean of ivvector distribution is"<<plda->mean_.Norm(2.0);

Matrix<double> transform1(Dim(),Dim());
ComputeNormslizingTransform(with_var_,&transform1);
//now transform is a matrix that if we project with it,within_var_ becomes unit.

  // between_var_proj is between_var after projecting with transform1.
SpMatrix<double>between_var_proj(Dim());
between_var_proj.AddMat25p(1.0,transform1,KnoTrans,Between_var,0.0); // alpha * M * A * M^T.

Matrix<double>U(Dim(),Dim());
Vector<double>s(Dim());
// Do symmetric eigenvalue decomposition between_var_proj = U diag(s) U^T,
  // where U is orthogonal.
betwen_var_proj.Eig(&s,&u);

KALDI_ASSERT(s.Min()>=0.0);
int32 n;
s.ApplyFloor(0.0,&n);
if(n>0){
  KALDI_WARN<<"Floored"<<n<<"eignvalues of between-class"<<"variance to zero.";
        }

// Sort from greatest to smallest eigenvalue  //從最大特徵值到最小特徵值排序

SortSvd(&s,&U);
/ The transform U^T will make between_var_proj diagonal with value s
  // (i.e. U^T U diag(s) U U^T = diag(s)).  The final transform that
  // makes within_var_ unit and between_var_ diagonal is U^T transform1,
  // i.e. first transform1 and then U^T.
  //變換U ^ T將使得from_var_proj對角線具有值s（即，U ^ T U diag（s）U U ^ T = diag（s））。 //使within_var_ unit和between_var_對角線的最終變換是U ^ T transform1，即。 首先是transform1然後是U ^ T.
plda->transform_.Resize(Dim(), Dim());
  plda->transform_.AddMatMat(1.0, U, kTrans, transform1, kNoTrans, 0.0);  // U^T transform1
  plda->psi_ = s;

  KALDI_LOG << "Diagonal of between-class variance in normalized space is " << s;

  if (GetVerboseLevel() >= 2) { // at higher verbose levels, do a self-test
                                // (just tests that this function does what it
                                // should).
    SpMatrix<double> tmp_within(Dim());
    tmp_within.AddMat2Sp(1.0, plda->transform_, kNoTrans, within_var_, 0.0);
    KALDI_ASSERT(tmp_within.IsUnit(0.0001));
    SpMatrix<double> tmp_between(Dim());
    tmp_between.AddMat2Sp(1.0, plda->transform_, kNoTrans, between_var_, 0.0);
    KALDI_ASSERT(tmp_between.IsDiagonal(0.0001));
    Vector<double> psi(Dim());
    psi.CopyDiagFromSp(tmp_between);
    AssertEqual(psi, plda->psi_);
  }
  plda->ComputeDerivedVars();  // off_set_ = -1.0 * (U^T V)^{-1} m
}

PLDA打分
Kaldi中的PLDA參考是Sergey Ioffe的這篇paper的打分方法。我們能夠把一個類的多個sample整合進一個模型，從而提高效能。