typedef long long LL;

const LL mod=1e9+7;
const int maxn=3e5+10;
const int N=3e5;

int jie[maxn],ni[maxn];
void init()
{
    jie[0]=jie[1]=1;

    for(int i=2;i<=N;i++)
        jie[i]=1LL*jie[i-1]*i%mod; ///前i項的階乘

    ni[N]=pow(jie[N],mod-2); ///逆元，呼叫pow函式時應 用LL

    for(int i=N;i>=1;i--) ///線性篩逆元
    {
        ni[i-1]=1LL*ni[i]*i%mod;
    }
}
 

ni[N]=(1*2*3*...*N)^(mod-2)=(1*2*3*...*(N-1))^(mod-2)*N^(mod-2)

ni[N-1]=(1*2*3*...*(N-1))^(mod-2)=ni[N]/(N^(mod-2),

我們由費馬小定理可知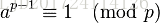，  （a不是p的倍數，也就是p不能整除a，那麼p是質數，就一定滿足）。

 , 變形得 a*a^(p-2)≡1(mod p)，答案已經很明顯了:若a,p互質,a^(p-2)的逆元就是a，即N^(mod-2)的逆元就是N，

故ni[N-1]=ni[N]*N。