邊緣檢測是影象處理和計算機視覺中的基本問題，邊緣檢測的目的是標識數字影象中變化明顯的點。影象屬性中的顯著變化通常反映了屬性的重要事件和變化，這些包括深度上的不連續、表面方向不連續、物質屬性變化和場景照明變化， 邊緣檢測大幅度地減少了資料量，並且剔除了可以認為不相關的資訊，保留了影象重要的結構屬性。常用的描邊也是先進行邊緣然後再進行邊緣處理。

一、卷積

  卷積（Convolution）本質上來講就是一種數學運算，跟減加乘除沒有區別。在影象處理中用一個模板（這個模板就是卷積核（kernel））和一幅影象進行卷積，對於影象上的一個點，讓模板的原點和該點重合，然後模板上的點和影象上對應的點相乘，最後將各點的積相加，就得到該點的卷積值。然後移動模板對正下一個點，對影象上的每個點都這樣處理。卷積是一種積分運算，可以看作加權求和，可以用來消除噪聲、特徵增強， 把一個點的畫素值用它周圍的點的畫素值的加權平均代替。
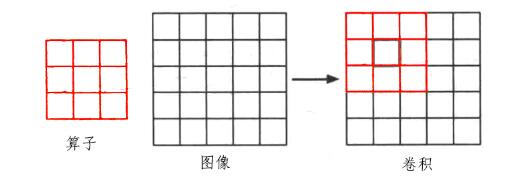
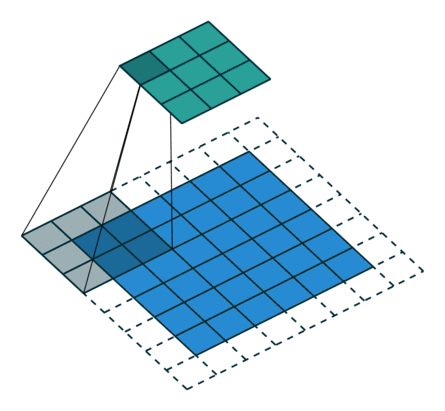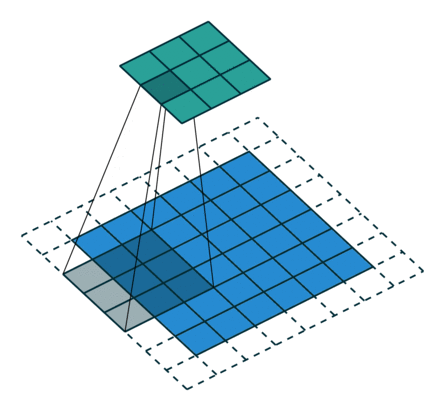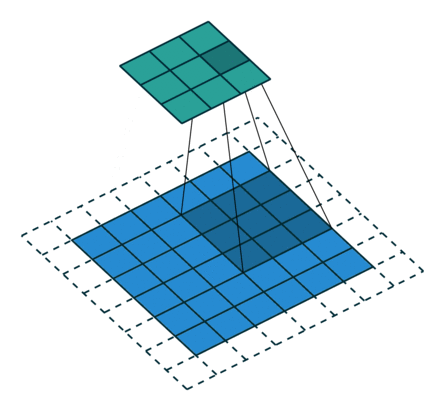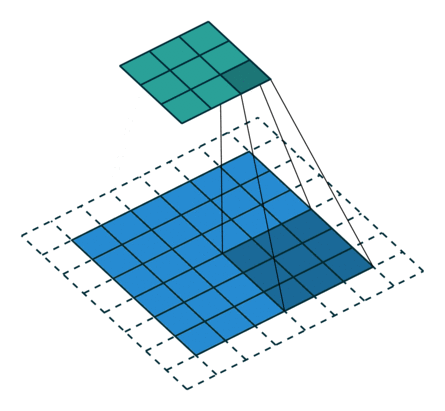
  卷積核通常是一個四方形風格結構（如2x2、3x3），該網格區域內的每一個方格都有一個權重值。當對影象中的某個畫素進行卷積時，我們會把卷積核的中心放置於該畫素上，如下圖所示，翻轉核之後再依次計算核中每個元素和其覆蓋的影象畫素值的乘積，最後將各乘積累加，得到的結果就是該畫素的新畫素值。然後移動卷積核到下一個畫素，進行同樣的處理，至到所有畫素都處理完。

  卷積聽起來很難，在圖形處理中其實就這麼簡單，但卷積可以實現很多常見的影象處理效果，例如影象模糊、邊緣檢測等等。

二、sobel運算元

  卷積的神奇之處在於選擇的卷積核，用於邊緣檢測的卷積核也叫邊緣檢測運算元，先後有好幾種邊緣檢測運算元被提出來。

• Roberts運算元

  Roberts運算元採用對角線方向相鄰兩畫素之差近似梯度幅值檢測邊緣。檢測水平和垂直邊緣的效果好於斜向邊緣，定位精度高，但對噪聲敏感。

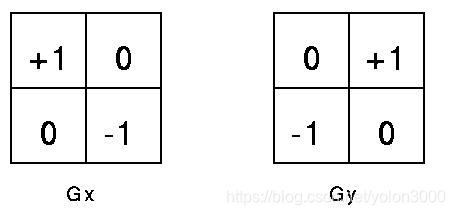
• Prewitt運算元

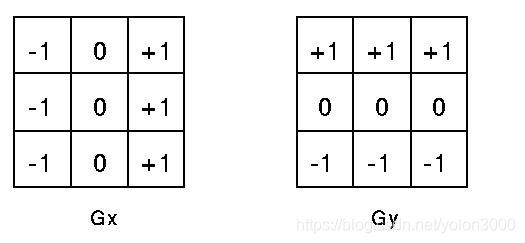
  Prewitt運算元利用畫素點上下、左右鄰點灰度差，在邊緣處達到極值檢測邊緣。對噪聲具有平滑作用，但是定位精度不夠高。

• Sobel運算元

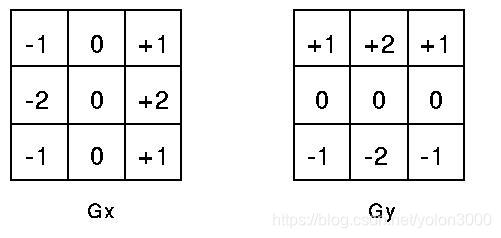
  Sobel 運算元主要用作邊緣檢測，它是一個離散的一階差分運算元，用來計算影象亮度函式的一階梯度之近似值。在影象的任何一點使用此運算元，將會產生該點對應的梯度向量或是其法向量。與Prewitt運算元相比，Sobel運算元對於畫素的位置的影響做了加權，可以降低邊緣模糊程度，因此效果更好。

  該運算元包含兩組3x3的矩陣，分別為橫向及縱向，將之與影象作平面卷積，即可分別得出橫向及縱向的亮度差分近似值。如果以A代表原始影象，Gx及Gy分別代表經橫向及縱向邊緣檢測的影象灰度值，其公式如下：

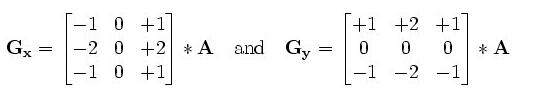
  具體計算如下：

Gx = (-1)*f(x-1, y-1) + 0*f(x,y-1) + 1*f(x+1,y-1)

      +(-2)*f(x-1,y) + 0*f(x,y)+2*f(x+1,y)

      +(-1)*f(x-1,y+1) + 0*f(x,y+1) + 1*f(x+1,y+1)

     = [f(x+1,y-1)+2*f(x+1,y)+f(x+1,y+1)]-[f(x-1,y-1)+2*f(x-1,y)+f(x-1,y+1)]

 

Gy =1* f(x-1, y-1) + 2*f(x,y-1)+ 1*f(x+1,y-1)

      +0*f(x-1,y) 0*f(x,y) + 0*f(x+1,y)

      +(-1)*f(x-1,y+1) + (-2)*f(x,y+1) + (-1)*f(x+1, y+1)

     = [f(x-1,y-1) + 2f(x,y-1) + f(x+1,y-1)]-[f(x-1, y+1) + 2*f(x,y+1)+f(x+1,y+1)]

  其中f(a,b), 表示影象(a,b)點的灰度值；
  影象的每一個畫素的橫向及縱向灰度值通過以下公式結合，來計算該點灰度的大小：

   $G=\sqrt{Gx^2+Gy^2}$

  通常，為了提高效率 使用不開平方的近似值：

   $G=|Gx|+|Gy|$

  如果梯度G大於某一閥值則認為該點(x,y)為邊緣點。Sobel運算元根據畫素點上下、左右鄰點灰度加權差，在邊緣處達到極值這一現象檢測邊緣。對噪聲具有平滑作用，提供較為精確的邊緣方向資訊，邊緣定位精度不夠高。當對精度要求不是很高時，是一種較為常用的邊緣檢測方法。

  Sobel運算元的計算速度比Roberts運算元慢，但其較大的卷積核在很大程度上平滑了輸入影象，使運算元對噪聲的敏感性降低。與Roberts運算元相比，通常也會為相似的邊緣產生更高的輸出值。與Roberts運算元一樣，操作時輸出值很容易溢位僅支援小整數畫素值(例如8位整數影象)的影象型別的最大允許畫素值。當發生這種情況時，標準做法是簡單地將溢位的輸出畫素設定為最大允許值。通過使用支援範圍更大的畫素值的影象型別，可以避免此問題。

三、ARCore計算機視覺示例

  開啟ARCore SDK自帶的Computer vision示例。

  在Hierarchy視窗中選中ComputerVisionController，在Inspector視窗中雙擊編輯ComputerVisionController.cs指令碼。先不管其他輔助操作的功能如獲取攝像頭影象、顯示資訊等，我們直接檢視EdgeDetector.Detect()方法，這裡採用的邊緣檢測就是使用的Sobel運算元卷積。

       private static void Sobel(byte[] outputImage, IntPtr inputImage, int width, int height, int rowStride)
        {
            // Adjust buffer size if necessary.
            int bufferSize = rowStride * height;
            if (bufferSize != s_ImageBufferSize || s_ImageBuffer.Length == 0)
            {
                s_ImageBufferSize = bufferSize;
                s_ImageBuffer = new byte[bufferSize];
            }

            // Move raw data into managed buffer.
            System.Runtime.InteropServices.Marshal.Copy(inputImage, s_ImageBuffer, 0, bufferSize);

            // 邊緣檢測的閾值
            int threshold = 128 * 128;
            
            for (int j = 1; j < height - 1; j++)
            {
                for (int i = 1; i < width - 1; i++)
                {
                    // Offset of the pixel at [i, j] of the input image.
                    int offset = (j * rowStride) + i;

                    // Neighbour pixels around the pixel at [i, j].
                    int a00 = s_ImageBuffer[offset - rowStride - 1];
                    int a01 = s_ImageBuffer[offset - rowStride];
                    int a02 = s_ImageBuffer[offset - rowStride + 1];
                    int a10 = s_ImageBuffer[offset - 1];
                    int a12 = s_ImageBuffer[offset + 1];
                    int a20 = s_ImageBuffer[offset + rowStride - 1];
                    int a21 = s_ImageBuffer[offset + rowStride];
                    int a22 = s_ImageBuffer[offset + rowStride + 1];

                    int xSum = -a00 - (2 * a10) - a20 + a02 + (2 * a12) + a22;
                    int ySum = a00 + (2 * a01) + a02 - a20 - (2 * a21) - a22;
                    
                    if ((xSum * xSum) + (ySum * ySum) > threshold)
                    {
                        outputImage[(j * width) + i] = 0xFF;  //是邊緣則輸出純白
                    }
                    else
                    {
                        outputImage[(j * width) + i] = 0x1F;  //不是邊緣則輸出黑色
                    }
                }
            }
        }

  通過之前的講解，我們應該很容易理解這段程式碼，使用sobel運算元做邊緣檢測的效果如下圖所示：