為什麼要初始化？暴力初始化效果如何？

神經網路，或者深度學習演算法的引數初始化是一個很重要的方面，傳統的初始化方法從高斯分佈中隨機初始化引數。甚至直接全初始化為1或者0。這樣的方法暴力直接，但是往往效果一般。本篇文章的敘述來源於一個國外的討論帖子[1]，下面就自己的理解闡述一下。

首先我們來思考一下，為什麼在神經網路演算法（為了簡化問題，我們以最基本的DNN來思考）中，引數的選擇很重要呢？以sigmoid函式（logistic neurons）為例，當x的絕對值變大時，函式值越來越平滑，趨於飽和，這個時候函式的倒數趨於0，例如，在x=2時，函式的導數約為1/10，而在x=10時，函式的導數已經變成約為1/22000，也就是說，啟用函式的輸入是10的時候比2的時候神經網路的學習速率要慢2200倍！

為了讓神經網路學習得快一些，我們希望啟用函式sigmoid的導數較大。從數值上，大約讓sigmoid的輸入在[-4,4]之間即可，見上圖。當然，也不一定要那麼精確。我們知道，一個神經元j的輸入是由前一層神經元的輸出的加權和，。因此，我們可以通過控制權重引數初始值的範圍，使得神經元的輸入落在我們需要的範圍內，以便梯度下降能夠更快的進行。

先來看個例子。

在建立了神經網路後，通常需要對權重和偏置進行初始化，大部分的實現都是採取Gaussian distribution來生成隨機初始值。假設現在輸入層有1000個神經元，隱藏層有1個神經元，輸入資料x為一個全為1的1000維向量，採取高斯分佈來初始化權重矩陣w，偏置b取0。下面的程式碼計算隱藏層的輸入z：

然而通過上述初始化後，因為w服從均值為0、方差為1的正太分佈，x全為1，b全為0，輸入層一共1000個神經元，所以z服從的是一個均值為0、方差為1000的正太分佈。修改程式碼如下，生成20000萬個z並檢視其均值、方差以及分佈圖像：

輸出結果如下：

輸出影象如下：

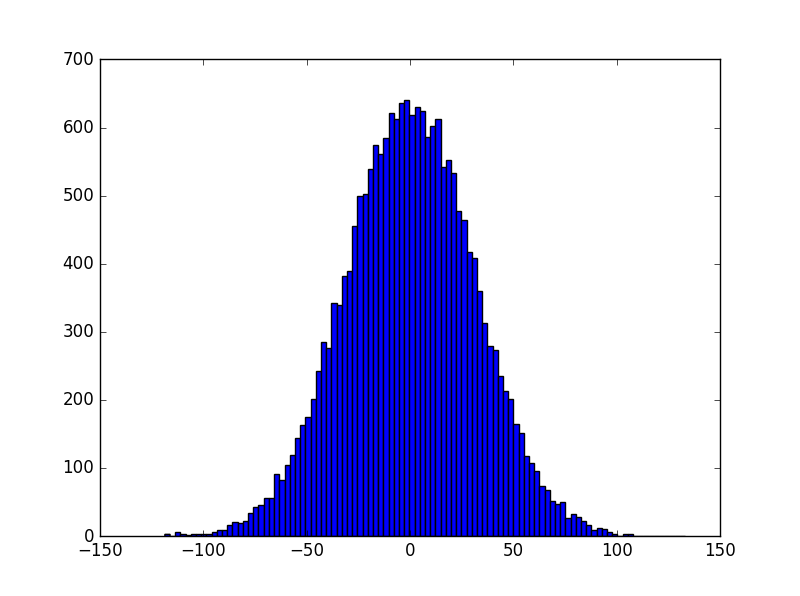
z分佈（1）

在此情況下，z有可能是一個遠小於-1或者遠大於1的數，通過啟用函式（比如sigmoid）後所得到的輸出會非常接近0或者1，也就是隱藏層神經元處於飽和的狀態。所以當出現這樣的情況時，在權重中進行微小的調整僅僅會給隱藏層神經元的啟用值帶來極其微弱的改變。

而這種微弱的改變也會影響網路中剩下的神經元，然後會帶來相應的代價函式的改變。結果就是，這些權重在我們進行梯度下降演算法時會學習得非常緩慢

因此，我們可以通過改變權重w的分佈，使|z|儘量接近於0 而不是使權重w接近0，如果x非常非常小，則權重應該稍微大點，這樣在正常的啟用函式下能夠分佈在0附近。這就是我們為什麼需要進行權重初始化的原因了。

權重初始化：How（取決於輸入x，以及啟用函式的特點，總的就是為了最後加權求和後更好的啟用）

一種簡單的做法是修改w的分佈，使得z服從均值為0、方差為1的標準正態分佈。根據正太分佈期望與方差的特性，將w除以sqrt(1000)即可。修改後程式碼如下：

輸出結果如下：

輸出影象如下：

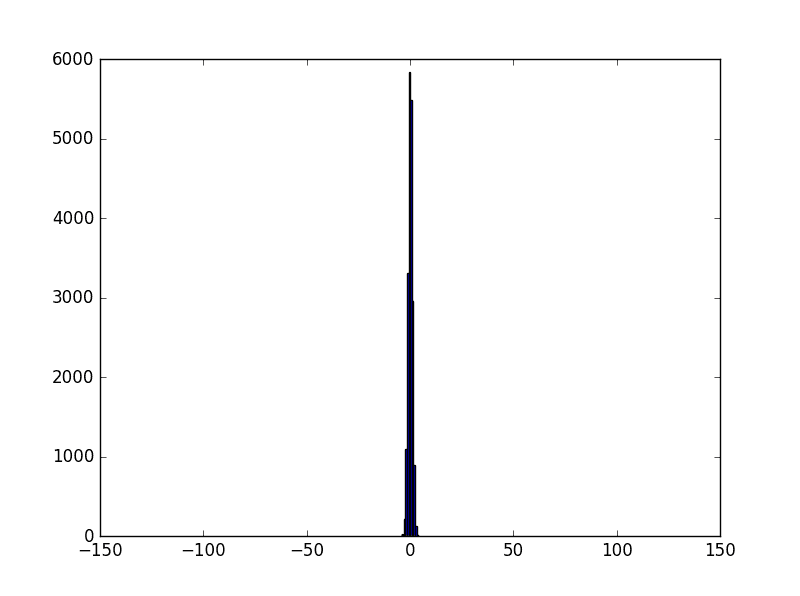
z分佈（2）

這樣的話z的分佈就是一個比較接近於0的數，使得神經元處於不太飽和的狀態，讓BP過程能夠正常進行下去。

除了這種方式之外（除以前一層神經元的個數n_in的開方），還有許多針對不同啟用函式的不同權重初始化方法，比如兼顧了BP過程的除以( (n_in + n_out)/2 )，還有初始化方法是截斷正態分佈，將權重在離均值兩個標準差外的值去掉。具體可以參考Stanford CS231n課程中提到的各種方法。

from：http://www.sohu.com/a/135067464_714863

        https://blog.csdn.net/qq_26898461/article/details/50996308