第十二週專案2 - 操作用鄰接表儲存的圖
/*Copyright (c) 2015, 煙臺大學計算機與控制工程學院
* All rights reserved.
* 檔名稱:H1.cpp
* 作者:辛志勐
* 完成日期:2015年11月20日
* 版本號:VC6.0
* 問題描述:操作用鄰接表儲存的圖
* 輸入描述:無
* 程式輸出:(1)輸出出圖G中每個頂點的出度;
(2)求出圖G中出度最大的一個頂點,輸出該頂點編號;
(3)計算圖G中出度為0的頂點數;
(4)判斷圖G中是否存在邊<i,j> 。
*/#include <stdio.h>
#include <malloc.h>
#define MAXV 100 //最大頂點個數
#define INF 32767 //INF表示∞
typedef int InfoType;
//以下定義鄰接矩陣型別
typedef struct
{
int no; //頂點編號
InfoType info; //頂點其他資訊,在此存放帶權圖權值
} VertexType; //頂點型別
typedef struct //圖的定義
{
int edges[MAXV][MAXV]; //鄰接矩陣
int n,e; //頂點數,弧數
VertexType vexs[MAXV]; //存放頂點資訊
} MGraph; //圖的鄰接矩陣型別
//以下定義鄰接表型別
typedef struct ANode //弧的結點結構型別
{
int adjvex; //該弧的終點位置
struct ANode *nextarc; //指向下一條弧的指標
InfoType info; //該弧的相關資訊,這裡用於存放權值
} ArcNode;
typedef int Vertex;
typedef struct Vnode //鄰接表頭結點的型別
{
Vertex data; //頂點資訊
int count; //存放頂點入度,只在拓撲排序中用
ArcNode *firstarc; //指向第一條弧
} VNode;
typedef VNode AdjList[MAXV]; //AdjList是鄰接表型別
typedef struct
{
AdjList adjlist; //鄰接表
int n,e; //圖中頂點數n和邊數e
} ALGraph; //圖的鄰接表型別
//功能:由一個反映圖中頂點鄰接關係的二維陣列,構造出用鄰接矩陣儲存的圖
//引數:Arr - 陣列名,由於形式引數為二維陣列時必須給出每行的元素個數,在此將引數Arr宣告為一維陣列名(指向int的指標)
// n - 矩陣的階數
// g - 要構造出來的鄰接矩陣資料結構
//void ArrayToMat(int *Arr, int n, MGraph &g); //用普通陣列構造圖的鄰接矩陣
void ArrayToList(int *Arr, int n, ALGraph *&); //用普通陣列構造圖的鄰接表
/*void MatToList(MGraph g,ALGraph *&G);//將鄰接矩陣g轉換成鄰接表G
void ListToMat(ALGraph *G,MGraph &g);//將鄰接表G轉換成鄰接矩陣g
void DispMat(MGraph g);//輸出鄰接矩陣g
void DispAdj(ALGraph *G);//輸出鄰接表G*/
//功能:由一個反映圖中頂點鄰接關係的二維陣列,構造出用鄰接矩陣儲存的圖
//引數:Arr - 陣列名,由於形式引數為二維陣列時必須給出每行的元素個數,在此將引數Arr宣告為一維陣列名(指向int的指標)
// n - 矩陣的階數
// g - 要構造出來的鄰接矩陣資料結構
/*void ArrayToMat(int *Arr, int n, MGraph &g)
{
int i,j,count=0; //count用於統計邊數,即矩陣中非0元素個數
g.n=n;
for (i=0; i<g.n; i++)
for (j=0; j<g.n; j++)
{
g.edges[i][j]=Arr[i*n+j]; //將Arr看作n×n的二維陣列,Arr[i*n+j]即是Arr[i][j],計算儲存位置的功夫在此應用
if(g.edges[i][j]!=0)
count++;
}
g.e=count;
}*/
void ArrayToList(int *Arr, int n, ALGraph *&G)
{
int i,j,count=0; //count用於統計邊數,即矩陣中非0元素個數
ArcNode *p;
G=(ALGraph *)malloc(sizeof(ALGraph));
G->n=n;
for (i=0; i<n; i++) //給鄰接表中所有頭節點的指標域置初值
G->adjlist[i].firstarc=NULL;
for (i=0; i<n; i++) //檢查鄰接矩陣中每個元素
for (j=n-1; j>=0; j--)
if (Arr[i*n+j]!=0) //存在一條邊,將Arr看作n×n的二維陣列,Arr[i*n+j]即是Arr[i][j]
{
p=(ArcNode *)malloc(sizeof(ArcNode)); //建立一個節點*p
p->adjvex=j;
p->info=Arr[i*n+j];
p->nextarc=G->adjlist[i].firstarc; //採用頭插法插入*p
G->adjlist[i].firstarc=p;
}
G->e=count;
}
/*void MatToList(MGraph g, ALGraph *&G)
//將鄰接矩陣g轉換成鄰接表G
{
int i,j;
ArcNode *p;
G=(ALGraph *)malloc(sizeof(ALGraph));G->n=g.n;
for (i=0; i<g.n; i++) //給鄰接表中所有頭節點的指標域置初值
G->adjlist[i].firstarc=NULL;
for (i=0; i<g.n; i++) //檢查鄰接矩陣中每個元素
for (j=g.n-1; j>=0; j--)
if (g.edges[i][j]!=0) //存在一條邊
{
p=(ArcNode *)malloc(sizeof(ArcNode)); //建立一個節點*p
p->adjvex=j;
p->info=g.edges[i][j];
p->nextarc=G->adjlist[i].firstarc; //採用頭插法插入*p
G->adjlist[i].firstarc=p;
}
G->e=g.e;
}
void ListToMat(ALGraph *G,MGraph &g)
//將鄰接表G轉換成鄰接矩陣g
{
int i,j;
ArcNode *p;
g.n=G->n; //根據一樓同學“舉報”改的。g.n未賦值,下面的初始化不起作用
g.e=G->e;
for (i=0; i<g.n; i++) //先初始化鄰接矩陣
for (j=0; j<g.n; j++)
g.edges[i][j]=0;
for (i=0; i<G->n; i++) //根據鄰接表,為鄰接矩陣賦值
{
p=G->adjlist[i].firstarc;
while (p!=NULL)
{
g.edges[i][p->adjvex]=p->info;
p=p->nextarc;
}
}
}
void DispMat(MGraph g)
//輸出鄰接矩陣g
{
int i,j;
for (i=0; i<g.n; i++)
{
for (j=0; j<g.n; j++)
if (g.edges[i][j]==INF)
printf("%3s","∞");
else
printf("%3d",g.edges[i][j]);
printf("\n");
}
}
void DispAdj(ALGraph *G)
//輸出鄰接表G
{
int i;
ArcNode *p;
for (i=0; i<G->n; i++)
{
p=G->adjlist[i].firstarc;
printf("%3d: ",i);
while (p!=NULL)
{
printf("-->%d/%d ",p->adjvex,p->info);
p=p->nextarc;
}
printf("\n");
}
}*/
int OutDegree(ALGraph *G,int v)
{
ArcNode *p;
int n=0;
p=G->adjlist[v].firstarc;
while (p!=NULL)
{
n++;
p=p->nextarc;
}
return n;
}
//輸出圖G中每個頂點的出度
void OutDs(ALGraph *G)
{
int i;
for (i=0; i<G->n; i++)
printf(" 頂點%d:%d\n",i,OutDegree(G,i));
}
//輸出圖G中出度最大的一個頂點
void OutMaxDs(ALGraph *G)
{
int maxv=0,maxds=0,i,x;
for (i=0; i<G->n; i++)
{
x=OutDegree(G,i);
if (x>maxds)
{
maxds=x;
maxv=i;
}
}
printf("頂點%d,出度=%d\n",maxv,maxds);
}
//輸出圖G中出度為0的頂點數
void ZeroDs(ALGraph *G)
{
int i,x;
for (i=0; i<G->n; i++)
{
x=OutDegree(G,i);
if (x==0)
printf("%2d",i);
}
printf("\n");
}
//返回圖G中是否存在邊<i,j>
bool Arc(ALGraph *G, int i,int j)
{
ArcNode *p;
bool found = false;
p=G->adjlist[i].firstarc;
while (p!=NULL)
{
if(p->adjvex==j)
{
found = true;
break;
}
p=p->nextarc;
}
return found;
}
int main()
{
ALGraph *G;
int A[7][7]=
{
{0,1,1,1,0,0,0},
{0,0,0,0,1,0,0},
{0,0,0,0,1,1,0},
{0,0,0,0,0,0,1},
{0,0,0,0,0,0,0},
{0,0,0,1,1,0,1},
{0,1,0,0,0,0,0}
};
ArrayToList(A[0], 7, G);
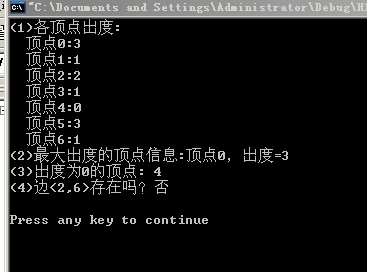
printf("(1)各頂點出度:\n");
OutDs(G);
printf("(2)最大出度的頂點資訊:");
OutMaxDs(G);
printf("(3)出度為0的頂點:");
ZeroDs(G);
printf("(4)邊<2,6>存在嗎?");
if(Arc(G,2,6))
printf("是\n");
else
printf("否\n");
printf("\n");
return 0;
}
知識點總結:鄰接矩陣的應用,運用迴圈實現。