C語言 inline行內函數與帶參巨集
C語言 inline行內函數與帶參巨集
一、簡述
簡單的介紹inline行內函數、帶參巨集的作用。
二、函式的執行與呼叫
函式執行:會將之前的棧的頂,棧基址壓棧,並在棧中開闢空間存放傳入的引數資料。返回時將返回資料放到通用暫存器,並釋放棧空間。
函式呼叫:在C語言中,程式式順序執行的,函式呼叫時,轉移到函式所存放的記憶體中的某個地址,將函式執行完之後,再返回到呼叫之前的位置,繼續執行。這種轉移再回來操作,要求在轉移之前保護現場(當時的執行狀態,如暫存器的值,程式執行到帶那裡,堆疊的使用情況等),在轉回之後要先恢復現場,然後繼續執行。
函式呼叫會增加時間和空間的開銷。頻繁的呼叫函式會影響程式的執行效率。
但是函式功能最好單一(一個函式一個功能),那麼有時候就需要將某一些程式碼功能封裝為函式模組,以方便多次呼叫,加上有意義的函式名簡潔易懂,方便維護。
三、帶參巨集
為了將某一部分程式碼功能封裝,但是又不想經過函式呼叫,我們可以使用帶參巨集來實現。
如:求最大值、最小值的函式
int Max(int x, int y) // 求兩個整數的最大值 { return (x>y?x:y); } int Min(int x, int y)// 求兩個整數的最小值 { return (x<y?x:y); }
如果在程式設計中多處需要求兩個數的最值,將其封裝成一個功能函式,讓程式碼更加的簡介,清晰,容易維護。
但是這個函式的程式碼量很少,多處呼叫,封裝成為函式就會花費時間和空間在函式呼叫上,會降低程式的執行效率。
在這種情況下,帶參巨集就能很好的解決:既能實現一定的封裝,又不會降低程式的執行效率。
將其編寫為帶參巨集:
#define MAX(x,y) (x>y?x:y)
#define MIN(x,y) (x<y?x:y)我們可以像函式一樣呼叫,但它不是函式,而是巨集,在預編譯階段就展開,其實就是簡單的替換。
如:
int a = 5;
int b = 8;
int c = Max(a, b);// 函式方式呼叫
int c = MAX(a, b);// 帶參巨集方式,在預編譯階段,這一句就會展開成為 int c = (a>b?a:b);
//其實就是簡單的巨集替換 將 MAX(a, b) 替換成為 (a>b?a:b)注1:C語言編從C程式碼譯成可執行檔案依次經過4個階段:預編譯、編譯、彙編、連結
預編譯:處理預編譯指令,如#include(檔案包含),#define(巨集替換),#if(條件編譯)等
編譯:將C程式碼編譯生成彙編程式碼
彙編:將彙編程式碼生成目標檔案(二進位制檔案)
連結:連結其他目標檔案、動態庫、靜態庫--》生成可執行檔案。
注2:巨集定義一般會將引數加小括號以確保優先順序(也就是無惡報按照自己的意願順序執行)
如:
#define MAX(x,y) (x>y?x:y) 會寫為 #define MAX(x,y) ( (x)>(y)?(x):(y) )舉例:不加小括號會出現的問題
// 以下定義一個求積的帶參巨集
#define MLT(x,y) x*y //或define MLT(x,y) (x*y)
//巨集一般使用大寫 multiplication:乘法
假設有
int a = 5;
int b = 8;
int c = MLT(a,b);// 等價 int c = a*b;可以正確得出結果
如果是
int c = MLT(a+2,b);// 等價int c = a+2*b 結果為21,與預期的(a+2)*b=(5+2)*8=56不同。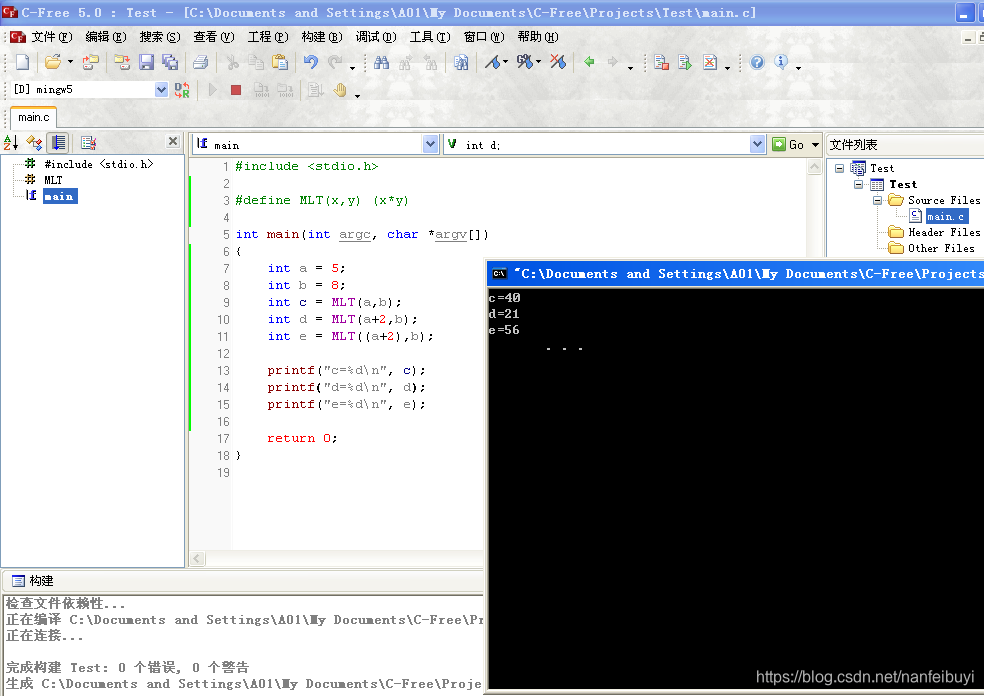
帶參巨集的優缺點:
優點:1) 在一定封裝性的同時提高執行效率。
2)可以簡單的實現"過載"。(對同一功能不同引數型別的相容)
缺點:1) 因為是純文字替換,不會進行引數型別檢查,並且容易出現優先順序問題。
2) 不方便除錯。
3) 如果呼叫的此時很多,那麼執行程式碼會增多。
四、行內函數 (inline)
在普通函式前面加上關鍵字inline,這個函式就稱為行內函數。如:
inline int Max(int x, int y) // 求兩個整數的最大值
{
return (x>y?x:y);
}行內函數在編譯時期展開,就是將 要呼叫的行內函數的程式碼 在呼叫的地方複製一份。這樣不用經過函式呼叫,提高執行效率。
行內函數的優缺點:
優點:1) 不用經過函式呼叫,提高執行效率。
2) 相對帶參巨集,在除錯程式時有更多有用的除錯資訊。
3) 進行引數型別檢查。
缺點:1) 最終由編譯器決定是否內聯,而且不能有遞迴,否則產生無窮展開。
2) 行內函數的使用可能大大增加編譯時間。
3) 如果多處呼叫,會增加程式碼量。
五、總結
無論是帶參巨集,函式行內函數,都有著"減少函式呼叫,提高執行效率"的目的。並且都有著"簡潔的封裝"的意思。
所以想要將某一動作作為帶參巨集或者是行內函數,這個動作最好要"簡單"一點,最好不要有多層巢狀的迴圈,不要有遞迴呼叫。
巨集:簡單的純文字替換(在預編譯階段展開)。
行內函數:將函式程式碼複製到要呼叫的地方(在編譯階段展開)。
