整合演算法(Bagging,隨機森林)
引言(關於整合學習)
整合演算法包括很多種包括Bagging,隨機森林,Boosting 以及其他更加高效的整合演算法。在這篇部落格上只介紹Bagging演算法及隨機森林,Boosting提升演算法及其他高效的演算法在下一篇詳細講解。
整合演算法就是通過構建多個學習器來完成學習任務,是由多個基學習器或者是個體學習器來完成的。它可以是由決策樹,神經網路等多種基學習演算法組成。就像是投票表決答案一樣,多數人的參與總會比一個人的觀點更加準確。整合學習通過多個學習器進行結合,可以獲得比單一學習器顯著優越的泛化效能。而且整合學習一般都是以弱學習器整合來得到一個強的學習器獲得更好地效能。
假設整合通過簡單的投票方法結合T個基分類器,如果其中有半數基分類器正確,則整合分類就正確:
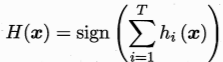
假設基分類器錯誤率相互獨立 ,由Hoeffding不等式可知,整合的錯誤率為:
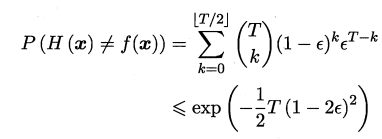
可以看出隨著整合中個體分類器數目T的的增加整合的錯誤率將指數級下降最終趨向於零。前提是有一個關鍵假設:基學習器的誤差相互獨立。 我們所要選擇的基學習器就是要選擇那些好而不同個體學習器,如何去選擇他們就是整合學習的核心內容。
Bagging(bootstrap aggregation)
Bootstraping的名稱來自於成語 ‘’pull up by your own bootstraps‘’, 意思是依靠你自己的資源,稱為自助法,它是一種有放回的抽樣方法。Bootstrap的本意是指高靴子後面的懸掛物,小環,是穿鞋子時用手向上拉的工具。意思是不可能的事情後來意思發生了轉變,隱喻 ‘’不需要外界幫助,僅依靠自身力量讓自己變得更好‘’。
Bagging策略
對資料進行自助取樣法,對結果進行簡單投票法。 對於給定的包含m個樣本的資料集,我們隨機選擇一個樣本放入取樣集中,再把該樣本放回初始資料集,使得下次取樣仍有可能被選中。我們這樣選擇的樣本有的在取樣集裡面重複出現,有的則從未出現。我們分類任務使用簡單投票法;對分類任務使用簡單平均法;若分類投票出現相同的票數情況,則隨機選擇一個。

Bagging 演算法

Bagging演算法是一種很高效的一種演算法,但是也具有一定的侷限性,他不能經修改的適用於多分類和迴歸等任務。
隨機森林(Random Forest,簡稱RF)
隨機森林是Bagging的一個擴充套件變體,RF在以決策樹為基學習器構建Bagging整合的基礎上,進一步在決策樹的訓練過程中映入了隨機屬性選擇。具體來說,傳統的決策樹在選擇劃分屬性時在當前節點選擇一個最優屬性;而在RF中對基決策樹的每個節點,先從該節點的屬性集合中隨機選擇一個包含k個屬性的子集,然後再從這個子集中選擇一個最優屬性用於劃分。在很多例子中表現功能強大,進一步使泛化效能提升,被稱為 ‘代表整合學習技術水平的方法’。

隨機森林在Bagging的基礎上做了修改
- 從樣本集中用Bootstrap取樣選出n個樣本;
- 從所有屬性中隨機選擇k個屬性,選擇最佳分割屬性作為節點建立CART決策樹;
- 重複以上兩個步驟m次,即建立了m棵CART決策樹
- 這m棵CART決策樹形成隨機森林,通過投票表決結果,決定資料屬於哪一類
隨機森林、Bagging和決策樹的關係
- 可以使用決策樹作為基本分類器
- 也可以使用SVM,Logistic迴歸等其他分類器,習慣上,這些分類器組成的 ‘’總分類器‘’,仍然叫做隨機森林。
投票機制
簡單投票機制
- 一票否決
- 少數服從多數
相對多數投票法:如果同時多個標記獲得最高票,冊隨機選擇一個
- 加權投票法
- 閾值表決
貝葉斯投票機制
學習法
訓練資料很多時,我們另一通過另一個學習器來進行結合,模型融合也會用到。具體參考 Stacking
小結
決策樹隨機森林的程式碼清晰,邏輯也是比較簡單,在勝任分類問題時,往往可以作為對資料分類探索的首要嘗試方法,隨機森林的整合思想方法也可以用在其他分類器的設計中。
