每日一題之 Splay (伸展樹)
描述
小Ho:小Hi,上一次你跟我講了Treap,我也實現了。但是我遇到了一個關鍵的問題。
小Hi:怎麼了?
小Ho:小Hi你也知道,我平時運氣不太好。所以這也反映到了我寫的Treap上。
小Hi:你是說你隨機出來的權值不太好,從而導致結果很差麼?
小Ho:就是這樣,明明一樣的程式碼,我的Treap執行結果總是不如別人。小Hi,有沒有那種沒有隨機因素的平衡樹呢?
小Hi:當然有了,這次我就跟你講講一種叫做Splay的樹吧。而且Splay樹能做到的功能比Treap要更強大哦。
小Ho:那太好了,你快告訴我吧!
提示:Splay
輸入
第1行:1個正整數n,表示運算元量,100≤n≤200,000
第2…n+1行:可能包含下面3種規則:
1個字母’I’,緊接著1個數字k,表示插入一個數字k到樹中,1≤k≤1,000,000,000,保證每個k都不相同
1個字母’Q’,緊接著1個數字k。表示詢問樹中不超過k的最大數字
1個字母’D’,緊接著2個數字a,b,表示刪除樹中在區間[a,b]的數。
輸出
若干行:每行1個整數,表示針對詢問的回答,保證一定有合法的解
樣例輸入
6
I 1
I 2
I 3
Q 4
D 2 2
Q 2
樣例輸出
3
1
思路:
小Hi:Splay樹,中文名一般叫做伸展樹。
和Treap樹相同,作為平衡樹,它也是通過左旋和右旋來調整樹的結構。
這裡我們再複習一下左旋和右旋操作:
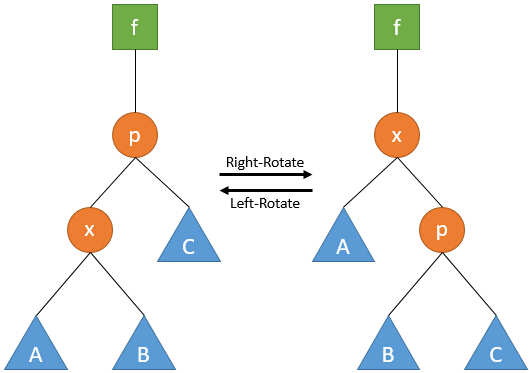
若以x作為引數(注意上一講中是以p作為引數),其對應的虛擬碼分別為:
right-rotate(x):
p = x.father
x.father = p.father
If (p.father is not empty) Then
If (p.father.left == p) Then
p.father.left = x
Else
p.father.right = x
End If
Else
root = x
End If
p.left = x.right
x.right.father = p
x.right = p
p.father = 和Treap樹不同的是,Splay樹不再用一個隨機的權值來進行平衡,而是用固定的調整方式來使得調整之後的樹會比較平衡。
在左旋右旋的基礎上,Splay樹定義了3個操作:
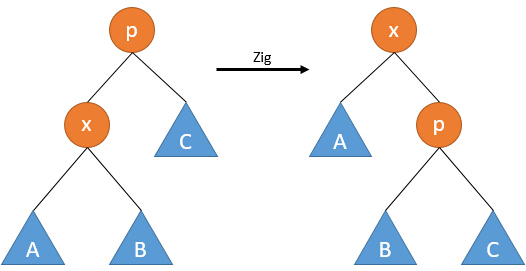
2.jpg
直接根據x節點的位置,進行左旋或右旋。
該操作將x節點提升了一層。
- Zig-Zig
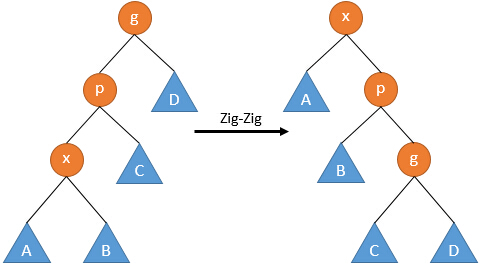
若p不是根節點,還有父親節點g,且p和x同為左兒子或右兒子,則進行Zig-Zig操作:
當x,p同為左兒子時,依次將p和x右旋;
當x,p同為右兒子時,依次將p和x左旋。
注意此處不是將x連續Zig兩次。該操作將x節點提升了兩層。
- Zig-Zag
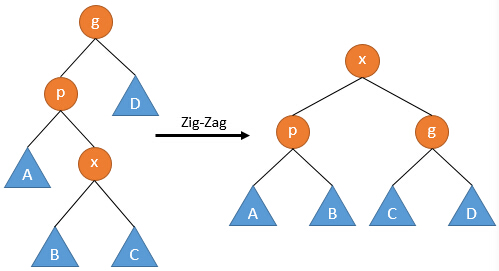
若p不是根節點,則p還有父親節點g。且p和x不同為左兒子或右兒子,則進行Zig-Zag操作:
當p為左兒子,x為右兒子時,將x節點先左旋再右旋;
當p為右兒子,x為左兒子時,將x節點先右旋再左旋。
該操作將x節點提升了兩層。
進一步在Zig,Zig-Zig和Zig-Zag操作上,Splay樹定義了"Splay"操作。
對於x以及x的祖先y,splay(x, y),表示對x節點進行調整,使得x是y的兒子節點:
splay(x, y):
While (x.father != y)
p = x.father
If (p.father == y) Then
// 因為p的父親是y,所以只需要將x進行Zig操作
// 就可以使得x的父親變為y
If (p.left == x) Then
right-rotate(x)
Else
left-rotate(x)
End If
Else
g = p.father
If (g.left == p) Then
If (p.left == x) Then
// x,p同為左兒子,Zig-Zig操作
right-rotate(p)
right-rotate(x)
Else
// p為左,x為右,Zig-Zag操作
left-rotate(x)
right-rotate(x)
End If
Else
If (p.right == x) Then
// x,p同為右兒子,Zig-Zig操作
left-rotate(p)
left-rotate(x)
Else
// p為右,x為左,Zig-Zag操作
right-rotate(x)
left-rotate(x)
End If
End If
End If
End While
在執行這個操作的時候,需要保證y節點一定是x節點祖先。
值得一提的是,大多數情況下我們希望通過splay操作將x旋轉至整棵樹的根節點。此時只需令y=NULL即可實現。
小Ho:旋轉和Splay我懂了,但是要怎麼運用上去呢?
小Hi:Splay樹的插入和查詢操作和普通的二叉搜尋樹沒有什麼大的區別,需要注意的是每次插入和查詢結束後,需要對訪問節點做一次Splay操作,將其旋轉至根。
insert(key):
node = bst_insert(key) // 同普通的BST插入, node為當前插入的新節點
splay(node, NULL)
find(key):
node = bst_find(key) // 同普通的BST查詢, node為查詢到的節點
splay(node, NULL)
同時由於Splay的特性,我們還有兩個特殊的查詢操作。在樹中查詢指定數key的前一個數和後一個數。
我們先將key旋轉至根,那麼key的前一個數一定是根節點左兒子的最右子孫,同時key的後一個數一定是根節點右兒子的最左子孫。
findPrev(key):
splay( find(key), NULL )
node = root.left
While (node.right)
node = node.right
Return node
findNext(key):
splay( find(key), NULL )
node = root.right
While (node.left)
node = node.left
Return node
splay中的刪除key操作:
splay的刪除可以採用和一般二叉搜尋樹相同的方法:即先找到節點key,若key沒有兒子則直接刪去;若key有1個兒子,則用兒子替換掉x;若key有2個兒子,則通過找到其前(或後)一個節點來替換掉它,最後將該節點Splay到根。
同時,這裡還有另一種方法來完成刪除操作:
首先我們查詢到key的前一個數prev和後一個數next。將prev旋轉至根,再將next旋轉為prev的兒子。
此時key節點一定是next的左兒子。那麼直接將next的左兒子節點刪去即可。
delete(key):
prev = findPrev(key)
next = findNext(key)
splay(prev, NULL)
splay(next, prev)
next.left = NULL
這裡你可能會擔心如果key是數中最小或者是最大的數怎麼辦?
一個簡單的處理方式是手動加入一個超級大和超級小的值作為頭尾。
那麼小Ho,這裡有一個問題,假如要刪除一個區間[a,b]的數該怎麼做?
小Ho:我想想…我知道了!
因為要刪除[a,b],那麼我就要想辦法把[a,b]的數旋轉到一個子樹上,再將這個子樹刪掉就行了。
方法和刪除一個數相同,我首先將a的前一個數prev和b的後一個數next找出來。
同樣將prev旋轉至根,再將next旋轉為prev的兒子。
那麼此時next的左子樹一定就是所有[a,b]之間的數了!
deleteInterval(a, b):
prev = findPrev(a)
next = findNext(b)
splay(prev, NULL)
splay(next, prev)
next.left = NULL
小Hi:沒錯,那麼下一個問題!如果a,b不在樹中呢?
小Ho:這還不簡單,把a,b插入樹中,做完之後再刪除不就好了!
小Hi:想不到小Ho你還蠻機智的嘛。
小Ho:那是,畢竟是我小Ho。(哼哼)
小Hi:Splay樹由於splay操作的使得其相較於Treap具有更大的靈活性,並且不再有隨機性。其插入、查詢和刪除操作的均攤時間複雜度也都是O(logn)的,具體的複雜度分析可以參考這裡。那麼最後小Ho你能夠把Splay的實現出來麼?
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e9+7;
const int minn = -1;
struct Splay {
int key;
Splay* left;
Splay* right;
Splay* father;
Splay(int x){
key = x;
left = nullptr;
right = nullptr;
father = nullptr;
}
};
Splay* root;
void rightRotate(Splay* x) {
Splay* p = x->father;
x->father = p->father;
if (p->father != nullptr) {
if (p->father->left == p)
p->father->left = x;
else
p->father->right = x;
}
else {
root = x;
}
p->left = x->right;
if (x->right != nullptr)
x->right->father = p;
x->right = p;
p->father = x;
}
void leftRotate(Splay* x) {
Splay* p = x->father;
x->father = p->father;
if (p->father != nullptr) {
if (p->father->left == p)
p->father->left = x;
else
p->father->right = x;
}
else {
root = x;
}
p->right = x->left;
if (x->left != nullptr)
x->left->father = p;
x->left = p;
p->father = x;
}
void splay(Splay* x, Splay* y) {
if (x == nullptr) return;
Splay* p = nullptr;
Splay* g = nullptr;
while(x->father != y) {
p = x->father;
//cout <<"-1" << endl;
if (p->father == y) {//因為p的父親是y,所以只需要將x進行
//zig操作就可以使得x的父親變為y
if (p->left == x)
rightRotate(x);
else
leftRotate(x);
}
else {
g = p->father;
if (g->left == p) {
if (p->left == x) {
//x,p同為左兒子,Zig-Zig操作
rightRotate(p);
rightRotate(x);
}
else { //p為左,x為右,Zig-Zag操作
leftRotate(x);
rightRotate(x);
}
}
else {
if (p->right == x) {
//x,p同為右兒子,Zig-Zig操作
leftRotate(p);
leftRotate(x);
}
else {
//p為右,x為左Zig-Zag操作
rightRotate(x);
leftRotate(x);
}
}
}
}
}
Splay* Insert(Splay* node, int key) {
if (key < node->key) {
if (node->left == nullptr) {
Splay* tmp = new Splay(key);
node->left = tmp;
tmp->father = node;
return node->left;
}
else {
return Insert(node->left, key);
}
}
else {
if (node->right == nullptr) {
Splay* tmp = new Splay(key);
node->right = tmp;
tmp->father = node;
return node->right;
}
else {
return Insert(node->right, key);
}
}
}
void spalyInsert(int key) {
if (root == nullptr) {
root = new Splay(key);
}
else{
Splay* node = Insert(root, key);
splay(node, nullptr);
}
}
Splay* Find(Splay* cur, int key) {
if (cur == nullptr) return nullptr;
if (cur->key == key) {
return cur;
}
if (key < cur->key) {
return Find(cur->left, key);
}
else
return Find(cur->right, key);
}
void splayFind(int key) {
Splay* node = Find(root, key);
splay(node, nullptr);
}
Splay* findPrev(int key) {
Splay* node;
splayFind(key);
node = root->left;
while(node->right != nullptr) {
node = node->right;
}
return node;
}
Splay* findNext(int key) {
Splay* node;
splayFind(key);
node = root->right;
while(node->left != nullptr) {
node = node->left;
}
return node;
}
void Delete(int key) {
Splay* prev;
Splay* Next;
prev = findPrev(key);
Next = findNext(key);
splay(prev, nullptr);
splay(Next, prev);
Next->left = nullptr;
}
void visit(Splay* cur) {
if (cur) {
cout << cur->key<< " ";
visit(cur->left);
visit(cur->right);
}
}
void deleteInterval(int a, int b) {
Splay* prev;
Splay* Next;
Splay* aa = Find(root, a);
if (aa == nullptr) spalyInsert(a);
prev = findPrev(a);
Splay* bb = Find(root, b);
if (bb == nullptr) spalyInsert(b);
Next = findNext(b);
splay(prev, nullptr);
splay(Next, prev);
Next->left = nullptr;
}
void Search(Splay* cur, int x, int &res) {
if (cur == nullptr) return;
if (cur->key == x) {
res = x;
return;
}
if (cur->key > x) {
Search(cur->left, x, res);
}
else {
res = cur->key;
Search(cur->right, x, res);
}
}
void solve(int n) {
char op;
int x, y, res = 0;
root = nullptr;
spalyInsert(maxn);
spalyInsert(minn);
for (int i = 0; i < n; ++i) {
cin >> op >> x;
if (op == 'I') {
spalyInsert(x);
}
else if (op == 'Q') {
//int res;
Search(root, x, res);
cout << res << endl;
}
else if (op == 'D'){
cin >> y;
//spalyInsert(x);
//spalyInsert(y);
deleteInterval(x, y);
}
}
}
int main() {
int n;
cin >> n;
solve(n);
return 0;
}
簡便寫法
同樣利用STL中的set,程式碼變得非常簡單
#include <cstdio>
#include <set>
#include <cstring>
#include <iostream>
using namespace std;
set<int> s;
void solve(int n) {
char op;
int x, y;
set<int>::iterator it;
for (int i = 0; i < n; ++i) {
cin >> op >> x;
if (op == 'I') {
s.insert(x);
}
else if (op == 'Q') {
it = s.upper_bound(x);
--it;
cout << *it << endl;
}
else if (op == 'D'){
cin >> y;
it = s.lower_bound(x);
while(it != s.end() && *it <= y) {
s.erase(it++);
}
}
}
}
int main(){
int n;
cin >> n;
solve(n);
return 0;
}
