在學習了普通二叉排序樹的演算法之後，我們發現了它的一些不足，如果我們的普通二叉樹在插入資料的時候造成樹的一側資料過多的話，就會使得查詢的時候效率大大降低，在極端情況下，我們插入一串有序的數，原本的二叉樹就會變成連結串列，例如，插入：1，2，3，4，5，6，結果就會變成下圖這樣：

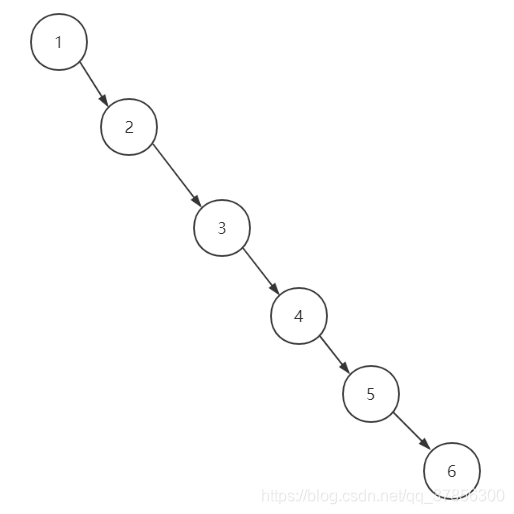
這樣就違背了我們二叉樹的初衷，相當於有一邊的孩子節點失去了意義，這種二叉樹就是不平衡的二叉樹。
那麼具體什麼樣的二叉樹是不平衡的二叉樹呢？
我們規定，如果一個樹節點的左孩子節點高度和右孩子節點高度的差大於等於2，則這個節點就是不平衡的節點，同時這個差值叫做這個節點的平衡因子。
也就是說，如果一個節點的平衡因子絕對值大於等於2了，這個節點就失衡了。

1.左單旋操作

我們發現，右子樹比左子樹高度差達到2了，形象地來說，現在右邊的樹枝太重了，樹不平衡了。如果變成下圖這樣就會平衡了：

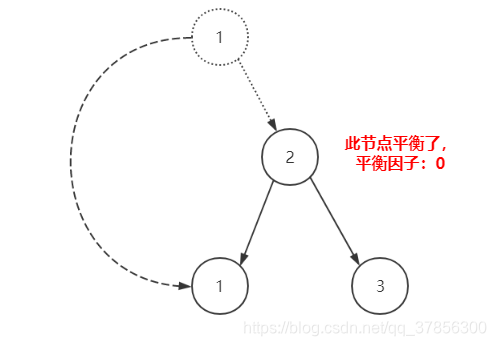
這裡，我們稱為對結點1做了左單旋操作。

2.右單旋操作

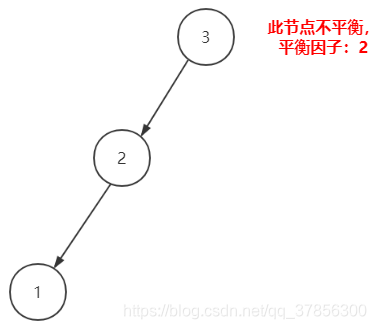
我們發現，左子樹比右子樹高度差達到2了，樹不平衡了。如果變成下圖這樣就會平衡了：

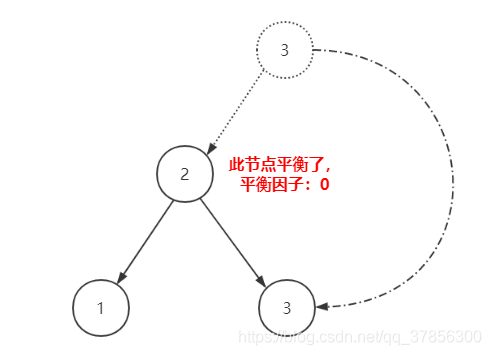
這裡，我們稱為對結點3做了右單旋操作。

3.先右旋再左旋

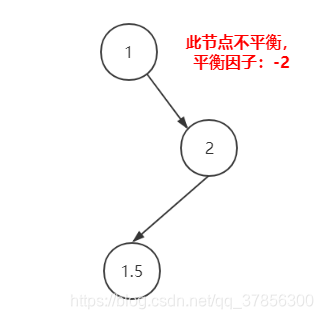
對於這種情況，我們需要通過兩步將它變為平衡：

1.先對2節點進行右旋

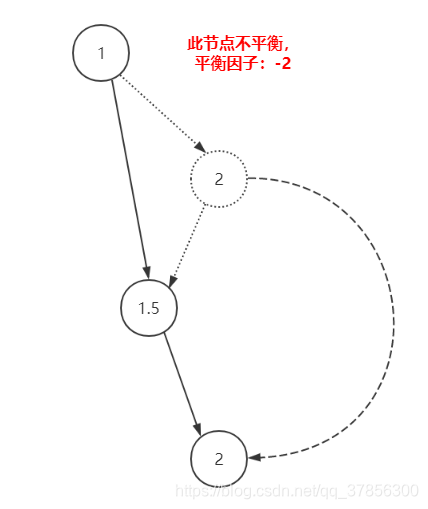
2.再對1節點進行左旋

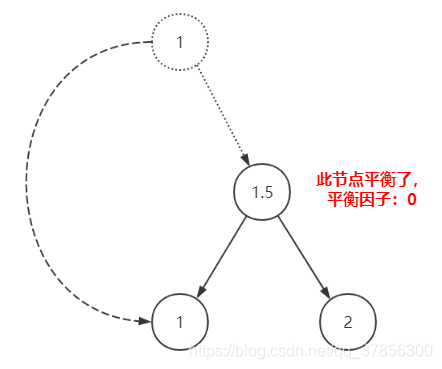
4.先左旋再右旋

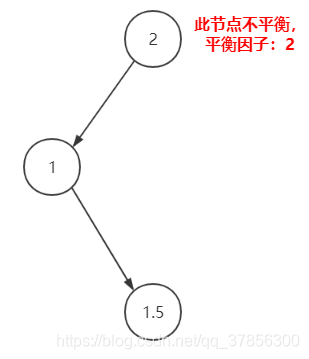
1.先對1節點進行左旋

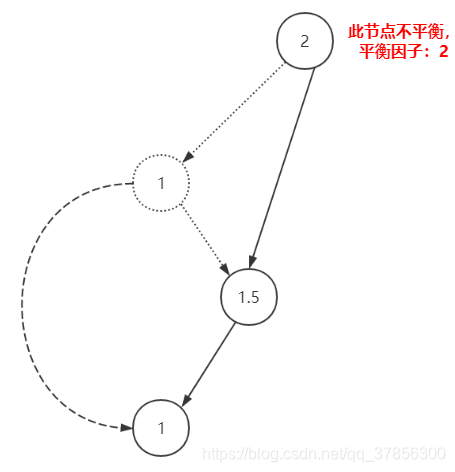
2.再對2節點進行右旋

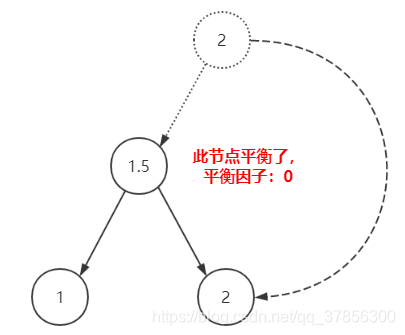
至此，我們已經說完了各種基本操作，現在讓我們來看程式碼：
樹的結構：

public class Tree {
	public Tree leftChild;
	public Tree rightChild;
	public int data;//記錄節點的資料
	public int height;//用來記錄節點的高度
}

基本操作：

public static Tree rightRotate(Tree root)//右單旋
	{ // root為失衡的樹點，也就是平衡因子的絕對值大於等於2的點
        Tree temp = root.
 
leftChild;
        root.leftChild = temp.rightChild; // 將失衡點root的左孩子temp的右子樹成為失衡點p的左子樹
        temp.rightChild = root; // 將失衡點作為temp的右子樹
        // 重新調整失衡點及其左孩子節點的高度值(只有這兩個節點的高度值可能發生改變)
        root.height = Math.max(getHeight(root.leftChild), getHeight(root.rightChild)) + 1;
        temp.height = Math.max(getHeight(temp.leftChild), root.height) + 1;
        return temp; // 失衡點root的左孩子成為新的根節點(取代原失衡點的位置)
    }
	 public static Tree leftRotate(Tree root)//左單旋
	 {
        Tree temp = root.rightChild;
        root.rightChild = temp.leftChild; // 將失衡點root的右孩子temp的左子樹成為失衡點root的右子樹
        temp.leftChild = root; // 將失衡點root作為temp左子樹
        // 重新調整失衡點及其右孩子節點的高度值
        root.height = Math.max(getHeight(root.leftChild), getHeight(root.rightChild)) + 1;
        temp.height = Math.max(getHeight(temp.leftChild), getHeight(temp.rightChild)) + 1;
        return temp; //  失衡點root的右孩子成為新的根節點(取代原失衡點的位置)
    }
	 public static Tree leftAndRight(Tree root)//先左旋再右旋
	 {
		 root.leftChild=leftRotate(root.leftChild);//先以失衡點root的左孩子作為根節點進行左旋
		 return rightRotate(root);//再以失衡點root作為根節點進行右旋
	 }
	 public static Tree rightAndLeft(Tree root)//先右旋再左旋
	 {
		 root.rightChild=rightRotate(root.rightChild);//先以失衡點root的右孩子作為根節點進行右旋
		 return leftRotate(root);//再以失衡點root作為根節點進行左旋
	 }
	 public static Tree findNextNode(Tree root)//找到右子樹下最小的節點
	 {
        if(root == null)
        {
            return null;
        }
        Tree r = root.rightChild;
        while(r != null && r.leftChild != null)
        {
            r = r.leftChild;
        }
        return r;
	 }

插入：

public static Tree insert(Tree root, int data) 
	 {
        if (root == null) //如果到的根節點為null，那麼就在此處插入那個新的節點，用來終止遞迴
        {
            root = new Tree();
            root.data=data;
            return root;
        }
        if (data <= root.data) 
        { 
            root.leftChild = insert(root.leftChild, data);// 如果要插的值小於或等於當前的節點值，插入進其左子樹
            if (getHeight(root.leftChild) - getHeight(root.rightChild) > 1) //當平衡因子大於等於2時
            { // 由於是向當前root樹的左邊插入，所以左子樹高度必定不小於右子樹高度
                if (data <= root.leftChild.data) 
                { // 最後插入的葉子結點在該root樹的左孩子的左邊
                    root = rightRotate(root); // 右旋，然後將調整後的root返回給其父節點的左子樹域
                }
                else
                { // 最後插入的葉子結點在該root樹的左孩子的右邊
                    root = leftAndRight(root);// 先左旋再右旋，然後將調整後的root返回給其父節點的左子樹域
                }
            }
        }
        else
        { 
            root.rightChild = insert(root.rightChild, data);// 如果要插的值大於當前的節點值，插入進其右子樹
            if(getHeight(root.rightChild) - getHeight(root.leftChild) > 1)
            {
                if(data <= root.rightChild.data)
                {
                    root = rightAndLeft(root);// 先右旋再左旋，然後將調整後的root返回給其父節點的右子樹域
                }
                else
                {
                    root = leftRotate(root);// 左旋，然後將調整後的root返回給其父節點的右子樹域
                }
            }
        }
        // 當插入新的節點後，從這個節點到根節點的最短路徑上的節點的高度值一定會發生改變，另外當出現失衡點時，這個失衡點的所有祖先節點的高度值也可能會發生改變
        root.height = Math.max(getHeight(root.leftChild), getHeight(root.rightChild)) + 1; // 重新調整root節點的高度值
        return root;
    }

刪除：

public static Tree remove(Tree root, int data)
	 {
	        if(root == null)
	        { // 沒有找到刪除的節點
	            return null;
	        }
	        if(data < root.data)
	        { // 在左子樹上刪除
	            root.leftChild = remove(root.leftChild, data);
	            if(getHeight(root.rightChild) - getHeight(root.leftChild) > 1)
	            { // 在左子樹上刪除，右子樹高度一定不小於左子樹高度
	                if(getHeight(root.rightChild.leftChild) > getHeight(root.rightChild.rightChild))
	                {
	                    root = rightAndLeft(root);
	                }
	                else
	                {
	                    root = leftRotate(root);
	                }
	            }
	        }
	        else if(data == root.data)
	        { // 找到刪除的節點
	            if(root.leftChild != null && root.rightChild != null)
	            { // 刪除的節點既有左子樹又有右子樹
	                root.data = findNextNode(root).data; // 將失衡點的data域更改為其直接後繼節點的data域
	                root.rightChild = remove(root.rightChild, root.data); // 將問題轉換為刪除其直接後繼節點
	            }else
	            { // 只有左子樹或者只有右子樹或者為葉子結點的情況
	                root = (root.leftChild == null) ? root.rightChild : root.leftChild;
	            }
	        }
	        else
	        { // 在root的右子樹上查詢刪除節點
	            root.rightChild = remove(root.rightChild, data);
	            if(getHeight(root.leftChild) - getHeight(root.rightChild) > 1)
	            {
	                if(getHeight(root.leftChild.leftChild) > getHeight(root.leftChild.rightChild))
	                {
	                    root = rightRotate(root);
	                }
	                else
	                {
	                    root = leftAndRight(root);
	                }
	            }
	        }
	        if(root != null)
	        { // 更新root的高度值
	            root.height = Math.max(getHeight(root.leftChild), getHeight(root.rightChild)) + 1;
	        }
	        return root;
	    }