GradientBoosting和AdaBoost實現MNIST手寫體數字識別
一、兩種演算法簡介:
Boosting 演算法簡介
Boosting演算法,我理解的就是兩個思想:
1)“三個臭皮匠頂個諸葛亮”,一堆弱分類器的組合就可以成為一個強分類器;
2)“知錯能改,善莫大焉”,不斷地在錯誤中學習,迭代來降低犯錯概率
當然,要理解好Boosting的思想,首先還是從弱學習演算法和強學習演算法來引入:
1)強學習演算法:存在一個多項式時間的學習演算法以識別一組概念,且識別的正確率很高;
2)弱學習演算法:識別一組概念的正確率僅比隨機猜測略好;
Kearns & Valiant證明了弱學習演算法與強學習演算法的等價問題,如果兩者等價,只需找到一個比隨機猜測略好的學習演算法,就可以將其提升為強學習演算法。
那麼是怎麼實現“知錯就改”的呢?
Boosting演算法,通過一系列的迭代來優化分類結果,每迭代一次引入一個弱分類器,來克服現在已經存在的弱分類器組合的shortcomings
在Adaboost演算法中,這個shortcomings的表徵就是權值高的樣本點
而在Gradient Boosting演算法中,這個shortcomings的表徵就是梯度
無論是Adaboost還是Gradient Boosting,都是通過這個shortcomings來告訴學習器怎麼去提升模型,也就是“Boosting”這個名字的由來吧
Adaboost演算法
Adaboost是由Freund 和 Schapire在1997年提出的,在整個訓練集上維護一個分佈權值向量W,用賦予權重的訓練集通過弱分類演算法產生分類假設(基學習器)y(x),然後計算錯誤率,用得到的錯誤率去更新分佈權值向量w,對錯誤分類的樣本分配更大的權值,正確分類的樣本賦予更小的權值。每次更新後用相同的弱分類演算法產生新的分類假設,這些分類假設的序列構成多分類器。對這些多分類器用加權的方法進行聯合,最後得到決策結果。
其結構如下圖所示:
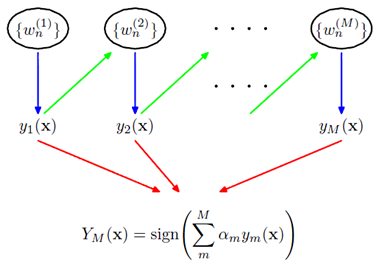
前一個學習器改變權重w,然後再經過下一個學習器,最終所有的學習器共同組成最後的學習器。
如果一個樣本在前一個學習器中被誤分,那麼它所對應的權重會被加重,相應地,被正確分類的樣本的權重會降低。
這裡主要涉及到兩個權重的計算問題:
1)樣本的權值
1> 沒有先驗知識的情況下,初始的分佈應為等概分佈,樣本數目為n,權值為1/n
2> 每一次的迭代更新權值,提高分錯樣本的權重
2)弱學習器的權值
1> 最後的強學習器是通過多個基學習器通過權值組合得到的。
2> 通過權值體現不同基學習器的影響,正確率高的基學習器權重高。實際上是分類誤差的一個函式
Gradient Boosting
和Adaboost不同,Gradient Boosting 在迭代的時候選擇梯度下降的方向來保證最後的結果最好。
損失函式用來描述模型的“靠譜”程度,假設模型沒有過擬合,損失函式越大,模型的錯誤率越高
如果我們的模型能夠讓損失函式持續的下降,則說明我們的模型在不停的改進,而最好的方式就是讓損失函式在其梯度方向上下降。
下面這個流程圖是Gradient Boosting的經典圖了,數學推導並不複雜,只要理解了Boosting的思想,不難看懂

這裡是直接對模型的函式進行更新,利用了引數可加性推廣到函式空間。
訓練F0-Fm一共m個基學習器,沿著梯度下降的方向不斷更新ρm和am
GradientBoostingRegressor實現
python中的scikit-learn包提供了很方便的GradientBoostingRegressor和GBDT的函式介面,可以很方便的呼叫函式就可以完成模型的訓練和預測
GradientBoostingRegressor函式的引數如下:
class sklearn.ensemble.GradientBoostingRegressor(loss='ls', learning_rate=0.1, n_estimators=100, subsample=1.0, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_depth=3, init=None, random_state=None, max_features=None, alpha=0.9, verbose=0, max_leaf_nodes=None, warm_start=False, presort='auto')[source]¶
loss: 選擇損失函式,預設值為ls(least squres)
learning_rate: 學習率,模型是0.1
n_estimators: 弱學習器的數目,預設值100
max_depth: 每一個學習器的最大深度,限制迴歸樹的節點數目,預設為3
min_samples_split: 可以劃分為內部節點的最小樣本數,預設為2
min_samples_leaf: 葉節點所需的最小樣本數,預設為1
……
可以參考 http://scikit-learn.org/stable/modules/generated/sklearn.ensemble.GradientBoostingRegressor.html
官方文件裡帶了一個很好的例子,以500個弱學習器,最小平方誤差的梯度提升模型,做波士頓房價預測,程式碼和結果如下:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import ensemble
from sklearn import datasets
from sklearn.utils import shuffle
from sklearn.metrics import mean_squared_error
###############################################################################
# Load data
boston = datasets.load_boston()
X, y = shuffle(boston.data, boston.target, random_state=13)
X = X.astype(np.float32)
offset = int(X.shape[0] * 0.9)
X_train, y_train = X[:offset], y[:offset]
X_test, y_test = X[offset:], y[offset:]
###############################################################################
# Fit regression model
params = {'n_estimators': 500, 'max_depth': 4, 'min_samples_split': 1,
'learning_rate': 0.01, 'loss': 'ls'}
clf = ensemble.GradientBoostingRegressor(**params)
clf.fit(X_train, y_train)
mse = mean_squared_error(y_test, clf.predict(X_test))
print("MSE: %.4f" % mse)
###############################################################################
# Plot training deviance
# compute test set deviance
test_score = np.zeros((params['n_estimators'],), dtype=np.float64)
for i, y_pred in enumerate(clf.staged_predict(X_test)):
test_score[i] = clf.loss_(y_test, y_pred)
plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.title('Deviance')
plt.plot(np.arange(params['n_estimators']) + 1, clf.train_score_, 'b-',
label='Training Set Deviance')
plt.plot(np.arange(params['n_estimators']) + 1, test_score, 'r-',
label='Test Set Deviance')
plt.legend(loc='upper right')
plt.xlabel('Boosting Iterations')
plt.ylabel('Deviance')
###############################################################################
# Plot feature importance
feature_importance = clf.feature_importances_
# make importances relative to max importance
feature_importance = 100.0 * (feature_importance / feature_importance.max())
sorted_idx = np.argsort(feature_importance)
pos = np.arange(sorted_idx.shape[0]) + .5
plt.subplot(1, 2, 2)
plt.barh(pos, feature_importance[sorted_idx], align='center')
plt.yticks(pos, boston.feature_names[sorted_idx])
plt.xlabel('Relative Importance')
plt.title('Variable Importance')
plt.show()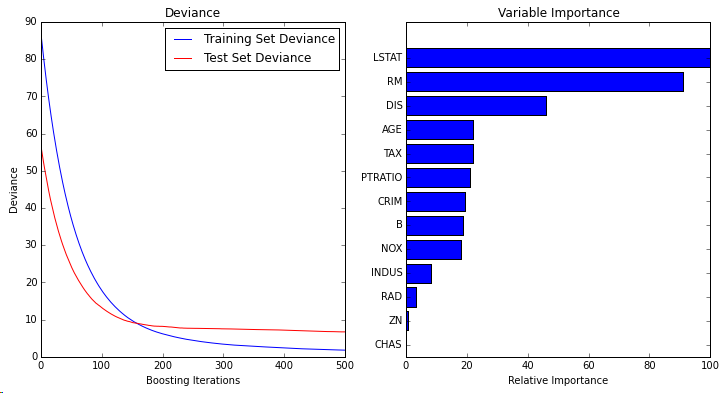
可以發現,如果要用Gradient Boosting 演算法的話,在sklearn包裡呼叫還是非常方便的,幾行程式碼即可完成,大部分的工作應該是在特徵提取上。
二、MNIST測試:
# -*- coding: utf-8 -*-
# @Time : 2018/8/21 10:32
# @Author : Barry
# @File : mnist_GB.py
# @Software: PyCharm Community Edition
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.metrics import accuracy_score
import tensorflow.examples.tutorials.mnist.input_data as input_data
import time
from datetime import datetime
data_dir = '../MNIST_data/'
mnist = input_data.read_data_sets(data_dir,one_hot=False)
batch_size = 50000
batch_x,batch_y = mnist.train.next_batch(batch_size)
test_x = mnist.test.images[:10000]
test_y = mnist.test.labels[:10000]
print("start Gradient Boosting")
StartTime = time.clock()
for i in range(10,200,10):
clf_rf = GradientBoostingClassifier(n_estimators=i)
clf_rf.fit(batch_x,batch_y)
y_pred_rf = clf_rf.predict(test_x)
acc_rf = accuracy_score(test_y,y_pred_rf)
print("%s n_estimators = %d, random forest accuracy:%f" % (datetime.now(), i, acc_rf))
EndTime = time.clock()
print('Total time %.2f s' % (EndTime - StartTime))結果:
start Gradient Boosting
2018-08-22 09:39:53.114800 n_estimators = 10, random forest accuracy:0.845200
2018-08-22 09:46:25.680700 n_estimators = 20, random forest accuracy:0.883500
2018-08-22 09:56:21.176710 n_estimators = 30, random forest accuracy:0.902800
2018-08-22 10:09:17.453814 n_estimators = 40, random forest accuracy:0.917600
2018-08-22 10:25:45.233702 n_estimators = 50, random forest accuracy:0.925600
2018-08-22 10:45:38.344716 n_estimators = 60, random forest accuracy:0.929900
2018-08-22 11:09:17.834999 n_estimators = 70, random forest accuracy:0.935100
2018-08-22 11:36:38.280471 n_estimators = 80, random forest accuracy:0.939500
2018-08-22 12:06:21.974137 n_estimators = 90, random forest accuracy:0.942200
2018-08-22 12:40:35.648684 n_estimators = 100, random forest accuracy:0.944300
2018-08-22 13:17:52.943346 n_estimators = 110, random forest accuracy:0.947300
2018-08-22 14:00:00.915921 n_estimators = 120, random forest accuracy:0.948600
2018-08-22 14:47:46.923277 n_estimators = 130, random forest accuracy:0.950300
2018-08-22 15:41:09.575049 n_estimators = 140, random forest accuracy:0.952400
2018-08-22 16:38:04.491657 n_estimators = 150, random forest accuracy:0.954200
2018-08-22 17:38:36.862459 n_estimators = 160, random forest accuracy:0.955000
2018-08-22 18:42:45.162086 n_estimators = 170, random forest accuracy:0.956600
2018-08-22 19:51:19.596696 n_estimators = 180, random forest accuracy:0.957500mnist_AB.py
# -*- coding: utf-8 -*-
# @Time : 2018/8/21 10:39
# @Author : Barry
# @File : mnist_AB.py
# @Software: PyCharm Community Edition
from sklearn.ensemble import AdaBoostClassifier
from sklearn.metrics import accuracy_score
import tensorflow.examples.tutorials.mnist.input_data as input_data
import time
from datetime import datetime
data_dir = '../MNIST_data/'
mnist = input_data.read_data_sets(data_dir,one_hot=False)
batch_size = 50000
batch_x,batch_y = mnist.train.next_batch(batch_size)
test_x = mnist.test.images[:10000]
test_y = mnist.test.labels[:10000]
print("start Gradient Boosting")
StartTime = time.clock()
for i in range(10,200,10):
clf_rf = AdaBoostClassifier(n_estimators=i)
clf_rf.fit(batch_x,batch_y)
y_pred_rf = clf_rf.predict(test_x)
acc_rf = accuracy_score(test_y,y_pred_rf)
print("%s n_estimators = %d, random forest accuracy:%f" % (datetime.now(), i, acc_rf))
EndTime = time.clock()
print('Total time %.2f s' % (EndTime - StartTime))執行結果:
start Gradient Boosting
2018-08-22 19:47:39.340555 n_estimators = 10, random forest accuracy:0.590400
2018-08-22 19:48:06.411962 n_estimators = 20, random forest accuracy:0.692200
2018-08-22 19:48:45.641367 n_estimators = 30, random forest accuracy:0.692800
2018-08-22 19:49:34.456253 n_estimators = 40, random forest accuracy:0.710300
2018-08-22 19:50:38.019661 n_estimators = 50, random forest accuracy:0.717800
2018-08-22 19:51:56.216605 n_estimators = 60, random forest accuracy:0.730200
2018-08-22 19:53:21.201670 n_estimators = 70, random forest accuracy:0.734600
2018-08-22 19:54:58.991348 n_estimators = 80, random forest accuracy:0.735000
2018-08-22 19:56:51.498537 n_estimators = 90, random forest accuracy:0.728900
2018-08-22 19:59:01.355309 n_estimators = 100, random forest accuracy:0.733200
2018-08-22 20:01:11.853150 n_estimators = 110, random forest accuracy:0.720400
2018-08-22 20:03:34.914754 n_estimators = 120, random forest accuracy:0.707800
2018-08-22 20:06:12.198900 n_estimators = 130, random forest accuracy:0.711600
2018-08-22 20:09:07.673904 n_estimators = 140, random forest accuracy:0.711800
2018-08-22 20:12:14.946045 n_estimators = 150, random forest accuracy:0.719700
2018-08-22 20:15:34.760213 n_estimators = 160, random forest accuracy:0.722100三、小結
Adaboost演算法執行比Gradientboost演算法執行更快! 但是從準確度上來看,梯度提升演算法效果更好。
