演算法：拓撲排序

拓撲排序

什麼是拓撲排序

　　其實在寫這篇部落格的時候，我也是以一個學習者的角度出發的，目的就是想讓自己理解和初步掌握拓撲排序。

　　維基百科的定義如下：　　

　　　　在電腦科學領域，有向圖頂點的線性排序就是其拓撲排序，例如，圖形的頂點可以表示要執行的任務，並且邊可以表示一個任務必須在另一個任務之前執行的約束; 在這個應用中，拓撲排序只是一個有效的任務順序。當且僅當圖形沒有定向迴圈，即如果它是有向無環圖（DAG），則拓撲排序是可能的。 任何 DAG 具有至少一個拓撲排序，並且已知這些演算法用於線上性時間內構建任何 DAG 的拓撲排序。

　　在圖論中，由一個有向無環圖的頂點組成的序列，當且僅當滿足下列條件時，稱為該圖的一個拓撲排序

1. 每個頂點出現且只出現一次；
2. 若存在一條從頂點 A 到頂點 B 的路徑，那麼在序列中頂點 A 出現在頂點 B 的前面。

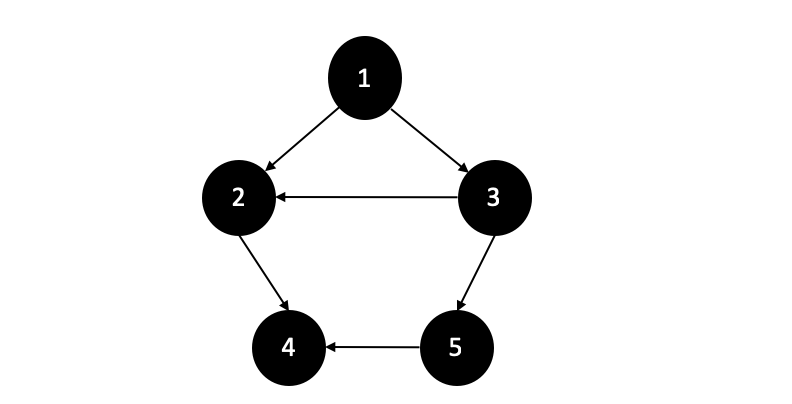
　　比如在下圖中，當然首先必須是有向無環圖，從1出發到達，拓撲序列可以為1,3,2,5,4。

我們在寫有向無環圖的拓撲排序時遵循一種常用的方法：

1. 從 DAG 圖中選擇一個 沒有前驅（即入度為0）的頂點並輸出。
2. 從圖中刪除該頂點和所有以它為起點的有向邊。
3. 重複 1 和 2 直到當前的 DAG 圖為空或當前圖中不存在無前驅的頂點為止。後一種情況說明有向圖中必然存在環。

拓撲排序的應用

　　拓撲排序通常用來“排序”具有依賴關係的任務。

　　比如，如果用一個DAG圖來表示一個工程，其中每個頂點表示工程中的一個任務，用有向邊 表示在做任務 B 之前必須先完成任務 A。故在這個工程中，任意兩個任務要麼具有確定的先後關係，要麼是沒有關係，絕對不存在互相矛盾的關係（即環路）。

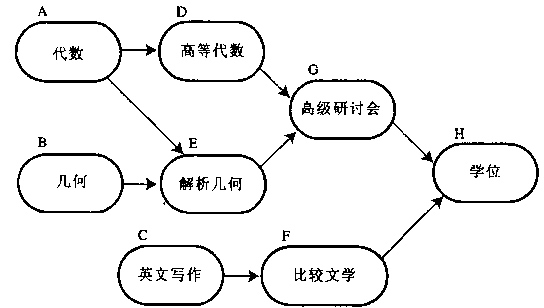
拓撲排序的實現

演算法圖解