目錄

• 1.讀取原始影象
• 2.網格劃分，將影象劃分為m*n塊
• 2.1分塊後圖像的儲存問題
• 2.2影象的裁剪
• 2.3影象長寬的整除問題
• 方法一：四捨五入法
• 方法二：影象縮放法
• 3.顯示分塊後的影象
• 4.分塊影象的還原
• 5.參考文獻

1.讀取原始影象

import numpy as np 
import matplotlib.pyplot as plt 
import cv2

img = cv2.imread('cat.jpg')
img = cv2.cvtColor(img,cv2.COLOR_BGR2RGB)

h, w = img.
 
shape[0], img.shape[1]
fig1 = plt.figure('原始影象')
plt.imshow(img)
plt.axis('off')
plt.title('Original image')
print( '\t\t\t   原始影象形狀:\n', '\t\t\t',img.shape ) 

2.網格劃分，將影象劃分為m*n塊

  這裡有三個要點：影象的儲存問題，影象的裁剪方法，長寬不能整除的問題。下面逐一介紹

2.1分塊後圖像的儲存問題

  由於事先不知道m和n的具體值，因此也就不知道影象的分塊數目具體是多少個。必須想個辦法來儲存這 $m \times n$個影象分塊，建立 $m \times n$個變數來儲存也是不可取的，因為這樣會讓程式變得很複雜。
  本人想到一個很簡單的方法：增加維度的方法。建立一個五維的張量來存放各個劃分後的子影象塊，其中前面兩維表示該影象塊在原影象的位置（如第i行第j列的分塊），後面三個維度表示每個子影象塊的具體內容(R、G、B的值)。

2.2影象的裁剪

  直接利用numpy的切片功能將每個網格的左上角和右下角的座標值所確定的影象塊的畫素直接寫入五維張量即可。這裡只需要注意網格頂點座標的確認，在處理的時候橫座標和縱座標對應的維度不要搞反。

2.3影象長寬的整除問題

  上一步還存在一個很大的bug：如果影象的長寬不能分別被m和n整除就會帶來網格點非整數的問題，還會帶來部分影象分塊的大小與其他影象分塊不一致的問題。舉個例子，比如我的影象尺寸是 $3 \times 3$，現在要把這個影象分成 $1 \times 2$個影象塊，那麼第2列畫素就要一分為二才能做到真正的均勻劃分，這顯然是不可能的。

方法一：四捨五入法

  我們做個簡單的處理，直接對網格頂點的座標進行四捨五入取整，這樣一來，第2個畫素就被劃分到左邊的分塊了，但是這樣會帶來一個新的問題，即每個影象塊的大小不一致。還沿用前面的例子，尺寸為 $3 \times 3$會被劃分為 $3 \times 2$和 $3 \times 1$兩個影象塊，這會導致影象分塊的不均勻，也會導致前面的五維張量不合理。一般來說，我們要分塊的影象都是很大的，而劃分的塊數一般不會特別多，所以舍入誤差帶來的幾個畫素的差異完全可以忽略，針對這種情況，一個比較好的思路就是在五維張量的填充中只對已知位置的畫素進行填充，而把其他位置的畫素值仍然設定為0。
完整程式為：

def divide_method1(img,m,n):#分割成m行n列
    h, w = img.shape[0],img.shape[1]
    gx=np.round(gx).astype(np.int)
    gy=np.round(gy).astype(np.int)

    divide_image = np.zeros([m-1, n-1, int(h*1.0/(m-1)+0.5), int(w*1.0/(n-1)+0.5),3], np.uint8)#這是一個五維的張量，前面兩維表示分塊後圖像的位置（第m行，第n列），後面三維表示每個分塊後的影象資訊
    for i in range(m-1):
        for j in range(n-1):      
            divide_image[i,j,0:gy[i+1][j+1]-gy[i][j], 0:gx[i+1][j+1]-gx[i][j],:]= img[
                gy[i][j]:gy[i+1][j+1], gx[i][j]:gx[i+1][j+1],:]#這樣寫比a[i,j,...]=要麻煩，但是可以避免網格分塊的時候，有些影象塊的比其他影象塊大一點或者小一點的情況引起程式出錯
    return divide_image

方法二：影象縮放法

  這個方法很簡單，將影象縮放一下，讓其滿足整除關係即可。

def divide_method2(img,m,n):#分割成m行n列
    h, w = img.shape[0],img.shape[1]
    grid_h=int(h*1.0/(m-1)+0.5)#每個網格的高
    grid_w=int(w*1.0/(n-1)+0.5)#每個網格的寬
    
    #滿足整除關係時的高、寬
    h=grid_h*(m-1)
    w=grid_w*(n-1)
    
    #影象縮放
    img_re=cv2.resize(img,(w,h),cv2.INTER_LINEAR)# 也可以用img_re=skimage.transform.resize(img, (h,w)).astype(np.uint8)
    #plt.imshow(img_re)
    gx, gy = np.meshgrid(np.linspace(0, w, n),np.linspace(0, h, m))
    gx=gx.astype(np.int)
    gy=gy.astype(np.int)

    divide_image = np.zeros([m-1, n-1, grid_h, grid_w,3], np.uint8)#這是一個五維的張量，前面兩維表示分塊後圖像的位置（第m行，第n列），後面三維表示每個分塊後的影象資訊
    
    for i in range(m-1):
        for j in range(n-1):      
            divide_image[i,j,...]=img_re[
            gy[i][j]:gy[i+1][j+1], gx[i][j]:gx[i+1][j+1],:]
    return divide_image

3.顯示分塊後的影象

def display_blocks(divide_image):#    
    m,n=divide_image.shape[0],divide_image.shape[1]
    for i in range(m):
        for j in range(n):
            plt.subplot(m,n,i*n+j+1)
            plt.imshow(divide_image[i,j,:])
            plt.axis('off')
            plt.title('block:'+str(i*n+j+1))

方法一：四捨五入法

m=3
n=4
divide_image1=divide_method1(img,m+1,n+1)#該函式中m+1和n+1表示網格點個數，m和n分別表示分塊的塊數
fig2 = plt.figure('分塊後的子影象:四捨五入法')
display_blocks(divide_image1)

方法二：影象縮放法

divide_image2=divide_method2(img,m+1,n+1)#該函式中m+1和n+1表示網格點個數，m和n分別表示分塊的塊數
fig3 = plt.figure('分塊後的子影象:影象縮放法')
display_blocks(divide_image2)

4.分塊影象的還原

主要目的是將分塊後的影象拼接起來，還原成一幅完整的大影象。有兩個方法：
　　1.使用opencv。其實opencv自帶的有影象拼接的函式，hconcat函式：用於兩個Mat矩陣或者影象的水平拼接；vconcat函式：用於兩個Mat矩陣或者影象的垂直拼接。
　　2.自己動手寫。影象拼接是影象分塊的逆過程，首先建立一個空的還原後的影象，然後將對於位置填充上對應的畫素即可。
　　由於事先不知道具體分成多少塊，使用opencv拼接影象是很麻煩的。為了簡單，我們還是選擇第２種方法，自己動手豐衣足食！

def image_concat(divide_image):
    m,n,grid_h, grid_w=[divide_image.shape[0],divide_image.shape[1],#每行，每列的影象塊數
                       divide_image.shape[2],divide_image.shape[3]]#每個影象塊的尺寸

    restore_image = np.zeros([m*grid_h, n*grid_w, 3], np.uint8)
    restore_image[0:grid_h,0:]
    for i in range(m):
        for j in range(n):
            restore_image[i*grid_h:(i+1)*grid_h,j*grid_w:(j+1)*grid_w]=divide_image[i,j,:]
    return restore_image

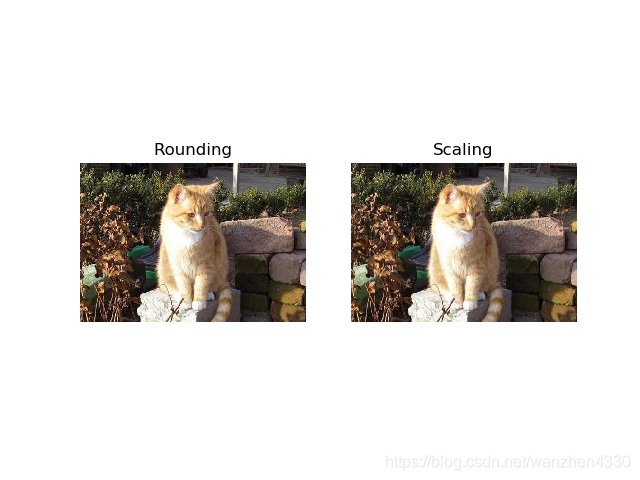
下面分別顯示‘四捨五入法’和‘影象縮放法’得到的分塊影象的還原結果。

fig4 = plt.figure('分塊影象的還原')
restore_image1=image_concat(divide_image1)#四捨五入法分塊還原
restore_image2=image_concat(divide_image2)#影象縮放法分塊還原
plt.subplot(1,2,1)
plt.imshow(restore_image1)
plt.axis('off')
plt.title('Rounding')
plt.subplot(1,2,2)
plt.imshow(restore_image2)
plt.axis('off')
plt.title('Scaling')
print('\t\t\t還原後的影象尺寸')
print('\t‘四捨五入法’：', restore_image1.shape,'\t''‘影象縮放法’：', restore_image2.shape)
plt.show()

5.參考文獻

[1]影象的水平方向或者垂直方向拼接https://blog.csdn.net/mangobar/article/details/79656417