Calculate distance, bearing and more between Latitude/Longitude points
原文地址:http://www.movable-type.co.uk/scripts/latlong.html
Movable Type Scripts
Calculate distance, bearing and more between Latitude/Longitude points
This page presents a variety of calculations for latitude/longitude points, with the formulæ and code fragments for implementing them.
All these formulæ are for calculations on the basis of a spherical earth (ignoring ellipsoidal effects) – which is accurate enough
Distance
This uses the ‘haversine’ formula to calculate the great-circle distance between two points – that is, the shortest distance over the earth’s surface – giving an ‘as-the-crow-flies’ distance between the points (ignoring any hills they fly over, of course!).
| Haversine formula: |
a = sin²(Δφ/2) + cos φ1 ⋅ cos φ2 ⋅ sin²(Δλ/2) c = 2 ⋅ atan2( √a, √(1−a) ) d = R ⋅ c |
| where | φ is latitude, λ is longitude, R is earth’s radius (mean radius = 6,371km); note that angles need to be in radians to pass to trig functions! |
| JavaScript: | var R = 6371; // km
var φ1 = lat1.toRadians();
var φ2 = lat2.toRadians();
var Δφ = (lat2-lat1).toRadians();
var Δλ = (lon2-lon1).toRadians();
var a = Math.sin(Δφ/2) * Math.sin(Δφ/2) +
Math.cos(φ1) * Math.cos(φ2) *
Math.sin(Δλ/2) * Math.sin(Δλ/2);
var c = 2 * Math.atan2(Math.sqrt(a), Math.sqrt(1-a));
var d = R * c; |
Note in these scripts, I generally use lat/lon for latitude/longitude in degrees, and φ/λ for latitude/longitude in radians – having found that mixing degrees & radians is often the easiest route to head-scratching bugs...
Historical aside: The height of technology for navigator’s calculations used to be log tables. As there is no (real) log of a negative number, the ‘versine’ enabled them to keep trig functions in positive numbers. Also, the sin²(θ/2) form of the haversine avoided addition (which entailed an anti-log lookup, the addition, and a log lookup). Printedtables for the haversine/inverse-haversine (and its logarithm, to aid multiplications) saved navigators from squaring sines, computing square roots, etc – arduous and error-prone activities.
The haversine formula1 ‘remains particularly well-conditioned for numerical computation even at small distances’ – unlike calculations based on thespherical law of cosines. The ‘versed sine’ is 1−cosθ, and the ‘half-versed-sine’ is (1−cosθ)/2 = sin²(θ/2) as used above. Once widely used by navigators, it was described by Roger Sinnott in Sky & Telescope magazine in 1984 (“Virtues of the Haversine”): Sinnott explained that the angular separation between Mizar and Alcor in Ursa Major – 0°11′49.69″ – could be accurately calculated on a TRS-80 using the haversine.
For the curious, c is the angular distance in radians, and a is the square of half the chord length between the points. A (remarkably marginal) performance improvement can be obtained by factoring out the terms which get squared.
Spherical Law of Cosines
In fact, JavaScript (and most modern computers & languages) use ‘IEEE 754’ 64-bit floating-point numbers, which provide 15 significant figures of precision. By my estimate, with this precision, the simple spherical law of cosines formula (cos c = cos a cos b + sin a sin b cos C) gives well-conditioned results down to distances as small as a few metres on the earth’s surface. (Note that the geodetic form of the law of cosines is rearranged from the canonical one so that the latitude can be used directly, rather than the colatitude).
This makes the simpler law of cosines a reasonable 1-line alternative to the haversine formula for many geodesy purposes (if not for astronomy). The choice may be driven by coding context, available trig functions (in different languages), etc – and, for very small distances an equirectangular approximation may be more suitable.
| Law of cosines: | d = acos( sin φ1 ⋅ sin φ2 + cos φ1 ⋅ cos φ2 ⋅ cos Δλ ) ⋅ R |
| JavaScript: | var φ1 = lat1.toRadians(), φ2 = lat2.toRadians(), Δλ = (lon2-lon1).toRadians(), R = 6371; // gives d in km var d = Math.acos( Math.sin(φ1)*Math.sin(φ2) + Math.cos(φ1)*Math.cos(φ2) * Math.cos(Δλ) ) * R; |
| Excel: | =ACOS( SIN(lat1)*SIN(lat2) + COS(lat1)*COS(lat2)*COS(lon2-lon1) ) * 6371 |
| (or with lat/lon in degrees): | =ACOS( SIN(lat1*PI()/180)*SIN(lat2*PI()/180) + COS(lat1*PI()/180)*COS(lat2*PI()/180)*COS(lon2*PI()/180-lon1*PI()/180) ) * 6371 |
Equirectangular approximation
If performance is an issue and accuracy less important, for small distances Pythagoras’ theorem can be used on anequirectangular projection:*
| Formula | x = Δλ ⋅ cos φm y = Δφ d = R ⋅ √x² + y² |
| JavaScript: | var x = (λ2-λ1) * Math.cos((φ1+φ2)/2); var y = (φ2-φ1); var d = Math.sqrt(x*x + y*y) * R; |
This uses just one trig and one sqrt function – as against half-a-dozen trig functions for cos law, and 7 trigs + 2 sqrts for haversine. Accuracy is somewhat complex: along meridians there are no errors, otherwise they depend on distance, bearing, and latitude, but are small enough for many purposes* (and often trivial compared with the spherical approximation itself).
Alternatively, the polar coordinate flat-earth formula can be used: using the co-latitudes θ1 = π/2−φ1 and θ2 = π/2−φ2, then d = R ⋅ √θ1² + θ2² − 2 ⋅ θ1 ⋅ θ2 ⋅ cos Δλ. I’ve not compared accuracy.
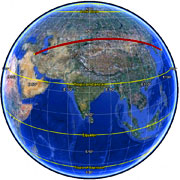 Baghdad to Osaka –
Baghdad to Osaka –
not a constant bearing!
Bearing
In general, your current heading will vary as you follow a great circle path (orthodrome); the final heading will differ from the initial heading by varying degrees according to distance and latitude (if you were to go from say 35°N,45°E (≈ Baghdad) to 35°N,135°E (≈ Osaka), you would start on a heading of 60° and end up on a heading of 120°!).
This formula is for the initial bearing (sometimes referred to as forward azimuth) which if followed in a straight line along a great-circle arc will take you from the start point to the end point:1
| Formula: | θ = atan2( sin Δλ ⋅ cos φ2 , cos φ1 ⋅ sin φ2 − sin φ1 ⋅ cos φ2 ⋅ cos Δλ ) |
| JavaScript:
(all angles
in radians) |
var y = Math.sin(λ2-λ1) * Math.cos(φ2);
var x = Math.cos(φ1)*Math.sin(φ2) -
Math.sin(φ1)*Math.cos(φ2)*Math.cos(λ2-λ1);
var brng = Math.atan2(y, x).toDegrees(); |
| Excel:
(all angles
in radians) |
=ATAN2(COS(lat1)*SIN(lat2)-SIN(lat1)*COS(lat2)*COS(lon2-lon1), SIN(lon2-lon1)*COS(lat2)) *note that Excel reverses the arguments to ATAN2 – see notes below |
Since atan2 returns values in the range -π ... +π (that is, -180° ... +180°), to normalise the result to a compass bearing (in the range 0° ... 360°, with −ve values transformed into the range 180° ... 360°), convert to degrees and then use (θ+360) % 360, where % is (floating point) modulo.
For final bearing, simply take the initial bearing from the end point to the start point and reverse it (using θ = (θ+180) % 360).
Midpoint
This is the half-way point along a great circle path between the two points.1
| Formula: | Bx = cos φ2 ⋅ cos Δλ By = cos φ2 ⋅ sin Δλ φm = atan2( sin φ1 + sin φ2, √(cos φ1 + Bx)² + By² ) λm = λ1 + atan2(By, cos(φ1)+Bx) |
| JavaScript:
(all angles
in radians) |
var Bx = Math.cos(φ2) * Math.cos(λ2-λ1);
var By = Math.cos(φ2) * Math.sin(λ2-λ1);
var φ3 = Math.atan2(Math.sin(φ1) + Math.sin(φ2),
Math.sqrt( (Math.cos(φ1)+Bx)*(Math.cos(φ1)+Bx) + By*By ) );
var λ3 = λ1 + Math.atan2(By, Math.cos(φ1) + Bx); |
Just as the initial bearing may vary from the final bearing, the midpoint may not be located half-way between latitudes/longitudes; the midpoint between 35°N,45°E and 35°N,135°E is around 45°N,90°E.
Destination point given distance and bearing from start point
Given a start point, initial bearing, and distance, this will calculate the destination point and final bearing travelling along a (shortest distance) great circle arc.
| Formula: | φ2 = asin( sin φ1 ⋅ cos δ + cos φ1 ⋅ sin δ ⋅ cos θ ) |
| λ2 = λ1 + atan2( sin θ ⋅ sin δ ⋅ cos φ1, cos δ − sin φ1 ⋅ sin φ2 ) | |
| where | φ is latitude, λ is longitude, θ is the bearing (clockwise from north), δ is the angular distance d/R; d being the distance travelled, R the earth’s radius |
| JavaScript:
(all angles
in radians) |
var φ2 = Math.asin( Math.sin(φ1)*Math.cos(d/R) +
Math.cos(φ1)*Math.sin(d/R)*Math.cos(brng) );
var λ2 = λ1 + Math.atan2(Math.sin(brng)*Math.sin(d/R)*Math.cos(φ1),
Math.cos(d/R)-Math.sin(φ1)*Math.sin(φ2)); |
| Excel:
(all angles
in radians) |
lat2: =ASIN(SIN(lat1)*COS(d/R) + COS(lat1)*SIN(d/R)*COS(brng)) lon2: =lon1 + ATAN2(COS(d/R)-SIN(lat1)*SIN(lat2), SIN(brng)*SIN(d/R)*COS(lat1)) * Remember that Excel reverses the arguments to ATAN2 – see notes below |
For final bearing, simply take the initial bearing from the end point to the start point and reverse it (using θ = (θ+180) % 360).
Intersection of two paths given start points and bearings
This is a rather more complex calculation than most others on this page, but I've been asked for it a number of times. This comes from Ed William’s aviation formulary. See below for the JavaScript.
| Formula: | δ12 = 2⋅asin( √(sin²(Δφ/2) + cos φ1 ⋅ cos φ2 ⋅ sin²(Δλ/2)) ) if sin(λ2−λ1) > 0 α1 = (θ13 − θ12 + π) % 2π − π α3 = acos( −cos α1 ⋅ cos α2 + sin α1 ⋅ sin α2 ⋅ cos δ12 ) |
| where | φ1, λ1, θ1 : 1st point & bearing % = (floating point) modulo |
| note – | if sin α1 = 0 and sin α2 = 0: infinite solutions if sin α1 ⋅ sin α2 < 0: ambiguous solution this formulation is not always well-conditioned for meridional or equatorial lines |
This is a lot simpler using vectors rather than spherical trigonometry: see latlong-vectors.html.
Cross-track distance
Here’s a new one: I’ve sometimes been asked about distance of a point from a great-circle path (sometimes called cross track error).
| Formula: | dxt = asin( sin(δ13) ⋅ sin(θ13−θ12) ) ⋅ R |
| where | δ13 is (angular) distance from start point to third point θ13 is (initial) bearing from start point to third point θ12 is (initial) bearing from start point to end point R is the earth’s radius |
| JavaScript: | var dXt = Math.asin(Math.sin(d13/R)*Math.sin(θ13-θ12)) * R; |
Here, the great-circle path is identified by a start point and an end point – depending on what initial data you’re working from, you can use the formulæ above to obtain the relevant distance and bearings. The sign of dxt tells you which side of the path the third point is on.
The along-track distance, from the start point to the closest point on the path to the third point, is
| Formula: | dat = acos( cos(δ13) / cos(δxt) ) ⋅ R |
| where | δ13 is (angular) distance from start point to third point δxt is (angular) cross-track distance R is the earth’s radius |
| JavaScript: | var dAt = Math.acos(Math.cos(d13/R)/Math.cos(dXt/R)) * R; |
Closest point to the poles
And: ‘Clairaut’s formula’ will give you the maximum latitude of a great circle path, given a bearing θ and latitude φ on the great circle:
| Formula: | φmax = acos( | sin θ ⋅ cos φ | ) |
| JavaScript: | var φMax = Math.acos(Math.abs(Math.sin(θ)*Math.cos(φ))); |
Rhumb lines
A ‘rhumb line’ (or loxodrome) is a path of constant bearing, which crosses all meridians at the same angle.
Sailors used to (and sometimes still) navigate along rhumb lines since it is easier to follow a constant compass bearing than to be continually adjusting the bearing, as is needed to follow a great circle. Rhumb lines are straight lines on a Mercator Projection map (also helpful for navigation).
Rhumb lines are generally longer than great-circle (orthodrome) routes. For instance, London to New York is 4% longer along a rhumb line than along a great circle – important for aviation fuel, but not particularly to sailing vessels. New York to Beijing – close to the most extreme example possible (though not sailable!) – is 30% longer along a rhumb line.
Key to calculations of rhumb lines is the inverse Gudermannian function¹, which gives the height on a Mercator projection map of a given latitude: ln(tanφ + secφ) or ln( tan(π/4+φ/2) ). This of course tends to infinity at the poles (in keeping with the Mercator projection). For obsessives, there is even an ellipsoidal version, the ‘isometric latitude’: ψ = ln( tan(π/4+φ/2) / [ (1−e⋅sinφ) / (1+e⋅sinφ) ]e/2), or its better-conditioned equivalent ψ = atanh(sinφ) − e⋅atanh(e⋅sinφ).
The formulæ to derive Mercator projection easting and northing coordinates from spherical latitude and longitude are then¹
| E = R ⋅ λ | |
| N = R ⋅ ln( tan(π/4 + φ/2) ) |
The following formulæ are from Ed Williams’ aviation formulary.¹
Distance
Since a rhumb line is a straight line on a Mercator projection, the distance between two points along a rhumb line is the length of that line (by Pythagoras); but the distortion of the projection needs to be compensated for.
On a constant latitude course (travelling east-west), this compensation is simply cosφ; in the general case, it is Δφ/Δψwhere Δψ = ln( tan(π/4 + φ2/2) / tan(π/4 + φ1/2) ) (the ‘projected’ latitude difference)
| Formula: | Δψ = ln( tan(π/4 + φ2/2) / tan(π/4 + φ1/2) ) | (‘projected’ latitude difference) |
| q = Δφ/Δψ (or cosφ for E-W line) | ||
| d = √(Δφ² + q²⋅Δλ²) ⋅ R | (Pythagoras) | |
| where | φ is latitude, λ is longitude, Δλ is taking shortest route (<180°), R is the earth’s radius, ln is natural log | |
| JavaScript:
(all angles
in radians) |
var Δψ = Math.log(Math.tan(Math.PI/4+φ2/2)/Math.tan(Math.PI/4+φ1/2)); var q = Math.abs(Δψ) > 10e-12 ? Δφ/Δψ : Math.cos(φ1); // E-W course becomes ill-conditioned with 0/0 // if dLon over 180° take shorter rhumb across anti-meridian: if (Math.abs(Δλ) > Math.PI) Δλ = Δλ>0 ? -(2*Math.PI-Δλ) : (2*Math.PI+Δλ); var dist = Math.sqrt(Δφ*Δφ + q*q*Δλ*Δλ) * R; |
|
Bearing
A rhumb line is a straight line on a Mercator projection, with an angle on the projection equal to the compass bearing.
| Formula: | Δψ = ln( tan(π/4 + φ2/2) / tan(π/4 + φ1/2) ) | (‘projected’ latitude difference) |
| θ = atan2(Δλ, Δψ) | ||
| where | φ is latitude, λ is longitude, Δλ is taking shortest route (<180°), R is the earth’s radius, ln is natural log | |
| JavaScript:
(all angles
in radians) |
var Δψ = Math.log(Math.tan(Math.PI/4+φ2/2)/Math.tan(Math.PI/4+φ1/2));
var q = Math.abs(Δψ) > 10e-12 ? Δφ/Δψ : Math.cos(φ1); // E-W course becomes ill-conditioned with 0/0
// if dLon over 180° take shorter rhumb across anti-meridian:
if (Math.abs(Δλ) > Math.PI) Δλ = Δλ>0 ? -(2*Math.PI-Δλ) : (2*Math.PI+Δλ);
var brng = Math.atan2(Δλ, Δψ).toDegrees(); |
|
Destination
Given a start point and a distance d along constant bearing θ, this will calculate the destination point. If you maintain a constant bearing along a rhumb line, you will gradually spiral in towards one of the poles.
| Formula: | δ = d/R | (angular distance) |
| Δψ = ln( tan(π/4 + φ2/2) / tan(π/4 + φ1/2) ) | (‘projected’ latitude difference) | |
| q = Δφ/Δψ (or cosφ for E-W line) | ||
| Δλ = δ ⋅ sin θ / q | ||
| φ2 = φ1 + δ ⋅ cos θ | ||
| λ2 = λ1 + Δλ | ||
| where | φ is latitude, λ is longitude, Δλ is taking shortest route (<180°), ln is natural log, R is the earth’s radius | |
| JavaScript:
(all angles
in radians) |
var Δφ = δ*Math.cos(θ); var φ2 = φ1 + Δλ; var Δψ = Math.log(Math.tan(φ2/2+Math.PI/4)/Math.tan(φ1/2+Math.PI/4)); var q = Δψ > 10e-12 ? Δφ / Δψ : Math.cos(φ1); // E-W course becomes ill-conditioned with 0/0 var Δλ = δ*Math.sin(θ)/q; // check for some daft bugger going past the pole, normalise latitude if so if (Math.abs(φ2) > Math.PI/2) φ2 = φ2>0 ? Math.PI-φ2 : -Math.PI-φ2; λ2 = (λ1+dLon+Math.PI)%(2*Math.PI) - Math.PI; |
|
Mid-point
This formula for calculating the ‘loxodromic midpoint’, the point half-way along a rhumb line between two points, is due to Robert Hill and Clive Tooth1 (thx Axel!).
| Formula: | φm = (φ1+φ2) / 2 |
| f1 = tan(π/4 + φ1/2) | |
| f2 = tan(π/4 + φ2/2) | |
| fm = tan(π/4+φm/2) | |
| λm = [ (λ2−λ1) ⋅ ln(fm) + λ1 ⋅ ln(f2) − λ2 ⋅ ln(f1) ] / ln(f2/f1) | |
| where | φ is latitude, λ is longitude, ln is natural log |
| JavaScript:
(all angles
in radians) |
if (Math.abs(λ2-λ1) > Math.PI) λ1 += 2*Math.PI; // crossing anti-meridian
var φ3 = (φ1+φ2)/2;
var f1 = Math.tan(Math.PI/4 + φ1/2);
var f2 = Math.tan(Math.PI/4 + φ2/2);
var f3 = Math.tan(Math.PI/4 + φ3/2);
var λ3 = ( (λ2-λ1)*Math.log(f3) + λ1*Math.log(f2) - λ2*Math.log(f1) ) / Math.log(f2/f1);
if (!isFinite(λ3)) λ3 = (λ1+λ2)/2; // parallel of latitude
λ3 = (λ3+3*Math.PI) % (2*Math.PI) - Math.PI; // normalise to -180..+180°
|
Using the scripts in web pages
Using these scripts in web pages would be something like the following:
<script src="latlon.js">/* Latitude/Longitude formulae */</script>
<script src="geo.js">/* Geodesy representation conversions */</script>
...
<form>
Lat1: <input type="text" name="lat1" id="lat1"> Lon1: <input type="text" name="lon1" id="lon1">
Lat2: <input type="text" name="lat2" id="lat2"> Lon2: <input type="text" name="lon2" id="lon2">
<button onClick="var p1 = LatLon(Geo.parseDMS(f.lat1.value), Geo.parseDMS(f.lon1.value));
var p2 = LatLon(Geo.parseDMS(f.lat2.value), Geo.parseDMS(f.lon2.value));
alert(p1.distanceTo(p2));">Calculate distance</button>
</form>
If you use jQuery, the code can be separated from the HTML:
<script src="//ajax.googleapis.com/ajax/libs/jquery/1.11.1/jquery.min.js"></script>
<script src="latlon.js">/* Latitude/Longitude formulae */</script>
<script src="geo.js">/* Geodesy representation conversions */</script>
<script>
$(document).ready(function() {
$('#calc-dist').click(function() {
var p1 = LatLon(Geo.parseDMS($('#lat1').val()), Geo.parseDMS($('#lon1').val()));
var p2 = LatLon(Geo.parseDMS($('#lat2').val()), Geo.parseDMS($('#lon2').val()));
$('#result-distance').html(p1.distanceTo(p2));
});
});
</script>
...
<form>
Lat1: <input type="text" name="lat1" id="lat1"> Lon1: <input type="text" name="lon1" id="lon1">
Lat2: <input type="text" name="lat2" id="lat2"> Lon2: <input type="text" name="lon2" id="lon2">
<button id="calc-dist">Calculate distance</button>
<output id="result-distance"></output> km
</form>
Convert between degrees-minutes-seconds & decimal degrees
| Latitude | Longitude | ||
| 1° ≈ 111 km (110.57 eq’l — 111.70 polar) | |||
| 1′ ≈ 1.85 km (= 1 nm) | 0.01° ≈ 1.11 km | ||
| 1″ ≈ 30.9 m | 0.0001° ≈ 11.1 m | ||
Notes:
- Accuracy: since the earth is not quite a sphere, there are small errors in using spherical geometry; the earth is actually roughly ellipsoidal (or more precisely, oblate spheroidal) with a radius varying between about 6,378km (equatorial) and 6,357km (polar), and local radius of curvature varying from 6,336km (equatorial meridian) to 6,399km (polar). 6,371 km is the generally accepted value for the earth’s mean radius. This means that errors from assuming spherical geometry might be up to 0.55% crossing the equator, though generally below 0.3%, depending on latitude and direction of travel. An accuracy of better than 3m in 1km is mostly good enough for me, but if you want greater accuracy, you could use the Vincenty formula for calculating geodesic distances on ellipsoids, which gives results accurate to within 1mm. (Out of sheer perversity – I’ve never needed such accuracy – I looked up this formula and discovered the JavaScript implementation was simpler than I expected).
- Trig functions take arguments in radians, so latitude, longitude, and bearings in degrees (either decimal or degrees/minutes/seconds) need to be converted to radians, rad = π.deg/180. When converting radians back to degrees (deg = 180.rad/π), West is negative if using signed decimal degrees. For bearings, values in the range -π to +π [-180° to +180°] need to be converted to 0 to +2π [0°–360°]; this can be done by (brng+2.π)%2.π [or brng+360)%360] where % is the (floating point) modulo operator.
- The atan2() function widely used here takes two arguments, atan2(y, x), and computes the arc tangent of the ratio y/x. It is more flexible than atan(y/x), since it handles x=0, and it also returns values in all 4 quadrants -π to +π (the atan function returns values in the range -π/2 to +π/2).
- All bearings are with respect to true north, 0°=N, 90°=E, etc; if you are working from a compass, magnetic north varies from true north in a complex way around the earth, and the difference has to be compensated for by variances indicated on local maps.
- If you implement any formula involving atan2 in Microsoft Excel, you will need to reverse the arguments, as Excelhas them the opposite way around from
相關推薦
Calculate distance, bearing and more between Latitude/Longitude points
原文地址:http://www.movable-type.co.uk/scripts/latlong.html Movable Type Scripts Calculate distance, bearing and more between Latitude/Lon
計算兩個latitude-longitude點之間的距離? (Haversine公式)
org 程序 沒有 this rgs 完整 替換 5.5 self 問題描述 如何計算緯度和經度指定的兩點之間的距離?為了澄清,我想要距離公裏;這些點使用WGS84系統,我想了解可用方法的相對準確性。最佳解決方案 這個link可能對您有幫助,因為它詳細說明了使用Have
BiliBili, ACFun… And More!【遞歸算法】
double font include main color nbsp image stc class 題源:http://acm.uestc.edu.cn/#/problem/show/3 題解: 題意:播放一段視頻文件,有播放速度和緩沖速度兩種,因為作者的癖好
What is Web Application Architecture? How It Works, Trends, Best Practices and More
som put type ruby async sin porting whole ldb At Stackify, we understand the amount of effort that goes into creating great applications.
Macbook pro Version 14.0 cannot copy and paste between different applicatons after updated system
click one ebs book bubuko folder cbo AR ann Refer to : https://discussions.apple.com/thread/7679531 To fix a stuck clipboard (pasteboa
Best deals for Oct. 1: Save on Instant Pot, Epson printers, Beats headphones, Echo Show, LEGO, and more
October is here and so are some great sales. We've gathered the best deals on the products you want, including printers, headphones, kitchen gear, video st
Pots, Amazon Echo Show, LEGO sets, Samsung and LG 4K TVs, and more | AITopics
SEE ALSO: Neato vs. Roomba: Which robot vacuum best suits your cleaning needs? There are a number of high end 4K TVs on sale today, such as LG Electronics'
Best deals for Oct. 5: Save on Beats headphones, CBD oil, Cuisinart coffee makers, Amazon Echo Sub, and more
With the weekend finally here, we've gathered together the best deals to make your time away from work so much more enjoyable and relaxing. Speaking of rel
Made by Google Event 2018: What we expect and don't expect for Pixel, Google Home and more
While it might seem like the annual Made by Google event has already taken place based on the Pixel leaks we've received on a daily basis, we actually stil
GoLand 2018.3 EAP 2: dependency diagrams, High Contrast theme, better code completion for databases, and more
GoLand 2018.3 EAP 2 is available for download. By the way, you don’t have to wait for the official EAP announcements to try new features. Afte
B, iPads, CBD oil, KitchenAid mixers, Amazon Echo Show, and more | AITopics
The weekend is finally here, so we've rounded up the best deals on dental hygiene products and kitchen gear and more. We also have deals on adult learning
Video Friday: Boston Dynamics' Spot Goes to Work, and More
Video Friday is your weekly selection of awesome robotics videos, collected by your Automaton bloggers. We'll also be posting a weekly calendar of upcoming
EVGA GeForce RTX 2070 XC review: Cheaper and more feature
EVGA's custom GeForce RTX 2070 XC graphics card is cooler, more customizable, and just as fast as Nvidia's RTX 2070 Founders Edition. It's packing dedicate
Best deals for Oct. 16: Xbox One S, Nintendo Switch games, Amazon Fire TV Stick 4K, and more on sale
If you have ever felt the shoulder ache brought on by too much gaming, have an indent permanently worn into your couch in your "spot," or have ever blown o
Show HN: Tools for tracking cigarette litter in SF (and more)
Hi all,We're working on tools to map and clean litter. We have an iOS app and a fancy "picker-upper" you can see in this video: https://www.youtube.com/wat
Deals to die for: Save on Samsung 4K TVs, Lenovo laptops, Roombas, and more during the Night of the Living Deals sales event
Editor's note: Mashable and IGN are both owned by Ziff Davis. If you're super jazzed about the spooky season (raises hand), we're guessing you've been stra
Best deals for Oct. 17: Save on Apple iPad Pro, LG 4K TVs, Dyson vacuums, Audible, Echo Show, and more
Save on tablets, vacuums, and Amazon devices, plus get fantastic discounts from IGN's 24-hour deals event Night of the Living Deals, which goes through Oct
CLI Prompts, Virtual Scroll, Drag and Drop and more
Version 7 of Angular — CLI Prompts, Virtual Scroll, Drag and Drop and moreThe 7.0.0 release of Angular is here! This is a major release spanning the entire
The “exposome” revealed: a barrage of bacteria, chemicals, microscopic animals and more
The “exposome” revealed: a barrage of bacteria, chemicals, microscopic animals and moreScientists have measured the human “exposome,” or the particulates,
build SDK Indices, Debugger Improvements, and More | GoLand Blog
A couple of weeks ago we started the EAP for GoLand 2018.2, our next major update. In the first EAP build, we’ve added initial support for vgo
