暴力遞迴轉動態規劃-----2
例題一:
換錢的方法數
給定陣列arr,arr中所有的值都為正數且不重複。每個值代表一種面值的貨幣,每種面值的貨幣可以使用任意張,再給定一個整數aim代表要找的錢數,求換錢有多少種方法。
【舉例】
arr=[5,10,25,1],aim=0。
組成0元的方法有1種,就是所有面值的貨幣都不用。所以返回1。
arr=[5,10,25,1],aim=15。
組成15元的方法有6種,分別為3張5元、1張10元+1張5元、1張10元+5張1元、10張1元+1張5元、2張5元+5張1元和15張1元。所以返回6。
arr=[3,5],aim=2。
任何方法都無法組成2元。所以返回0。
思路:
最暴力的解法:
我們定義一個遞迴函式GetNumber(Aim,index),代表只能從arr陣列index位置及以後的位置換錢,能夠正好組成面值為Aim的方法數。
程式碼:
#include<algorithm> #include<iostream> #include<limits.h> #include <sstream> #include<cstdlib> #include<cstring> #include<cassert> #include<string> #include<cstdio> #include<bitset> #include<vector> #include<cmath> #include<ctime> #include<stack> #include<queue> #include<deque> #include<list> #include<set> #define mod 1000000007 #define MAXN 1000001 typedef long long ll; using namespace std; int arr[MAXN]; int n,aim; int GetNumber(int Aim,int index) { if(index==n) //到達了arr陣列的最後的位置 return Aim==0?1:0;//如果Aim為0,說明找到了一種換錢的方法,返回1 int ans=0; for(int i=0;i*arr[index]<=Aim;i++)//列舉arr陣列當前位置所代表的錢的張數 ans+=GetNumber(Aim-i*arr[index],index+1); return ans; } int main() { cin>>n>>aim; for(int i=0;i<n;i++) cin>>arr[i]; cout<<GetNumber(aim,0)<<endl; }
我們來分析一下這種方法為何暴力:
我們以題目中第二組例子為例
arr=[5,10,25,1],aim=15
對於這組例子,程式肯定會進入GetNumber(3,15)這個函式(前面選擇了兩張5元的,0張10元的或者選擇了0張5元的,一張10元的),所以,對於GetNumber(3,15)這一個遞迴函式,前面的兩個狀態都能夠到達,這就出現了重複計算,使得演算法時間複雜度變得很高。
第一版優化-----記憶化搜尋:
通過上面的分析,我們可以將算出的結果存在一個數組中,後續程式的計算如果需要某個結果直接從陣列中拿就可以了,例如我們可以將GetNumber(3,15)這個函式算出的結果存在一個數組中,如果後面的計算還需要GetNumber(3,15)這個函式算出的結果的話,就可以直接從陣列中拿出來了,避免的重複計算。
程式碼:
#include<algorithm>
#include<iostream>
#include<limits.h>
#include <sstream>
#include<cstdlib>
#include<cstring>
#include<cassert>
#include<string>
#include<cstdio>
#include<bitset>
#include<vector>
#include<cmath>
#include<ctime>
#include<stack>
#include<queue>
#include<deque>
#include<list>
#include<set>
#define mod 1000000007
#define MAXN 10001
typedef long long ll;
using namespace std;
int visited[MAXN][MAXN];//將計算結果存在這個陣列中,橫座標代表arr陣列的下標索引,縱座標代表Aim的變化
int arr[MAXN];
int n,aim;
int GetNumber(int Aim,int index)
{
if(visited[index][Aim]!=-1)//陣列中存在GetNumber(Aim,index)這個函式的返回值,直接從陣列中拿就行了
return visited[index][Aim];
if(index==n)
return Aim==0?1:0;
int ans=0;
for(int i=0;i*arr[index]<=Aim;i++)
ans+=GetNumber(Aim-i*arr[index],index+1);
visited[index][Aim]=ans;//給visited陣列賦值
return ans;
}
int main()
{
cin>>n>>aim;
for(int i=0;i<n;i++)
cin>>arr[i];
memset(visited,-1,sizeof(visited));
cout<<GetNumber(aim,0)<<endl;
}
第二版優化---動態規劃版本:
我們可以根據暴力解法直接寫出動態規劃的版本,具體如何寫這裡就不講了,我的另一個部落格已經寫了,可以去看那一個部落格。
這裡我們講一下改完動態規劃後還有一個優化,

通過分析我們可以得到這樣一張圖,圖中五角星位置就是我們要求的位置,四角星位置是任意一個位置,那麼通過分析可以得到,四角星位置是由它的下一行的三個心型位置的值累加得到的,而六角星位置是由它的下一行前兩個心型位置的值累加得到的,所以,通過觀察可以得到四角星位置可以由同行的六角星位置加上它正下方的心型位置上的值累加的到,這就是一個優化。
可以使得在寫程式碼時兩重迴圈裡面不用在套一個while迴圈。
程式碼:
#include<algorithm>
#include<iostream>
#include<limits.h>
#include <sstream>
#include<cstdlib>
#include<cstring>
#include<cassert>
#include<string>
#include<cstdio>
#include<bitset>
#include<vector>
#include<cmath>
#include<ctime>
#include<stack>
#include<queue>
#include<deque>
#include<list>
#include<set>
#define mod 1000000007
#define MAXN 10001
typedef long long ll;
using namespace std;
int visited[MAXN][MAXN];
int arr[MAXN];
int n,aim;
int main()
{
cin>>n>>aim;
for(int i=0;i<n;i++)
cin>>arr[i];
memset(visited,0,sizeof(visited));
visited[n][0]=1;
for(int i=n-1;i>=0;i--)
for(int j=0;j<=aim;j++)
if(j-arr[i]>=0)
visited[i][j]=visited[i][j-arr[i]]+visited[i+1][j];//這就是我們所分析出來的狀態轉移方程
else
visited[i][j]=visited[i+1][j];//如果越界了,就只加下面那個就好
cout<<visited[0][aim]<<endl;
}例題二:
排成一條線的紙牌博弈問題
【題目】
給定一個整型陣列arr,代表數值不同的紙牌排成一條線。玩家A和玩家B依次拿走每張紙牌,規定玩家A先拿,玩家B後拿,但每個玩家每次只能拿走最左或最右的紙牌,玩家A和玩家B都絕頂聰明。請返回最後獲勝者的分數。
【舉例】
arr=[1,2,100,4]。開始時玩家A只能拿走1或4。如果玩家A拿走1,則排列變為[2,100,4],接下來玩家B可以拿走2或4,然後繼續輪到玩家A。如果開始時玩家A拿走4,則排列變為[1,2,100],接下來玩家B可以拿走1或100,然後繼續輪到玩家A。玩家A作為絕頂
聰明的人不會先拿4,因為拿4之後,玩家B將拿走100。所以玩家A會先拿1,讓排列變為[2,100,4],接下來玩家B不管怎麼選,100都會被玩家A拿走。玩家A會獲勝,分數為101。所以返回101。
arr=[1,100,2]。
開始時玩家A不管拿1還是2,玩家B作為絕頂聰明的人,都會把100拿走。玩家B會獲勝,分數為100。所以返回100。
思路:
暴力求解思路:
這篇部落格暴力求解的思路寫的不錯:
https://blog.csdn.net/zxzxzx0119/article/details/81274473
通過這篇部落格所寫的思路,我們就可以寫出遞迴函式。
程式碼:
#include<algorithm>
#include<iostream>
#include<limits.h>
#include <sstream>
#include<cstdlib>
#include<cstring>
#include<cassert>
#include<string>
#include<cstdio>
#include<bitset>
#include<vector>
#include<cmath>
#include<ctime>
#include<stack>
#include<queue>
#include<deque>
#include<list>
#include<set>
#define mod 1000000007
#define MAXN 100001
typedef long long ll;
using namespace std;
int n;
int arr[MAXN];
int End(int i,int j);
int Frist(int i,int j)//玩家作為先手在陣列i位置到j位置上選擇能夠得到的最大分數
{
if(i==j)//只有一張牌了,先手拿走
return arr[i];
return max(End(i+1,j)+arr[i],End(i,j-1)+arr[j]);//如果該玩家作為先手在i位置到j位置拿牌,那麼該玩家在(i+1位置到j位置)或者在(i位置到j-1位置)上就作為了後手
}
int End(int i,int j)//玩家作為後手在陣列i位置到j位置上選擇能夠得到的最大分數
{
if(i==j)//只有一張牌了,後手沒有機會拿了,先手拿走,所以返回零
return 0;
return min(Frist(i+1,j),Frist(i,j-1));//這個地方不太明白啥意思
}
int main()
{
cin>>n;
for(int i=0;i<n;i++)
cin>>arr[i];
cout<<max(Frist(0,n-1),End(0,n-1))<<endl;
}暴力遞迴轉動態規劃思路:
還是原先的那幾個步驟,只不過這裡有兩個遞迴函式,所以我們要建立兩個dp表,讓這兩個表相互推數,最終得到我們想要的結果。
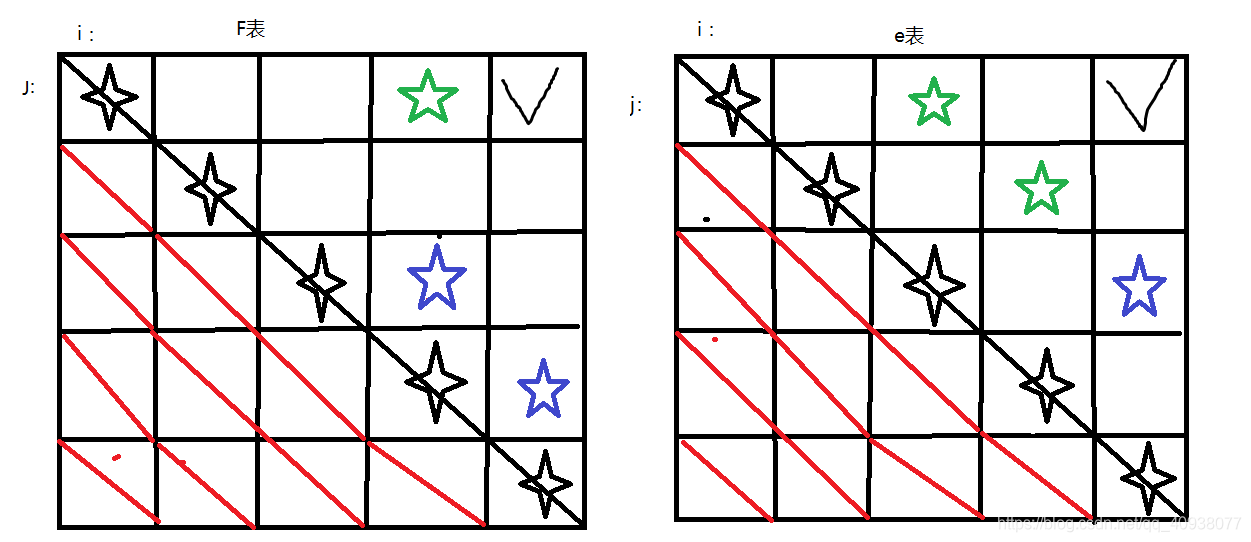
觀察上圖,F表代表上述程式碼中的Frist函式,e表代表上述程式碼中的End函式,通過觀察遞迴函式可以得到,表中的√位置就是我們要求的位置,表中的四角星位置就是我們的初始值位置,不需要計算就可以得到,F表中綠色五角星位置上的數的計算需要用到e表中的兩個綠色五角星位置上的數,e表中的藍色五角星位置上的數的計算需要用到F表中的兩個藍色五角星位置上的數。
需要注意迴圈的順序。
程式碼:
#include<algorithm>
#include<iostream>
#include<limits.h>
#include <sstream>
#include<cstdlib>
#include<cstring>
#include<cassert>
#include<string>
#include<cstdio>
#include<bitset>
#include<vector>
#include<cmath>
#include<ctime>
#include<stack>
#include<queue>
#include<deque>
#include<list>
#include<set>
#define mod 1000000007
#define MAXN 1001
typedef long long ll;
using namespace std;
int n;
int arr[MAXN];
int f[MAXN][MAXN],e[MAXN][MAXN];
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
cin>>arr[i];
memset(f,0,sizeof(f));
memset(e,0,sizeof(e));
for(int i=1;i<=n;i++)//給兩個表賦初值
{
f[i][i]=arr[i];
e[i][i]=0;
}
for(int i=n-1;i>=1;i--)//注意迴圈的順序
for(int j=i+1;j<=n;j++)
{
f[i][j]=max(e[i+1][j]+arr[i],e[i][j-1]+arr[j]);//狀態轉移方程
e[i][j]=min(f[i+1][j],f[i][j-1]);
}
cout<<max(f[1][n],e[1][n])<<endl;
}例題三:
題目:
初始給你N個位置,1位置到N位置,然後有一個機器人,初始停留在M位置上,然後告訴你這個機器人可以走P步,如果機器人初始位置在1位置,那麼他只能往右走,如果機器人初始位置在N位置,那麼他只能往左走,否則,這個機器人即能往左走,也能往右走,問你,這個機器人走P步之後停在K位置的走的方法數有多少種。
思路:
暴力遞迴的思路:
我們定義遞迴函式process(m,p)代表機器人走到m位置,還剩p步可以走的能夠到達K位置的走法數。這樣我們就可以寫出遞迴函數了。
程式碼:
#include<algorithm>
#include<iostream>
#include<limits.h>
#include <sstream>
#include<cstdlib>
#include<cstring>
#include<cassert>
#include<string>
#include<cstdio>
#include<bitset>
#include<vector>
#include<cmath>
#include<ctime>
#include<stack>
#include<queue>
#include<deque>
#include<list>
#include<set>
#define mod 1000000007
typedef long long ll;
using namespace std;
int N,M,P,K;
// N 格子數
// M 初始的位置
// P 要走的步數
// K 最後要停留的位置
int process(int m,int p)//m代表當前走到的位置,p代表還剩餘多少步可以走
{
if(p==0) // 沒有步數可以走了,看一下現在的位置是否為K,如果是,返回1.如果不是,返回0
return m==K?1:0;
if (m==1) // 現在的位置在最左邊,只能往右走
return process(m+1,p-1);
else if(m==N) //現在的位置在最右邊,只能往左走
return process(m-1,p-1);
else
return process(m-1,p-1)+process(m+1,p-1); //普遍位置
}
int main()
{
while (1)
{
cin>>N>>M>>P>>K;
if(N<2||M<1||M>N||P<0||K<1||K>N)//這都是無效的輸入
{
cout<<0<<endl;
continue ;
}
cout<<process(M,P)<<endl;//呼叫遞迴函式
}
}動態規劃的思路:
這個遞迴函式改動態規劃很簡單,通過分析我們可以得到下面這個圖:
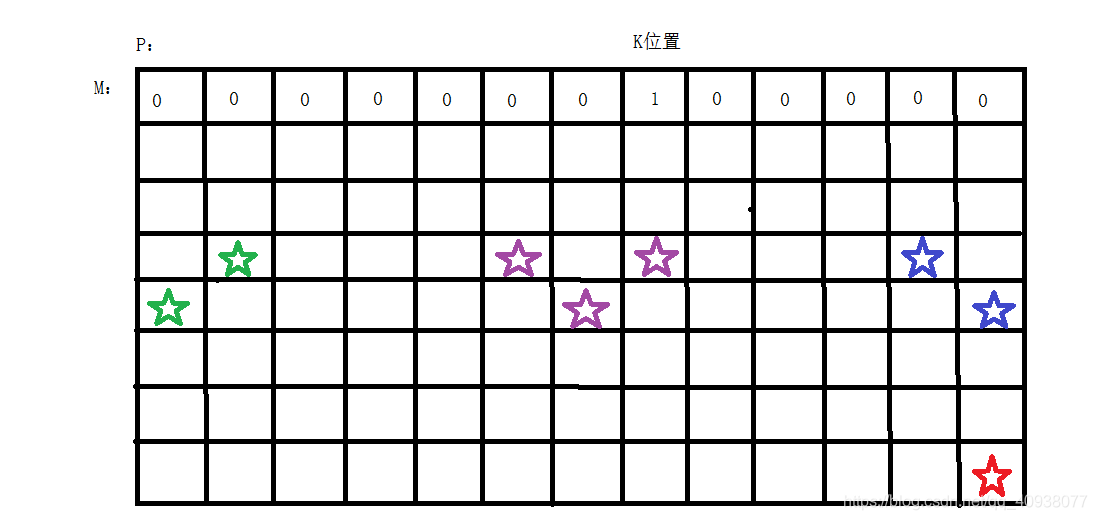
圖中:
紅色的五角星:我們需要求的位置
綠色的五角星:最左邊的位置,需要它右上的綠色五角星位置上的數
藍色的五角星:最右邊的位置,需要它左上的藍色五角星位置上的數
紫色的五角星:普遍的位置,需要它右上和左上的紫色五角星位置上的數字
程式碼:
#include<algorithm>
#include<iostream>
#include<limits.h>
#include <sstream>
#include<cstdlib>
#include<cstring>
#include<cassert>
#include<string>
#include<cstdio>
#include<bitset>
#include<vector>
#include<cmath>
#include<ctime>
#include<stack>
#include<queue>
#include<deque>
#include<list>
#include<set>
#define mod 1000000007
#define MAXN 10001
typedef long long ll;
using namespace std;
int N,M,P,K;
// N 位置的個數
// M 初始的位置
// P 要走的步數
// K 最後要停留的位置
int dp[MAXN][MAXN];//dp表
int main()
{
cin>>N>>M>>P>>K;
memset(dp,0,sizeof(dp));
dp[0][K]=1;
for(int i=1;i<=P;i++)
{
for(int j=1;j<=N;j++)
{
if(j==1)//最左邊的位置
dp[i][j]=dp[i-1][j+1];
else if(j==N)//最右邊的位置
dp[i][j]=dp[i-1][j-1];
else // 普遍位置
dp[i][j]=dp[i-1][j-1]+dp[i-1][j+1];
}
}
cout<<dp[P][M]<<endl;
}
