第一講行與列的思考
1.從問題出發，如果現有一組二元一次方程：
2x-y=0
-x+2y=3
寫成矩陣的形式就是
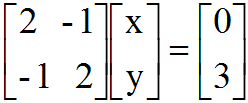，即Ax=b
他得行影象遵從幾何描述，即兩條直線的交點。
他的列影象則是兩個向量的線性代數組合。
當矩陣右邊b變化的時候，行向量描述的幾何圖形會隨之改變，而列向量描述的兩個底向量卻不會變，只是他們的線性組合變了。
2.方程組的解
對於行影象來說，解即為交點，如果兩直線平行顯然是沒有交點的，此時矩陣的行列式值=0，且不可逆（無法還原成單位矩陣），是奇異矩陣。
對於列影象來說，解即為向量線性組合的係數。只有當b代表的向量與所有底向量都垂直時候無解。對應的可能向量組是線性相關。
相關推薦
第一講行與列的思考
1.從問題出發，如果現有一組二元一次方程： 2x-y=0 -x+2y=3 寫成矩陣的形式就是 ，即Ax=b 他得行影象遵從幾何描述，即兩條直線的交點。 他的列影象則是兩個向量的線性代數組合。 當矩陣右邊b變化的時候，行向量描述的幾何圖
DataGridView獲取當前選中的行與列的值
版權宣告：本文為博主原創文章，引用如需標註必須出處 https://blog.csdn.net/qq_37227093/article/details/84335798 &nbs
python中pandas.DataFrame對行與列求和及新增新行與列示例
本文介紹的是python中pandas.DataFrame對行與列求和及新增新行與列的相關資料，下面話不多說，來看看詳細的介紹吧。 方法如下： 匯入模組： ? 1 2 3 from pandas import DataFrame import panda
程式設計師面試金典1.7：若M*N矩陣中某個元素為0，則將其所在的行與列清零
1.7：編寫一個演算法，若M*N矩陣中某個元素為0，則將其所在的行與列清零。 咋一看，這個問題很簡單：直接遍歷整個矩陣，只要發現值為0的元素，就將其所在的行與列清零。不過這種方法有個缺陷：在讀取被清零的行與列時，讀到的盡是零，於是所在的行與所在的列都變成了0，很快，整個矩陣
ALV例項：預設選擇行與列
DATA : lt_column TYPE salv_t_column, lr_selections TYPE REF TO cl_salv_selections, lt_row TYPE salv_t_
【Java】若MxN矩陣中某個元素為0， 則將其所在的行與列清零
若直接遍歷整個矩陣，發現為零的元素就直接將所在行與列清零，這樣做有一個陷阱，在讀取已被清零的行或列時，讀到的全是零，於是所在的行或列都變成零。 很快整個矩陣的所有元素都全部變為零了。 其實我們並不關心具體的行號和列號，反正整行和整列都會被清零，我們可以標記出零元素的行號和列
若M*N階矩陣中某個元素為0，則將其所在的行與列清零
#include <bits/stdc++.h> using namespace std; struct Matrix { int data; int flag; }; int main() { struct Matrix a[10][10
WPF－使用程式碼建立Grid行與列，並將控制元件新增到Grid中的指定行指定列
在c#中，有時需要通過程式碼建立面板控制元件，但是對於面板的操作與之前的控制元件並不是很直觀，因此記下方法，以供後來複習使用： 建立兩行兩列的表格： 第一種方法： Grid grid = new Grid(); RowDefinition row1 = new RowDefiniti
T-SQL行合並成列與列拆分成行
ont blank target where 感覺 一點 code returns bbb 原文:T-SQL行合並成列與列拆分成行 本文出處：http://www.cnblogs.com/wy123/p/6910468.html 感覺最近sql也沒少
sql的行轉列(PIVOT)與列轉行(UNPIVOT)
列轉行 gif 而且 碼農 實現 score username info rect 在做數據統計的時候，行轉列，列轉行是經常碰到的問題。case when方式太麻煩了，而且可擴展性不強，可以使用 PIVOT，UNPIVOT比較快速實現行轉列，列轉行，而且可擴展性強
MySQL行轉列與列轉行
展示 course order by rem core null innodb tail mysql 行轉列 例如：把圖1轉換成圖2結果展示 圖1 圖2 CREATE TABLE `TEST_TB_GRADE` ( `ID` int(10) NOT NU
[Js高手之路第一部]JavaScript上百例實戰【新版】_9 javascript二重循環乘法表與n行n列的表格
write wid AR meta else HA char 變色 col 0.隔行變色的表格 HTML style 屬性實現 1 <!DOCTYPE html> 2 <html lang="en"> 3 <head>
Docker系列:第一講.Docker簡介與安裝
安裝 -- docker-ce 資源 terminal 輸入 英文 docke 技術支持 什麽是 Docker？ Docker的英文翻譯是“搬運工”的意思，他搬運的東西就是我們常說的集裝箱Container，Container 裏面裝的是任意類型的 App，我們的開發人員可
行儲存與列儲存
1 為什麼要按列儲存 列式儲存(Columnar or column-based)是相對於傳統關係型資料庫的行式儲存(Row-basedstorage)來說的。簡單來說兩者的區別就是如何組織表(翻譯不好，直接抄原文了)： Ø Row-based storage stores
行式資料庫與列式資料庫的對比
導語：隨著大資料的發展，現在出現的列式儲存和列式資料庫。它與傳統的行式資料庫有很大區別的。 正文： 行式資料庫是按照行儲存的，行式資料庫擅長隨機讀操作不適合用於大資料。像SQL server,Oracle，mysql等傳統的是屬於行式資料庫範疇。 列式資料庫從一開始就是面向大資料環境下資
Pandas讀檔案(不把第一行作列屬性)
import pandas as pd #read_table可以指定分隔符 data1 = pd.read_csv("test.csv")#自動把第一行作列屬性，第一行不能用 data2 = pd.read_csv("test.cvs",header=None)#不把第一行作列屬性 da
DataFrame如何對某行某列的單個元素進行替換(.loc[]與.iloc[]區別)
DataFrame如何對某行某列的單個元素進行替換(.loc[]與.iloc[]區別) 在DataFrame檔案中，對i行j列的那個元素進行替換、插入資料操作，採用的是pd.loc[] pd.iloc[i,j] i,j 只能是數字，即原始索引。 pd.loc[i
《深度學習網路訓練--第一講》資料採集與資料預處理
經過專案的實踐，我感受到要想訓練出一個性能優良的模型網路，資料採集與預處理是多麼的艱難與重要。 資料的採集 資料的採集是一個費時費力的過程。對於人臉資料來說，針對產品的應用場景，需要採集不同環境變數的人臉影象。對於我的經驗來說，公司想要做一個人臉識別的A
Pandas入門基礎（二）：DataFrame的行、列與資料型別
建立DataFrame資料： data = {'state': ['Ohio', 'Ohio', 'Ohio', 'Nevada', 'Nevada', 'Nevada'], 'year': [2000, 2001, 2002, 2001, 20
關於python的pandas獲取csv\Excel的第一行（列標籤）
在Python中，經常會去讀csv檔案，如下 import pandas as pd import numpy as np df = pd.read_csv("url.csv") data = np.array(df.loc[:,:]) 通過這種方式得到的da