求最長迴文子串的演算法比較經典的是manacher演算法

轉載自這裡

首先，說明一下用到的陣列和其他引數的含義：

（1）p[i] ： 以字串中下標為的字元為中心的迴文子串半徑長度；

例如：abaa字串，那麼p[1]=2,（以b為中心的迴文子串是aba，半徑長度為2。計算半徑時包括b本身）
所以，陣列的最大值就是最長迴文串的半徑。

（2）id
id 為當前已確定的邊界能伸展到最靠右的迴文串的中心。

例如：

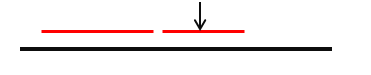
• 設黑色的線段表示字串範圍
• 紅色的線段表示當前已經確定的迴文子串在主串中的範圍

雖然左邊的紅色線段（左邊的迴文子串）長度比右邊長，但是，記錄的中心是右邊紅色線段的中心，因為右邊的迴文子串伸展更靠右。（下面將會解釋為什麼要記錄這個id值）

manacher演算法是從左到右掃描的，所以，在計算時，都是已知的。

manacher演算法

假設現在掃描到主串下標為的字元，那麼，以為中心的迴文子串最可能和之前已經確定的哪個迴文子串有交集？ 沒錯，就是能伸展最靠右的迴文子串，也就是以為中心的迴文子串。至於這個交集有什麼用，下面將解釋。

以i為中心的迴文串和以id為中心的迴文串如果有交集，會出現三種情況：

（1）

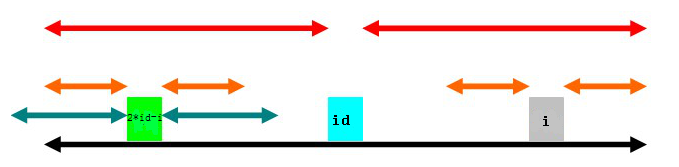
其中，2*id-i為i以id為中心的對稱位置。（2*id-i這個就不用多說了吧，計算一下就得到了）

第一種情況是（上圖），以2id-i為中心的迴文子串左端超出了以id為中心的迴文子串（綠色部分左端超出黑色部分左端）。那麼，根據迴文串的特點，知道以2

這種情況下, p[i]=p[id]+id-i (橙色部分的長度)

那麼，以i為中心的橙色部分有沒有可能更長？這是不可能的，假設還可以更長，如下：

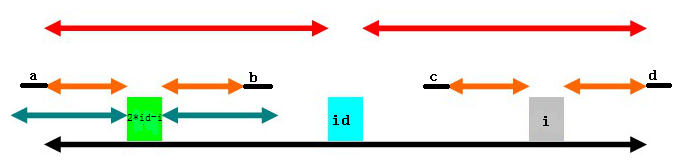
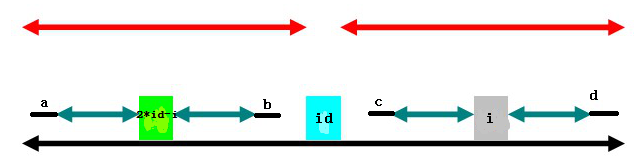
a和b對稱，b和c對稱，c和d對稱，最終得到a和d對稱，那麼，以id為中心的迴文串長度就不是下面黑色部分的長度了，而應左端加a右端加d，與已經求得的長度矛盾。

所以這種情況下: p[i]=p[id]+id-i

（2）

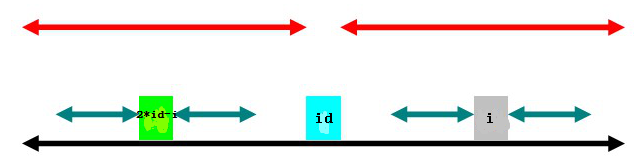
第二種情況是以2*id-i為中心的迴文子串在以id為中心的迴文子串內，如上圖。此時，p[i]=p[2*id-i]

同樣，c和d對稱，b和c對稱，a和d對稱，得到a和b對稱，那麼以2*id-i為中心的迴文子串長度就不是綠色部分的長度了，需要左端加a右端加b，與以求得的長度矛盾。

所以，這種情況下 p[i]=p[2*id-i]。

（3）

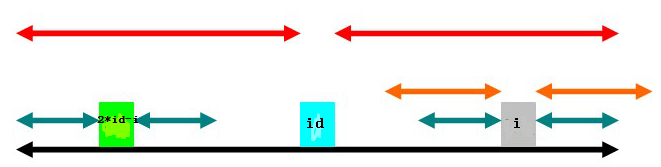
第三種情況是，以2*id-i為中心的迴文子串左端與以id為中心的迴文子串的左端恰好重合。則有。也就是說在的基礎上，還可能增加，即以i為中心的綠色部分還可能伸展。

所以，需要用一個while迴圈來確定它能增加多少。while迴圈為：

while (s[i - p[i]] == s[i + p[i]])
	++p[i];

也就是判斷綠色兩端（下圖淺黑色線段）是否相同，如果相同，就可以不斷增加。（理解p[i]的意思，就理解這個迴圈了）

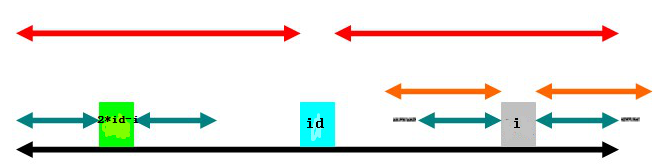
如果沒有出現交集(上面三種情況)，那麼就以i為中心點找最長迴文子串(下面程式碼中else的情況)。所以，演算法主要是利用迴文串的交集來減少計算。

如果我們將上面的情況總結起來，程式碼將非常簡潔：

if (p[id] + id - 1 >= i)
//沒有超出當前邊界最右的迴文串，也就是上面出現交集三種情況中的一種
     p[i] = Min(p[2 * id - i], p[id] + id - i);
else//如果沒有交集，就以它為中心求迴文串長度
  p[i] = 1;
 
while (s[i - p[i]] == s[i + p[i]])
   ++p[i];

最後，需要注意的是，上面的討論都是以某個字元為中心的迴文串，比如像這樣的迴文串：aabaa (長度為奇數)。但是，如果是這樣的迴文串：aabbaa(長度為偶數)，就沒法處理。

我們可以通過插入特殊符號（如‘#’）的辦法，將字串統一為奇數長度，如aabaa 變為 #a#a#b#a#a# ;同理，aabbaa變為#a#a#b#b#a#a#

注意到，上面的程式碼：

while (s[i - p[i]] == s[i + p[i]])
     ++p[i];

可能越界(超過頭或尾),我們可以通過頭尾也加入不相同的特殊符號處理，如aabaa 變為 $ #a#a#b#a#a# @。這種辦法為什麼可行呢？我們舉個例子，還是以aabaa為例，它變成 $ #a#a#b#a#a# @。當i指向第一個a時（也就是i=2），這時，s[i-1]==s[i+1]；繼續比較s[i-2]≠s[i+2]（也就是比較$和a），就不會超過頭。所以，就避免了越界的現象。末尾加個@也是同樣的道理。

最長迴文串的長度是maxlen-1
解釋

• p[i]為迴文串的半徑，如果該半徑是以 # 開始，即 # s[i] #....# 則一定以 # 結束，所以 maxlen-1 ,恰好是 s[] 和 # 一樣多，也就是maxlen-1是原串以 i 為中心的迴文串的長度
• 如果該半徑是以s[]開頭，即 ....# s[i-1] # s[i] # s[i+1] #.... ，顯然迴文串的長度是p[i]-1

下面是hihoCoder的一道求最長迴文子串的題：http://hihocoder.com/problemset/problem/1032

#include<iostream>  
#include<string>  
 
int Min(int a, int b)
{
	if (a < b)
		return a;
	return b;
}
 
int LPS(std::string &s)
{
	std::string new_s="";
	int s_len = s.length();
 
	new_s.resize(2 * s_len + 3);
 
	int new_s_len = new_s.length();
	
	new_s[0] = '$';
	new_s[1] = '#';
	new_s[new_s_len - 1] = '@';
 
	for (int i = 0,j=2; i < s_len; ++i)
	{
		new_s[j++] = s[i];
		new_s[j++] = '#';
	}
	
	int *p = new int[new_s_len + 1];
	int id = 0;//記錄已經查詢過的邊界最靠右迴文串的中心
	int maxLPS = 1;
	p[0] = 1;
	for (int i = 1; i < new_s_len-1; ++i)
	{
		if (p[id] + id - 1 >= i)//有交集的情況
			p[i] = Min(p[2 * id - i], p[id] + id - i);
		else//無交集的情況
			p[i] = 1;
 
		while (new_s[i - p[i]] == new_s[i + p[i]])
		//確定能伸展多少，上面if的情況是不會執行這個迴圈的
			++p[i];
 
		if (p[id] + id < p[i] + i)//重新確定伸展最右的迴文子串中心
			id = i;
		if (p[i]>maxLPS)//儲存當前最長迴文子串的長度(還要-1)
			maxLPS = p[i];
	}
	delete[] p;
	return maxLPS - 1;
}
 
int main()
{
	int N;
	std::string s;
	std::cin >> N;
	while (N--)
	{
		std::cin >> s;
		std::cout<<LPS(s)<<std::endl;
	}
	return 0;
}

HDU3068 使用C語言字元陣列來加快速度

#include<stdio.h>
#include<algorithm>
#include<string.h>
#include<iostream>
#include<math.h>
#include<queue>
#include<map>
#include<vector>
using namespace std;
#define inf 0x3f3f3f3f
#define ll long long
const int maxn=2e5+10;
char s[maxn],new_s[maxn*2];

int LPS(){
    int s_len=strlen(s);
    int new_s_len=s_len*2+3;

    new_s[0]='$';
    new_s[1]='#';
    new_s[new_s_len-1]='@';

    int i,j;
    for(i=0,j=2;i<s_len;i++){
        new_s[j++]=s[i];
        new_s[j++]='#';
    }
    new_s[j]='\0';

    int *p=new int[new_s_len+1];
    int id=0;
    int maxLPS=1;
    p[0]=1;
    for(int i=1;i<new_s_len;i++){
        if(p[id]+id-1>=i)
            p[i]=min(p[2*id-i],p[id]+id-i);
        else
            p[i]=1;
        while(new_s[i-p[i]]==new_s[i+p[i]])
            p[i]++;
        if(p[id]+id<p[i]+i)
            id=i;
        if(p[i]>maxLPS)
            maxLPS=p[i];
    }
    delete[] p;
    return maxLPS-1;
}
int main(){
    int ca=1;
    while(scanf("%s",s)!=EOF){
        memset(new_s,0,sizeof new_s);
        printf("%d\n",LPS());
    }
    return 0;
}

更加高效簡單的寫法

#include<stdio.h>
#include<algorithm>
#include<string.h>
#include<iostream>
#include<math.h>
#include<queue>
#include<map>
#include<vector>
using namespace std;
#define inf 0x3f3f3f3f
#define ll long long
const int maxn=2e5+10;
char s[maxn<<1];
int p[maxn<<1];//p[i]是迴文串的半徑

int LPS(){
    int len=strlen(s);
    int maxlen=1;//最長迴文字串的長度
    int id=0;
    for(int i=len;i>=0;i--){//插入len+1個”#“
        s[i+i+2]=s[i];
        s[i+i+1]='#';
    }
    //最終的S的長度是1~2*len+1

    s[0]='*';//防止while時p[i]越界
    for(int i=2;i<2*len+1;i++){
        if(p[id]+id>i)
            p[i]=min(p[2*id-i],p[id]+id-i);
        else
            p[i]=1;
        while(s[i-p[i]]==s[i+p[i]])
            p[i]++;
        if(id+p[id]<i+p[i])
            id=i;
        if(maxlen<p[i])
            maxlen=p[i];
    }
    return maxlen-1;
}
int main(){
    while(scanf("%s",s)!=EOF){
        printf("%d\n",LPS());
    }
    return 0;
}