運籌系列16:routing模型之VRP問題
阿新 • • 發佈:2018-11-24
1. 問題模型
VRP問題是車輛路徑問題的縮寫。問題是:有N輛車,都從原點出發,每輛車訪問一些點後回到原點,要求所有的點都要被訪問到,求最短的車輛行駛距離或最少需要的車輛數或最小化最長行駛距離。
常見的限制要求包括:車輛容量限制、時間窗限制、點訪問順序要求等。
2. RoutingModel的一些說明
對於VRP問題,我們可以使用ortools的RoutingModel模型。首先為車新增用於進行優化的dimension:
| 方法 | 輸入 | 說明 |
|---|---|---|
| AddDimension | evaluator, slack_max, capacity, fix_start_cumul_to_zero, name | Creates a dimension where the transit variable is constrained to be equal to evaluator(i, next(i)); ‘slack_max’ is the upper bound of the slack variable and ‘capacity’ is the upper bound of the cumul variables. ‘name’ is the name used to reference the dimension; this name is used to get cumul and transit variables from the routing model. Returns false if a dimension with the same name has already been created (and doesn’t create the new dimension). Takes ownership of the callback ‘evaluator’. |
然後使用GetDimensionOrDie方法獲取dimension,並設定優化目標。注意在VRP問題中,路徑上給點賦的index和點實際的index不一樣,需要使用IndexToNode方法進行轉換才能得到實際的index。
3. 例子
先看一個簡單的例子:距離用曼哈頓距離,目標函式是最小化各車輛行駛距離的差別。可以對dimension使用SetGlobalSpanCostCoefficient方法可以獲得目標函式。global_span_cost = coefficient * (Max(dimension end value) - Min(dimension start value)).
程式碼如下:
from __future__ import print_function
from ortools.constraint_solver import pywrapcp
from ortools.constraint_solver import routing_enums_pb2
###########################
# Problem Data Definition #
###########################
def create_data_model():
"""Stores the data for the problem"""
data = {}
# Locations in block units
_locations = \
[(4, 4), # depot
(2, 0), (8, 0), # locations to visit
(0, 1), (1, 1),
(5, 2), (7, 2),
(3, 3), (6, 3),
(5, 5), (8, 5),
(1, 6), (2, 6),
(3, 7), (6, 7),
(0, 8), (7, 8)]
# Multiply coordinates in block units by the dimensions of an average city block, 114m x 80m,
# to get location coordinates.
data["locations"] = [(l[0] * 114, l[1] * 80) for l in _locations]
data["num_locations"] = len(data["locations"])
data["num_vehicles"] = 4
data["depot"] = 0
return data
#######################
# Problem Constraints #
#######################
def manhattan_distance(position_1, position_2):
"""Computes the Manhattan distance between two points"""
return (
abs(position_1[0] - position_2[0]) + abs(position_1[1] - position_2[1]))
def create_distance_callback(data):
"""Creates callback to return distance between points."""
_distances = {}
for from_node in range(data["num_locations"]):
_distances[from_node] = {}
for to_node in range(data["num_locations"]):
if from_node == to_node:
_distances[from_node][to_node] = 0
else:
_distances[from_node][to_node] = (
manhattan_distance(data["locations"][from_node],
data["locations"][to_node]))
def distance_callback(from_node, to_node):
"""Returns the manhattan distance between the two nodes"""
return _distances[from_node][to_node]
return distance_callback
def add_distance_dimension(routing, distance_callback):
"""Add Global Span constraint"""
distance = 'Distance'
maximum_distance = 3000 # Maximum distance per vehicle.
routing.AddDimension(
distance_callback,
0, # null slack
maximum_distance,
True, # start cumul to zero
distance)
distance_dimension = routing.GetDimensionOrDie(distance)
# Try to minimize the max distance among vehicles.
distance_dimension.SetGlobalSpanCostCoefficient(100)
###########
# Printer #
###########
def print_solution(data, routing, assignment):
"""Print routes on console."""
total_distance = 0
for vehicle_id in range(data["num_vehicles"]):
index = routing.Start(vehicle_id)
plan_output = 'Route for vehicle {}:\n'.format(vehicle_id)
distance = 0
while not routing.IsEnd(index):
plan_output += ' {} ->'.format(routing.IndexToNode(index))
previous_index = index
index = assignment.Value(routing.NextVar(index))
distance += routing.GetArcCostForVehicle(previous_index, index, vehicle_id)
plan_output += ' {}\n'.format(routing.IndexToNode(index))
plan_output += 'Distance of route: {}m\n'.format(distance)
print(plan_output)
total_distance += distance
print('Total distance of all routes: {}m'.format(total_distance))
########
# Main #
########
def main():
"""Entry point of the program"""
# Instantiate the data problem.
data = create_data_model()
# Create Routing Model
routing = pywrapcp.RoutingModel(
data["num_locations"],
data["num_vehicles"],
data["depot"])
# Define weight of each edge
distance_callback = create_distance_callback(data)
routing.SetArcCostEvaluatorOfAllVehicles(distance_callback)
add_distance_dimension(routing, distance_callback)
# Setting first solution heuristic (cheapest addition).
search_parameters = pywrapcp.RoutingModel.DefaultSearchParameters()
search_parameters.first_solution_strategy = (
routing_enums_pb2.FirstSolutionStrategy.PATH_CHEAPEST_ARC) # pylint: disable=no-member
# Solve the problem.
assignment = routing.SolveWithParameters(search_parameters)
if assignment:
print_solution(data, routing, assignment)
if __name__ == '__main__':
main()
輸出為:

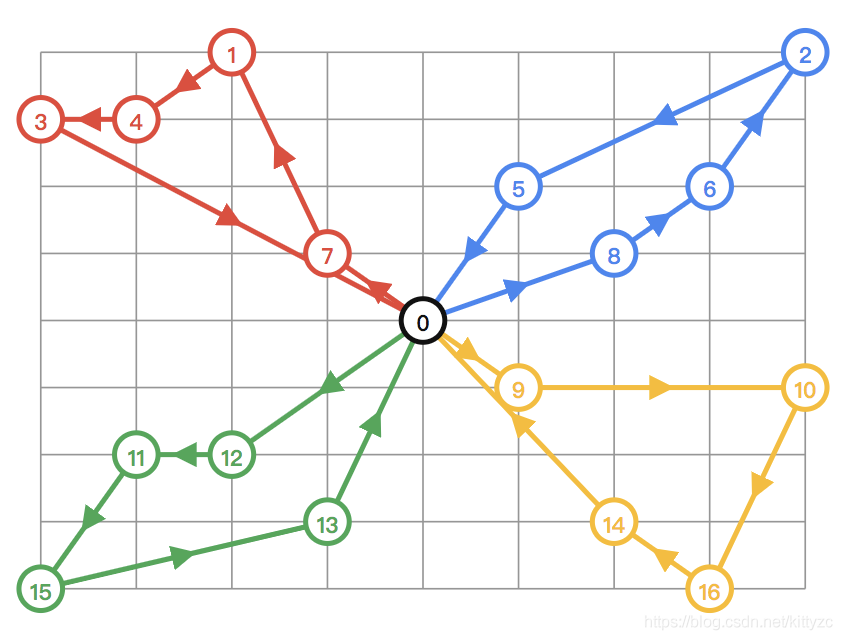
結果如下圖: