原文連結：https://zhuanlan.zhihu.com/p/21387326?refer=intelligentunit

內容列表：

• 簡介
• 損失函式視覺化
• 最優化
  • 策略#1：隨機搜尋
  • 策略#2：隨機區域性搜尋
  • 策略#3：跟隨梯度
• 梯度計算 譯者注：下篇起始處
  • 使用有限差值進行數值計算
  • 微分分析計算梯度
• 梯度下降
• 小結

梯度計算

計算梯度有兩種方法：一個是緩慢的近似方法（有限差值），但實現相對簡單。另一個方法（分析梯度法）計算迅速，結果精確，但是實現時容易出錯，且需要使用微分。現在對兩種方法進行介紹：

利用有限差值計算梯度

上節中的公式已經給出數值計算梯度的方法。下面程式碼是一個輸入為函式f和向量x，計算f的梯度的通用函式，它返回函式f在點x處的梯度：

def eval_numerical_gradient(f, x):
  """  
  一個f在x處的數值梯度法的簡單實現
  - f是隻有一個引數的函式
  - x是計算梯度的點
  """ 

  fx = f(x) # 在原點計算函式值
  grad = np.zeros(x.shape)
  h = 0.00001

  # 對x中所有的索引進行迭代
  it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
  while not it.finished:

    # 計算x+h處的函式值
    ix = it.multi_index
    old_value = x[ix]
    x[ix] = old_value + h # 增加h
    fxh = f(x) # 計算f(x + h)
    x[ix] = old_value # 存到前一個值中 (非常重要)

    # 計算偏導數
    grad[ix] = (fxh - fx) / h # 坡度
    it.iternext() # 到下個維度

  return grad
 

根據上面的梯度公式，程式碼對所有維度進行迭代，在每個維度上產生一個很小的變化h，通過觀察函式值變化，計算函式在該維度上的偏導數。最後，所有的梯度儲存在變數grad中。

實踐考量：注意在數學公式中，h的取值是趨近於0的，然而在實際中，用一個很小的數值（比如例子中的1e-5）就足夠了。在不產生數值計算出錯的理想前提下，你會使用盡可能小的h。還有，實際中用中心差值公式（centered difference formula）效果較好。細節可檢視wiki。

可以使用上面這個公式來計算任意函式在任意點上的梯度。下面計算權重空間中的某些隨機點上，CIFAR-10損失函式的梯度：

# 要使用上面的程式碼我們需要一個只有一個引數的函式
# (在這裡引數就是權重)所以也包含了X_train和Y_train
def CIFAR10_loss_fun(W):
  return L(X_train, Y_train, W)

W = np.random.rand(10, 3073) * 0.001 # 隨機權重向量
df = eval_numerical_gradient(CIFAR10_loss_fun, W) # 得到梯度

梯度告訴我們損失函式在每個維度上的斜率，以此來進行更新：

loss_original = CIFAR10_loss_fun(W) # 初始損失值
print 'original loss: %f' % (loss_original, )

# 檢視不同步長的效果
for step_size_log in [-10, -9, -8, -7, -6, -5,-4,-3,-2,-1]:
  step_size = 10 ** step_size_log
  W_new = W - step_size * df # 權重空間中的新位置
  loss_new = CIFAR10_loss_fun(W_new)
  print 'for step size %f new loss: %f' % (step_size, loss_new)

# 輸出:
# original loss: 2.200718
# for step size 1.000000e-10 new loss: 2.200652
# for step size 1.000000e-09 new loss: 2.200057
# for step size 1.000000e-08 new loss: 2.194116
# for step size 1.000000e-07 new loss: 2.135493
# for step size 1.000000e-06 new loss: 1.647802
# for step size 1.000000e-05 new loss: 2.844355
# for step size 1.000000e-04 new loss: 25.558142
# for step size 1.000000e-03 new loss: 254.086573
# for step size 1.000000e-02 new loss: 2539.370888
# for step size 1.000000e-01 new loss: 25392.214036

在梯度負方向上更新：在上面的程式碼中，為了計算W_new，要注意我們是向著梯度df的負方向去更新，這是因為我們希望損失函式值是降低而不是升高。

步長的影響：梯度指明瞭函式在哪個方向是變化率最大的，但是沒有指明在這個方向上應該走多遠。在後續的課程中可以看到，選擇步長（也叫作學習率）將會是神經網路訓練中最重要（也是最頭痛）的超引數設定之一。還是用矇眼徒步者下山的比喻，這就好比我們可以感覺到腳朝向的不同方向上，地形的傾斜程度不同。但是該跨出多長的步長呢？不確定。如果謹慎地小步走，情況可能比較穩定但是進展較慢（這就是步長較小的情況）。相反，如果想盡快下山，那就大步走吧，但結果也不一定盡如人意。在上面的程式碼中就能看見反例，在某些點如果步長過大，反而可能越過最低點導致更高的損失值。

————————————————————————————————————————

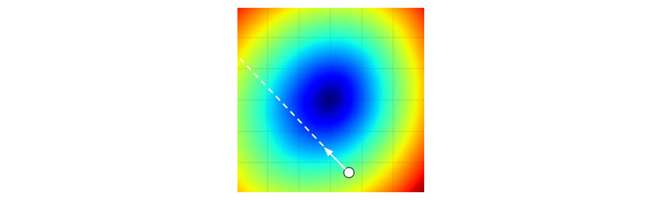
將步長效果視覺化的圖例。從某個具體的點W開始計算梯度（白箭頭方向是負梯度方向），梯度告訴了我們損失函式下降最陡峭的方向。小步長下降穩定但進度慢，大步長進展快但是風險更大。採取大步長可能導致錯過最優點，讓損失值上升。步長（後面會稱其為學習率）將會是我們在調參中最重要的超引數之一。

————————————————————————————————————————

效率問題：你可能已經注意到，計算數值梯度的複雜性和引數的量線性相關。在本例中有30730個引數，所以損失函式每走一步就需要計算30731次損失函式得到梯度（30730次f(x+h)和1次f(x)）。現代神經網路很容易就有上千萬的引數，因此這個問題只會越發嚴峻。顯然這個策略不適合大規模資料，我們需要更好的策略。

微分分析計算梯度

使用有限差值近似計算梯度比較簡單，但缺點在於終究只是近似（因為我們對於h值是選取了一個很小的數值，但真正的梯度定義中h趨向0的極限），且耗費計算資源太多。第二個梯度計算方法是利用微分來分析，能得到計算梯度的公式（不是近似），用公式計算梯度速度很快，唯一不好的就是實現的時候容易出錯。為了解決這個問題，在實際操作時常常將分析梯度法的結果和數值梯度法的結果作比較，以此來檢查其實現的正確性，這個步驟叫做梯度檢查。

用SVM的損失函式在某個資料點上的計算來舉例：

可以對函式進行微分。比如，對進行微分得到：（兩邊對求偏導得到）

譯者注：原公式中1為空心字型，嘗試\mathbb{}等多種方法仍無法實現，請知友指點。

其中是一個示性函式，如果括號中的條件為真，那麼函式值為1，如果為假，則函式值為0。雖然上述公式看起來複雜，但在程式碼實現的時候比較簡單：只需要計算沒有滿足邊界值的分類的數量（因此對損失函式產生了貢獻），然後乘以就是梯度了。注意，這個梯度只是對應正確分類的W的行向量的梯度，那些行的梯度是：

一旦將梯度的公式微分出來，程式碼實現公式並用於梯度更新就比較順暢了。

梯度下降

現在可以計算損失函式的梯度了，程式重複地計算梯度然後對引數進行更新，這一過程稱為梯度下降，他的普通版本是這樣的：

# 普通的梯度下降

while True:
  weights_grad = evaluate_gradient(loss_fun, data, weights)
  weights += - step_size * weights_grad # 進行梯度更新

這個簡單的迴圈在所有的神經網路核心庫中都有。雖然也有其他實現最優化的方法（比如LBFGS），但是到目前為止，梯度下降是對神經網路的損失函式最優化中最常用的方法。課程中，我們會在它的迴圈細節增加一些新的東西（比如更新的具體公式），但是核心思想不變，那就是我們一直跟著梯度走，直到結果不再變化。

小批量資料梯度下降（Mini-batch gradient descent）：在大規模的應用中（比如ILSVRC挑戰賽），訓練資料可以達到百萬級量級。如果像這樣計算整個訓練集，來獲得僅僅一個引數的更新就太浪費了。一個常用的方法是計算訓練集中的小批量（batches）資料。例如，在目前最高水平的卷積神經網路中，一個典型的小批量包含256個例子，而整個訓練集是多少呢？一百二十萬個。這個小批量資料就用來實現一個引數更新：

# 普通的小批量資料梯度下降

while True:
  data_batch = sample_training_data(data, 256) # 256個數據
  weights_grad = evaluate_gradient(loss_fun, data_batch, weights)
  weights += - step_size * weights_grad # 引數更新

這個方法之所以效果不錯，是因為訓練集中的資料都是相關的。要理解這一點，可以想象一個極端情況：在ILSVRC中的120萬個影象是1000張不同圖片的複製（每個類別1張圖片，每張圖片有1200張複製）。那麼顯然計算這1200張複製影象的梯度就應該是一樣的。對比120萬張圖片的資料損失的均值與只計算1000張的子集的資料損失均值時，結果應該是一樣的。實際情況中，資料集肯定不會包含重複影象，那麼小批量資料的梯度就是對整個資料集梯度的一個近似。因此，在實踐中通過計算小批量資料的梯度可以實現更快速地收斂，並以此來進行更頻繁的引數更新。

小批量資料策略有個極端情況，那就是每個批量中只有1個數據樣本，這種策略被稱為隨機梯度下降（Stochastic Gradient Descent 簡稱SGD），有時候也被稱為線上梯度下降。這種策略在實際情況中相對少見，因為向量化操作的程式碼一次計算100個數據 比100次計算1個數據要高效很多。即使SGD在技術上是指每次使用1個數據來計算梯度，你還是會聽到人們使用SGD來指代小批量資料梯度下降（或者用MGD來指代小批量資料梯度下降，而BGD來指代則相對少見）。小批量資料的大小是一個超引數，但是一般並不需要通過交叉驗證來調參。它一般由儲存器的限制來決定的，或者乾脆設定為同樣大小，比如32，64，128等。之所以使用2的指數，是因為在實際中許多向量化操作實現的時候，如果輸入資料量是2的倍數，那麼運算更快。

小結

————————————————————————————————————————

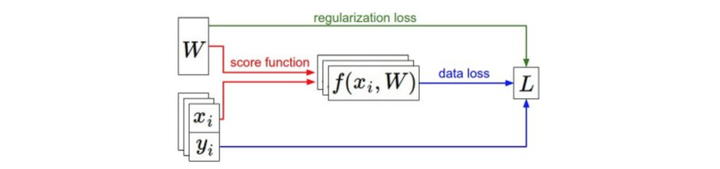
資訊流的總結圖例。資料集中的(x,y)是給定的。權重從一個隨機數字開始，且可以改變。在前向傳播時，評分函式計算出類別的分類評分並存儲在向量f中。損失函式包含兩個部分：資料損失和正則化損失。其中，資料損失計算的是分類評分f和實際標籤y之間的差異，正則化損失只是一個關於權重的函式。在梯度下降過程中，我們計算權重的梯度（如果願意的話，也可以計算資料上的梯度），然後使用它們來實現引數的更新。

—————————————————————————————————————————

在本節課中：

• 將損失函式比作了一個高維度的最優化地形，並嘗試到達它的最底部。最優化的工作過程可以看做一個蒙著眼睛的徒步者希望摸索著走到山的底部。在例子中，可見SVM的損失函式是分段線性的，並且是碗狀的。

• 提出了迭代優化的思想，從一個隨機的權重開始，然後一步步地讓損失值變小，直到最小。

• 函式的梯度給出了該函式最陡峭的上升方向。介紹了利用有限的差值來近似計算梯度的方法，該方法實現簡單但是效率較低（有限差值就是h，用來計算數值梯度）。

• 引數更新需要有技巧地設定步長。也叫學習率。如果步長太小，進度穩定但是緩慢，如果步長太大，進度快但是可能有風險。

• 討論權衡了數值梯度法和分析梯度法。數值梯度法計算簡單，但結果只是近似且耗費計算資源。分析梯度法計算準確迅速但是實現容易出錯，而且需要對梯度公式進行推導的數學基本功。因此，在實際中使用分析梯度法，然後使用梯度檢查來檢查其實現正確與否，其本質就是將分析梯度法的結果與數值梯度法的計算結果對比。

• 介紹了梯度下降演算法，它在迴圈中迭代地計算梯度並更新引數。

預告：這節課的核心內容是：理解並能計算損失函式關於權重的梯度，是設計、訓練和理解神經網路的核心能力。下節中，將介紹如何使用鏈式法則來高效地計算梯度，也就是通常所說的反向傳播（backpropagation）機制。該機制能夠對包含卷積神經網路在內的幾乎所有型別的神經網路的損失函式進行高效的最優化。

最優化筆記全文翻譯完。