《資料結構》09-排序1 排序
阿新 • • 發佈:2018-11-25
題目
給定N個(長整型範圍內的)整數,要求輸出從小到大排序後的結果。
本題旨在測試各種不同的排序演算法在各種資料情況下的表現。各組測試資料特點如下:
- 資料1:只有1個元素;
- 資料2:11個不相同的整數,測試基本正確性;
- 資料3:10 個隨機整數;
- 資料4:10 個隨機整數;
- 資料5:10 個隨機整數;
- 資料6:10 個順序整數;
- 資料7:10 個逆序整數;
- 資料8:10 個基本有序的整數;
- 資料9:10 個隨機正整數,每個數字不超過1000。
輸入格式:
輸入第一行給出正整數N(≤10
),隨後一行給出N個(長整型範圍內的)整數,其間以空格分隔。
輸出格式:
在一行中輸出從小到大排序後的結果,數字間以1個空格分隔,行末不得有多餘空格。
輸入樣例:
11
4 981 10 -17 0 -20 29 50 8 43 -5
輸出樣例:
-20 -17 -5 0 4 8 10 29 43 50 981
分析
基本就是各種排序演算法的測試了
- 氣泡排序
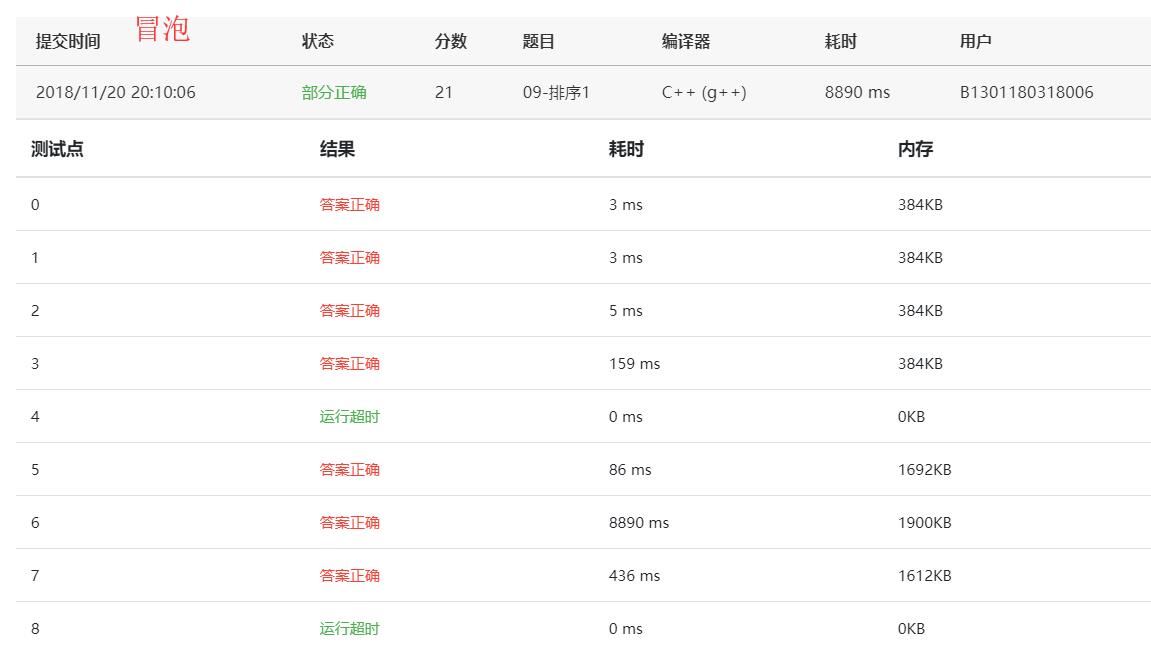
- 插入排序

- 原始希爾排序

- Hibbard增量序列希爾排序

- Sedgewick增量序列雜湊排序

- 堆排序

- STL實現堆排序

- 遞迴歸併排序
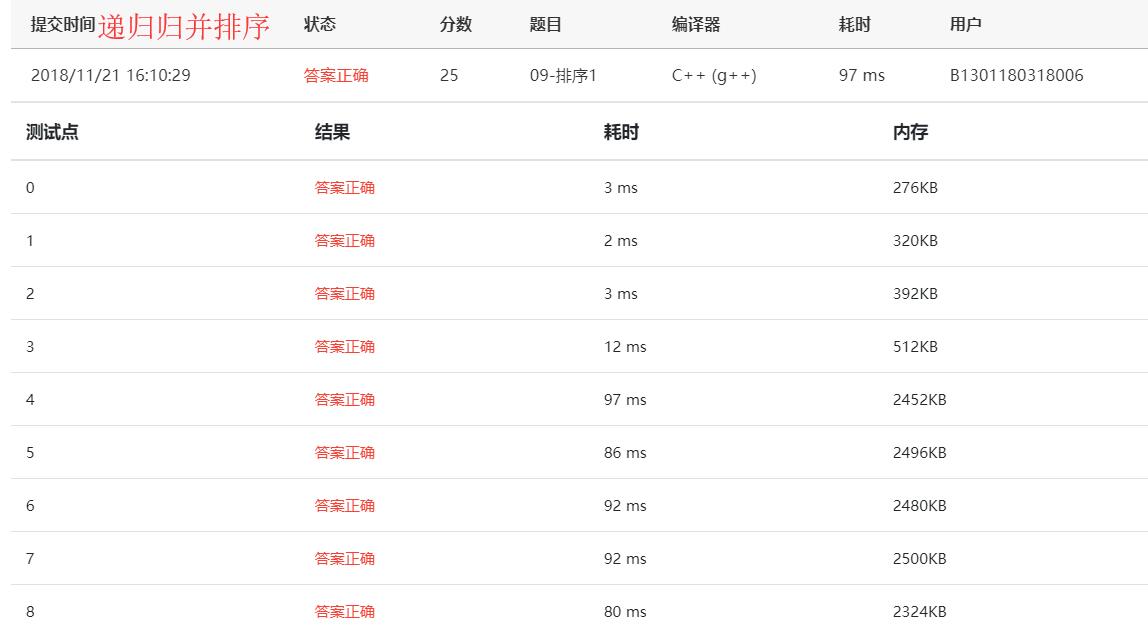
- 非遞迴歸併排序

- 快速排序

#include<iostream>
#include<algorithm>
#include<queue>
using namespace std;
// 氣泡排序
void Bubble_sort(long A[],int N){
for(int i=0;i<N-1;i++){ // N-1次冒泡
bool flag = false; // 驗證是否互動過
for(int j=0;j<N-i-1;j++){
if(A[j+1] < A[j]){
flag = true;
swap(A[j],A[j+1]);
}
}
// 已經有序
if(!flag)
break;
}
}
// 插入排序
void Insertion_sort(long A[],int N){
for(int i=1;i<N;i++){ // 第一個已經成序
long tmp = A[i];
int j=i;
for(;tmp<A[j-1] && j>0;j--)
A[j] = A[j-1];
A[j] = tmp;
}
}
// 原始希爾排序
void shell_sort(long A[],int N){
for(int D=N/2;D>0;D/=2){
for(int p=D;p<N;p++){
long tmp = A[p];
int k=p;
for(;k>=D && tmp<A[k-D] ;k-=D) // j>=D 在前,因為也許 A[j-D]已經越界
A[k] = A[k-D];
A[k] = tmp;
}
}
}
// Hibbard增量序列希爾排序
void Hibbard_shell_sort(long A[],int N){
int add[]={32767,16383,8191,4095,2047,1023,511,255,127,63,31,15,7,3,1,0};
int i=0;
for(int D=add[i];D>0;D=add[++i]){
for(int p=D;p<N;p++){
long tmp = A[p];
int k=p;
for(;k>=D && tmp<A[k-D] ;k-=D) // j>=D 在前,因為也許 A[j-D]已經越界
A[k] = A[k-D];
A[k] = tmp;
}
}
}
// Sedgewick增量序列雜湊排序
void Sedgewick_shell_sort(long A[],int N){
int add[]= {587521,260609,146305,64769,36289,16001,8929,3905,2161,929,505,209,109,41,19,5,1,0};
int i=0;
for(int D=add[i];D>0;D=add[++i]){
for(int p=D;p<N;p++){
long tmp = A[p];
int k = p;
for(;k>=D && tmp<A[k-D];k-=D)
A[k] = A[k-D];
A[k] = tmp;
}
}
}
/***************堆排序開始***************/
// 調整成最大堆
void PrecDown(long A[],int i,int N){
int parent,child;
long tmp = A[i];
// 從 0 開始存,所以關係有變化
for(parent = i;parent*2+1<N;parent = child){
child = parent*2+1;
if((child!=N-1) && (A[child] < A[child+1]))
child++;
if(A[child] <= tmp)
break;
else
A[parent] = A[child];
}
A[parent] = tmp;
}
// 堆排序
void Heap_sort(long A[],int N){
// 先調整成最大堆
for(int i=N/2;i>=0;i--)
PrecDown(A,i,N);
for(int i=N-1;i>0;i--){
swap(A[0],A[i]); // 每次把當前最大堆根元素選擇出來
PrecDown(A,0,i); // 再次調整最大堆
}
}
/***************堆排序結束***************/
/***************stl堆排序開始***************/
priority_queue<long,vector<long>,less<long> > q; // 定義一個最大堆
void STL_Heap_sort(long A[],int N){
// 資料讀入最大堆
for(int i=0;i<N;i++)
q.push(A[i]);
// 依次出隊
for(int i=N-1;i>=0;i--){
A[i] = q.top();
q.pop();
}
}
/***************stl堆排序結束***************/
/***************遞迴歸併排序開始***************/
/*
// 歸併實現
void Merge(long A[],long tmpA[],int L,int R,int RightEnd){
// L = 左邊元素開始位置 ,R = 右邊元素開始位置 ,RightEnd = 右邊結束終點位置
int NumSize = RightEnd-L+1; // 元素個數
int LeftEnd = R-1; // 左邊元素終點位置
int tmp = L; // tmp 陣列開始位置
while( L <= LeftEnd && R <= RightEnd ){
if(A[L] <= A[R]) // 從小到大排序,選小的
tmpA[tmp++] = A[L++];
else
tmpA[tmp++] = A[R++];
}
// 也許左沒走完
while( L <= LeftEnd )
tmpA[tmp++] = A[L++];
// 也許右邊沒走完
while( R <= RightEnd)
tmpA[tmp++] = A[R++];
// 再導回 A ,tmp此時已經越界,所以要先減再用
for(int i=0;i<NumSize;i++)
A[RightEnd--] = tmpA[--tmp];
}
// 分治
void Msort(long A[],long tmpA[],int L,int RightEnd){
if(L < RightEnd){
int center = ( L + RightEnd )/2;
Msort(A,tmpA,L,center);
Msort(A,tmpA,center+1,RightEnd);
Merge(A,tmpA,L,center+1,RightEnd);
}
}
void Merge_sort(long A[],int N){
long tmpA[N];
Msort(A,tmpA,0,N-1);
}
*/
/***************遞迴歸併排序結束***************/
/***************非遞迴歸併排序開始***************/
// 歸併實現 ,最後不把元素倒回A
void Merge1(long A[],long tmpA[],int L,int R,int RightEnd){
// L = 左邊元素開始位置 ,R = 右邊元素開始位置 ,RightEnd = 右邊結束終點位置
int NumSize = RightEnd-L+1; // 元素個數
int LeftEnd = R-1; // 左邊元素終點位置
int tmp = L; // tmp 陣列開始位置
while( L <= LeftEnd && R <= RightEnd ){
if(A[L] <= A[R]) // 從小到大排序,選小的
tmpA[tmp++] = A[L++];
else
tmpA[tmp++] = A[R++];
}
// 也許左沒走完
while( L <= LeftEnd )
tmpA[tmp++] = A[L++];
// 也許右邊沒走完
while( R <= RightEnd)
tmpA[tmp++] = A[R++];
}
// 一趟歸併
void Merge_pass(long A[],long tmpA[],int N,int length){
int i;
// 每 2*length 一個單元歸併
for(i=0;i<N-2*length;i+=2*length)
Merge1(A,tmpA,i,i+length,i+2*length-1);
// 處理剩餘不足一個單元的值
if(i+length < N) // 剩下兩個子列,左邊夠,右邊不夠
Merge1(A,tmpA,i,i+length,N-1);
else // 剩下一個子列,左邊都不夠
for(int j=i;j<N;j++)
tmpA[j] = A[j];
}
void Merge_sort(long A[],int N){
int length = 1;
long tmpA[N];
// 保證每次兩趟歸併,最終結果一定存在 A中
while(length < N){
Merge_pass(A,tmpA,N,length);
length *=2;
Merge_pass(tmpA,A,N,length);
length *=2;
}
}
/***************非遞迴歸併排序結束***************/
/*********************快速排序開始*******************************************/
// 選主元
long getPivot(long A[],int L,int R){
int center = (L+R)/2;
if(A[R] < A[center])
swap(A[R],A[center]);
if(A[R] < A[L])
swap(A[R],A[L]);
if(A[center] < A[L])
swap(A[center],A[L]);
swap(A[center],A[R-1]);
return A[R-1];
}
void QucikSort(long A[],int Left,int Right){
int cutoff = 50;
if( cutoff <= Right - Left ){ // 如果規模大用快排
int pivot = getPivot(A,Left,Right);
int i = Left;
int j = Right-1;
for(;;){
// 從前往後找比 pivot 小的
while(A[++i] < pivot);
// 從後往前找比 pivot 大的
while(A[--j] > pivot);
if(j <= i)
break;
swap(A[i],A[j]);
}
// 將主元放在合適位置
swap(A[i],A[Right-1]);
QucikSort(A,Left,i-1);
QucikSort(A,i+1,Right);
}else // 否則用插入排序
Insertion_sort(A+Left,Right-Left+1);
}
void Quick_sort(long A[],int N){
QucikSort(A,0,N-1);
}
/*********************快速排序結束**********************************/
int main(){
int N;
cin>>N;
long A[N];
for(int i=0;i<N;i++)
cin>>A[i];
Merge_sort(A,N);
for(int i=0;i<N;i++){
if(i)
cout<<" ";
cout<<A[i];
}
return 0;
}
