題意： 經典的遞迴題，

要求：除了要求 橫豎都填滿 1~9外， 每個3*3也都要求滿足 1~9 

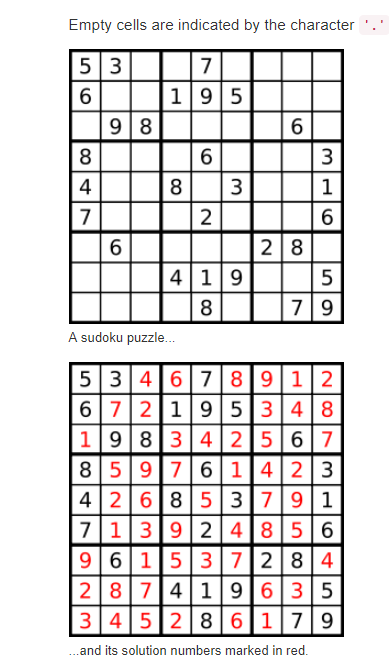
36. 陣列可以部分填充， 問是否一個有效的 sudoku. 

寫了個好燒腦的 四重迴圈來check 3*3 的部分。  重點在於 用陣列作為hash 。 然後對於 check 3*3 部分， 其實就是9個小方塊，  9個小方塊 定點座標為 [0 0] [0 3] [06] [3 0] [3 3 ] [3 6] [6 0] [ 6 3] [6 6] ，每個頂點遞增為橫豎 遞增都 3 ， 因此寫了個二重迴圈來控制頂點座標：

for(int i=0; i<9; i= i+3

class Solution {
    public boolean isValidSudoku(char[][] board) {
        
        boolean[][] map_row = new boolean[10][10];
        boolean[][] map_col = new boolean[10][10];       
        //check row and col
        for(int i=0; i<9; i++){
            
 
for(int j=0; j<9; j++){
                if(board[i][j] != '.'){
                    int num = board[i][j] - '0';
                    if(map_row[i][num]) return false;
                    map_row[i][num] = true;
                    if(map_col[num][j]) return false;
                    map_col[num][j] 
 
= true;
                }
            }
        }
        
        //check 3*3
        for(int i=0; i<9; i= i+3){
            for(int j=0; j<9; j=j+3) {
                boolean[] map = new boolean[10];
                for(int k=0; k<3; k++){
                    for(int t=0; t<3; t++){
                        int num = board[k+i][t+j] - '0';
                        if(board[k+i][t+j] != '.'){
                            if(map[num]) return false;
                            map[num] = true;
                        }
                    }
                    
                }
            }
        }
     return true;
    }
}

37 終於回到數獨問題經典 backtracking 了。 

class Solution {
    public void solveSudoku(char[][] board) {
        
     List<Integer> indexs = new ArrayList<>();   
        
      for(int i=0; i<9; i++)
            for(int j=0; j<9; j++)
                if(board[i][j] == '.')
                    indexs.add(i*9+j);
    
     dfs(board, indexs,0) ;
  }
    
    private boolean dfs(char[][] board, List<Integer> indexs, int depth){
        
        if(depth == indexs.size()) {
            return true;
        }
    
        boolean flag = false;
        int i, j=0;
        int index =  indexs.get(depth);
        i = index/9;
        j = index%9;
        
        for(int n=1; n<=9; n++){
           if(isValid(board, (char)(n+'0'), i, j )  ){
               board[i][j] = (char)(n+'0');
               if (dfs(board,indexs, depth+1)) return true;    //如果滿足條件就直接return 了
           } 
        }
        
        // 如果迴圈結束了，說明 for 迴圈裡 沒有成功， 所以 此位置嘗試 1~9 均失敗，所以 back tracking 回去。
        board[i][j] = '.'; 
        return false;
    }
    
    private boolean isValid(char[][] board, char num, int x,int y){

        int i=0, j=0; 
        for( i=0; i<9; i++){
            if( board[x][i] == num) return false;
        }
        for( j=0; j<9; j++){
            if( board[j][y] == num) return false;
        }
        
        for (i = 3 * (x / 3); i < 3 * (x / 3 + 1); i++)
            for (j = 3 * (y / 3); j < 3 * (y / 3 + 1); j++)
                if (i!=x && j!= y &&board[i][j] == num)
                    return false;
   
        return true;
    }
}