矩陣與張量的區別
關於矩陣和張量的區別有些人可能不太清楚,看了這篇文章相信你會很明白了。
矩陣是由括號括起的n×m(例如,3×3)個數字的網格。我們可以加上和減去相同大小的矩陣,只要大小相容((n×m)×(m×p)= n×p),就將一個矩陣與另一個矩陣相乘,以及可以將整個矩陣乘以常數。向量是一個只有一行或一列的矩陣。我們可以對任何矩陣進行一系列數學運算。
不過,基本的思想是,矩陣只是一個二維的數字網格。
張量通常被認為是一個廣義矩陣。也就是說,它可以是1-D矩陣(一個向量實際上就是一個張量),3-D矩陣(類似於一個數字的立方),甚至是0-D矩陣(單個數字),或者一個更難形象化的高維結構。張量的維數叫做它的秩
但是這個描述忽略了張量最重要的性質!
張量是一個數學實體,它存在於一個結構中並與其他數學實體相互作用。如果以常規方式轉換結構中的其他實體,那麼張量必須服從一個相關的變換規則。
張量的這種“動態”特性是將其與單純矩陣區分開來的關鍵。它是一個團隊成員,當一個影響到所有成員的轉換被引入時,它的數值會隨著隊友的數值而變化。
任何秩-2張量都可以表示為一個矩陣,但並不是每個矩陣都是秩-2張量。張量矩陣表示的數值取決於整個系統應用了什麼變換規則。
上面的介紹可能有些繞口。但是我們可以通過一個小例子來說明它是如何工作的。這個問題是在一個深度學習研討會上提出的,所以讓我們看一下該領域的一個簡單例子。
假設我在神經網路中有一個隱藏的3個節點層。資料流入它們,通過它們的ReLU函式,然後彈出一些值。對於確定性,我們分別得到2.5,4和1.2。 我們可以將這些節點的輸出表示為向量:
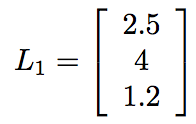
假設有另外一層3個節點。第一層的3個節點中的每個節點都有一個權重,該權重與其對接下來3個節點的輸入相關聯。那麼,將這些權重寫為3×3矩陣的條目將是非常方便的。假設我們已經對網路進行了多次更新,並得到了權重(本例中半隨機選擇)。
在這裡,一行的權值都到下一層的同一個節點,而某一列的權值都來自第一層的同一個節點。例如,輸入節點1對輸出節點3的權值是0.2(第3行,第1列)。 我們可以通過將權重矩陣乘以輸入向量來計算饋入下一層節點的總值,
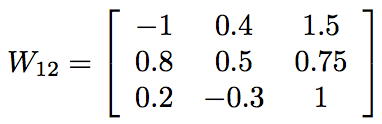
這裡有一個圖。資料從左到右流動。
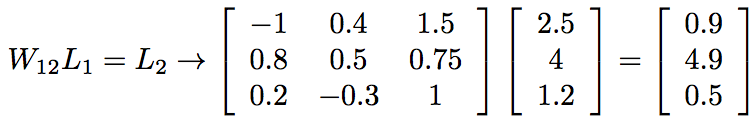
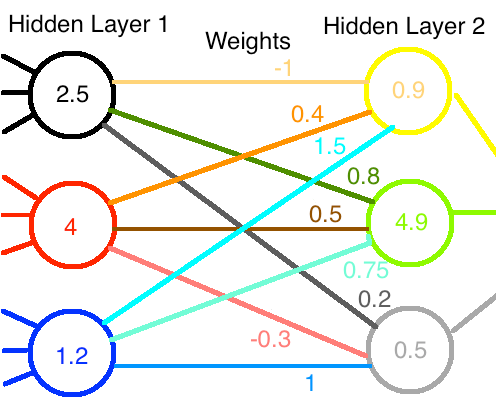
到目前為止,我們所看到的只是矩陣和向量的一些簡單操作。
但是,假設我想對每個神經元進行干預並使用自定義啟用函式。一種簡單的方法是從第一層重新縮放每個ReLU函式。在本例中,假設我將第一個節點向上擴充套件2倍,保留第二個節點,將第三個節點向下擴充套件1/5。這將改變這些函式的圖形如下圖所示:
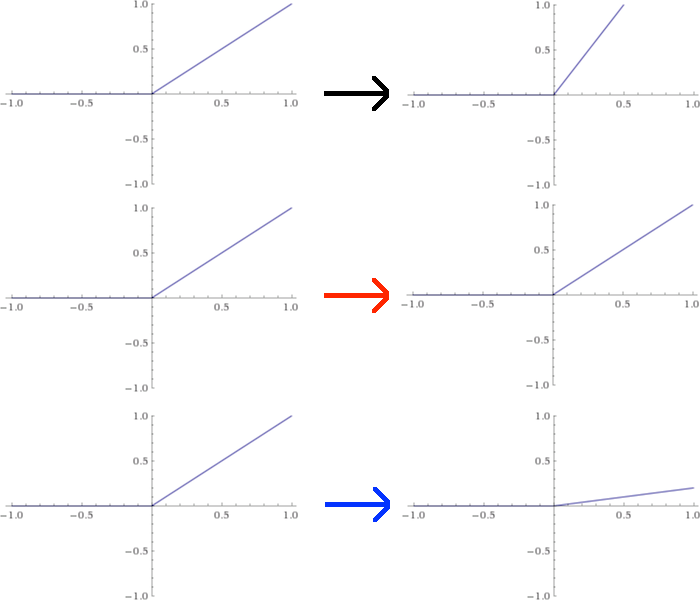
這種修改的效果是將第一層生成的值分別乘以2、1和1/5。等於L1乘以一個矩陣A,

現在,如果這些新值通過原來的權值網路被輸入,我們得到完全不同的輸出值,如圖所示:
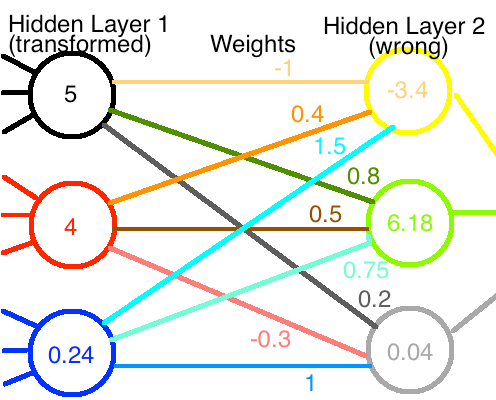
如果神經網路之前運作正常,我們現在就把它破壞了。我們必須重新進行訓練以恢復正確的重量。
或者我們會嗎?
第一個節點的值是之前的兩倍。 如果我們將所有輸出權值減少1/2,則它對下一層的淨貢獻不變。我們沒有對第二個節點做任何處理,所以我們可以不考慮它的權值。最後,我們需要將最後一組權值乘以5,以補償該節點上的1/5因子。從數學上講,這相當於使用一組新的權值,我們通過將原權矩陣乘以A的逆矩陣得到:
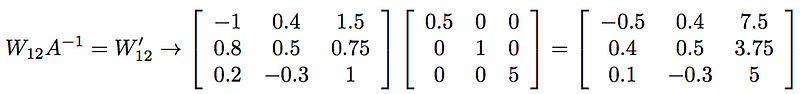
如果我們將第一層的修改後的輸出與修改後的權值結合起來,我們最終會得到到達第二層的正確值:
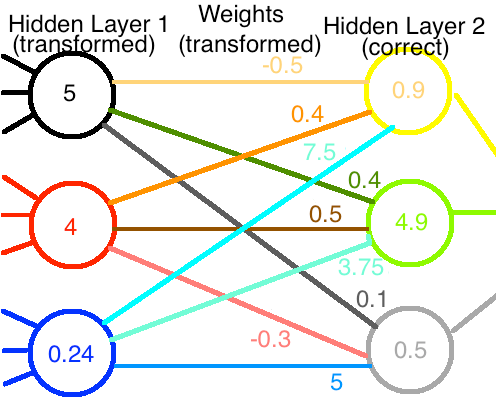
太好了!儘管我們做出了最大努力,但網路仍在重新運作!
好了,我們已經學了很多數學了,讓我們回顧一下。
當我們把節點的輸入,輸出和權值看作固定的量時,我們稱它們為向量和矩陣,並用它完成。
但是,一旦我們開始用其中一個向量進行修復,以常規方式對其進行轉換,我們就必須通過相反的方式轉換權值來進行補償。這個附加的、整合的結構將單純的數字矩陣提升為一個真正的張量物件。
事實上,我們可以進一步描述它的張量性質。如果我們把對節點的變化稱為協變(即,隨著節點的變化而乘以A),那麼權值就變成了一個逆變張量(具體來說,對節點變化,乘以A的倒數而不是A本身)。張量可以在一個維度上是協變的,在另一個維度上是逆變的,但那是另外的事了。
這就是矩陣和張量之間的本質的區別。
