講解一下，我的演算法，基於幾何圖形搭建的障礙物地圖的演算法，一般使用在移動機器人路徑規劃或者地圖構建的領域，演算法是由matlab編寫的，程式碼會提供下載連結，關於程式碼的講解，現在開始。

1   基於幾何圖形搭建的障礙物地圖的演算法構建的障礙物圖形如下圖1所示：

                                                                                                圖1

其中黑色線條圍成的藍色區域，即為障礙物區域，這些基本的幾何圖形構成了障礙物區域，本演算法主要採用的是線性規劃的原理構建的障礙物資訊。如下所示，

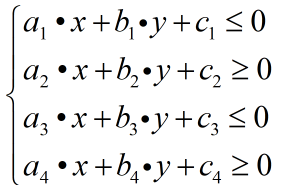
由這四條 直線構成的圖形所圍成的區域可以通過我寫的Barrier函式完成障礙物區域的構建，你只需要先計算出構成你的障礙物圖形的每一條邊的直線方程即可，程式碼如下，

function  [numbarrier,quadrantBarrier] = Barrier( x,y,confine)
%構建障礙物區域
%輸入引數
% x----x軸座標
% y----y軸座標
% confine----地圖邊界
% 輸出引數
% orderBarrier----返回改點在第幾象限
% numbarrier----該象限第幾個障礙物,若numbarrier == 32代表到達地圖邊界,若numbarrier==0代表不在障礙物區域,numbarrier = 16,代表座標軸
%%

quadrant = 0;
numbarrier = 0;
quadrantBarrier = 0;
%判斷點在哪一個象限
if x >= 0 && y >= 0
    quadrant = 1;
elseif x < 0 && y > 0
    quadrant = 2;
elseif x < 0 && y < 0
    quadrant = 3;
else
    quadrant = 4;
end

switch (quadrant)
    case 1
        quadrantBarrier = 1; %第一象限
        if x <= 0||y <= 0
            numbarrier = 16;
        end
        if x >= confine || y >= confine
             numbarrier = 32; 
        end
        if x-2-y <= 0 && 0.5-y <= 0 && -x+2-y <= 0 && y-x-1 <= 0 && y-2.5 <= 0 && y+x-5 <= 0%第一象限障礙物區，這些方程即為構成該象限的障礙物區域方程，你需要在這裡做變動定製成你的直線方程
            numbarrier = 1;%返回1表示在障礙物區域
        end

    case 2
        quadrantBarrier = 2; %第二象限
        if x >= 0||y <= 0
            numbarrier = 16;
        end
        if x <= -confine || y >= confine
             numbarrier = 32; 
        end
%%
% 對於組合圖形 1 的描述
        if x+2.5-y <= 0 && -x-1.5-y <= 0 && y-x/3-13/6 <= 0
            numbarrier = 1;
        end
%         if y+x+1.5 <= 0 && x+4.5-y <= 0 && y-2*x-8.5 <= 0
%              numbarrier = 1;
%         end
        if -x-1.5-y <= 0 && y-2*x-8.5 <= 0 && y+x+0.5 <= 0 && x/3+13/6-y <= 0
             numbarrier = 1;
        end
%
    case 3
        quadrantBarrier = 3; %第三象限
        if x >= 0||y >= 0
            numbarrier = 16;
        end
        if x <= -confine || y <= -confine
             numbarrier = 32; 
        end
%%
% 對於組合圖形 1 的描述        
        if x+1 <= 0 && -3.5-x <= 0 && y+1 <= 0 && -1.5-y <= 0
            numbarrier = 1;
        end
        if x+1.5 <= 0 && -3.5-x <= 0 && y+1.5 <= 0 && -2-y <= 0
            numbarrier = 1;
        end
        if x+1.5 <= 0 && -2.5-x <= 0 && y+2 <= 0 && -2.5-y <= 0 
             numbarrier = 1;
        end
%
    case 4
        quadrantBarrier = 4; %第四象限
        if x <= 0||y >= 0
            numbarrier = 16;
        end
        if x >= confine || y <= -confine
             numbarrier = 32; 
        end
        if 1.5*x-5-y <= 0 && -x-y <=0 && y+0.5 <=0
            numbarrier = 1;
        end
end

end

 

由以上演算法可知，所有在numbarrier=1處的判斷條件中的直線方程，你都因該改成你自己構建障礙物的方程。

2    障礙物區域搭建好了，還需要將該區域畫出來

通過我寫的drawMap函式，輸入地圖的邊界就能畫出第1節中的障礙物區域圖，和圖1的效果一樣。程式碼如下所示，

function   drawMap(x_neg,x_pos,y_neg,y_pos)
%輸入引數：
% x_neg----x軸負界
% x_pos----x軸正界
% y_neg----y軸負界
% y_pos----x軸正界

%畫出y = 0曲線
x0_1 = x_neg:1:x_pos;
y0_1 = 0.*x0_1;
plot(x0_1,y0_1,'k--');

hold on;

%畫出x = 0曲線
y0_2 = y_neg:1:y_pos;
x0_2 = 0.*y0_2;
plot(x0_2,y0_2,'k--');
hold on;

% scatter(0,0,'MarkerEdgeColor',[1 0 0],'MarkerFaceColor',[1 0 0], 'LineWidth',1);%畫出(0,0)


%%
%繪製障礙物區域
syms x y

%描述障礙物不等式組
%第一象限
%%
%這也是一種畫法，但是很詭異
% v1_1 = cat(6,x-2-y,0.5-y,-x+2-y,y-x-1,y-2.5,y+x-5);%全部化成<=0的不等式
% v1_1 = max(v1_1,[],6);
% contourf(x,y,-v1_1,[0,0]);
% colormap(display_color);
%%
[x1_1,y1_1] = solve(x-2-y == 0,0.5-y == 0,x,y);
[x1_2,y1_2] = solve(0.5-y == 0,-x+2-y == 0,x,y);
[x1_3,y1_3] = solve(-x+2-y == 0,y-x-1 == 0,x,y);
[x1_4,y1_4] = solve(y-x-1 == 0,y-2.5 == 0,x,y);
[x1_5,y1_5] = solve(y-2.5 == 0,y+x-5 == 0,x,y);
[x1_6,y1_6] = solve(x-2-y == 0,y+x-5 == 0,x,y);

plot(x1_1,y1_1,x1_2,y1_2,x1_3,y1_3,x1_4,y1_4,'-b',x1_5,y1_5,x1_6,y1_6,'-b');

X1_1 = [x1_1,x1_2,x1_3,x1_4,x1_5,x1_6,x1_1];
Y1_1 = [y1_1,y1_2,y1_3,y1_4,y1_5,y1_6,y1_1];
h = fill(X1_1,Y1_1,'c');

hold on;

%第二象限
%---------------------障礙物2_1的第一部分--------------------------
[x2_1,y2_1] = solve(x+2.5-y== 0,-x-1.5-y == 0,x,y);
[x2_2,y2_2] = solve(-x-1.5-y == 0,y-x/3-13/6 == 0,x,y);
[x2_3,y2_3] = solve(y-x/3-13/6 == 0,x+2.5-y == 0,x,y);

plot(x2_1,y2_1,x2_2,y2_2,x2_3,y2_3);

X2_1_1= [x2_1,x2_2,x2_3,x2_1];
Y2_1_1 = [y2_1,y2_2,y2_3,y2_1];
h = fill(X2_1_1,Y2_1_1,'c');

%---------------------障礙物2_1的第二部分--------------------------
% [x2_4,y2_4] = solve(y+x+1.5 == 0,x+4.5-y == 0,x,y);
% [x2_5,y2_5] = solve(x+4.5-y == 0,y-2*x-8.5 == 0,x,y);
% [x2_6,y2_6] = solve(y-2*x-8.5 == 0,y+x+1.5 == 0,x,y);
% 
% plot(x2_4,y2_4,x2_5,y2_5,x2_6,y2_6);
% 
% X2_1_2 = [x2_4,x2_5,x2_6,x2_4];
% Y2_1_2 = [y2_4,y2_5,y2_6,y2_4];
% h = fill(X2_1_2,Y2_1_2,'c');
%---------------------障礙物2_1的第三部分--------------------------
[x2_7,y2_7] = solve(-x-1.5-y == 0,y-2*x-8.5 == 0,x,y);
[x2_8,y2_8] = solve(y-2*x-8.5 == 0,y+x+0.5 == 0,x,y);
[x2_9,y2_9] = solve(y+x+0.5 == 0,x/3+13/6-y == 0,x,y);
[x2_10,y2_10] = solve(x/3+13/6-y == 0,-x-1.5-y == 0,x,y);

plot(x2_7,y2_7,x2_8,y2_8,x2_9,y2_9,x2_10,y2_10);

X2_1_3 = [x2_7,x2_8,x2_9,x2_10,x2_7];
Y2_1_3 = [y2_7,y2_8,y2_9,y2_10,y2_7];
h = fill(X2_1_3,Y2_1_3,'c');

% %第三象限

% -----------------障礙物3_1第一部分----------
[x3_1,y3_1] = solve(x+1 == 0,y+1 == 0,x,y);
[x3_2,y3_2] = solve(y+1 == 0,3.5+x == 0,x,y);
[x3_3,y3_3] = solve(3.5+x == 0,1.5+y == 0,x,y);
[x3_4,y3_4] = solve(1.5+y == 0,x+1 == 0,x,y);

plot(x3_1,y3_1,x3_2,y3_2,x3_3,y3_3,x3_4,y3_4);

X3_1_1 = [x3_1,x3_2,x3_3,x3_4,x3_1];
Y3_1_1 = [y3_1,y3_2,y3_3,y3_4,y3_1];
h = fill(X3_1_1,Y3_1_1,'c');

% -----------------障礙物3_1第二部分----------
[x3_5,y3_5] = solve(x+1.5 == 0,y+1.5 == 0,x,y);
[x3_6,y3_6] = solve(y+1.5 == 0,3.5+x == 0,x,y);
[x3_7,y3_7] = solve(3.5+x == 0,2+y == 0,x,y);
[x3_8,y3_8] = solve(2+y == 0,x+1.5 == 0,x,y);

plot(x3_5,y3_5,x3_6,y3_6,x3_7,y3_7,x3_8,y3_8);

X3_1_2 = [x3_5,x3_6,x3_7,x3_8,x3_5];
Y3_1_2 = [y3_5,y3_6,y3_7,y3_8,y3_5];
h = fill(X3_1_2,Y3_1_2,'c');

% -----------------障礙物3_1第三部分----------
[x3_9,y3_9] = solve(x+1.5 == 0,y+2 == 0,x,y);
[x3_10,y3_10] = solve(y+2 == 0,2.5+x == 0,x,y);
[x3_11,y3_11] = solve(2.5+x == 0,2.5+y == 0,x,y);
[x3_12,y3_12] = solve(2.5+y == 0,x+1.5 == 0,x,y);

plot(x3_9,y3_9,x3_10,y3_10,x3_11,y3_11,x3_12,y3_12);

X3_1_3 = [x3_9,x3_10,x3_11,x3_12,x3_9];
Y3_1_3 = [y3_9,y3_10,y3_11,y3_12,y3_9];
h = fill(X3_1_3,Y3_1_3,'c');

% 第四象限
%4-1代表第四象限第一個障礙物，以此類推
[x4_1,y4_1] = solve(1.5*x-5-y == 0,-x-y == 0,x,y);
[x4_2,y4_2] = solve(-x-y == 0,y+0.5 == 0,x,y);
[x4_3,y4_3] = solve(1.5*x-5-y == 0,y+0.5 == 0,x,y);

plot(x4_1,y4_1,x4_2,y4_2,x4_3,y4_3);

X4_1 = [x4_1,x4_2,x4_3,x4_1];
Y4_1 = [y4_1,y4_2,y4_3,y4_1];
h = fill(X4_1,Y4_1,'c');
axis([x_neg x_pos y_neg y_pos]);%畫出象限圖
end

上面的程式碼區域，關於我註釋掉的程式碼區域，可以不予理會，其中主要用到兩個主要的matlab函式完成的繪圖，solve函式和fill函式，solve函式是用來求解兩條直線方程的，fill函式是用來完成直線函式圍成區域之間的顏色填充的，我使用的是藍色。你可以使用doc solve和doc fill來檢視matlab對於這兩個函式的詳細解釋。另外plot，和scatter函式也是必不可少的，plot用來畫圖，scatter函式我用來描繪具體的點。

你需要結合你的障礙物圖形，將solve函式中求解的兩條直線方程替換掉，注意之兩條直線方程必須要有交點才行！！！

3    障礙物搜尋的演算法實現

現在障礙物的環境已經構建完成，我們需要讓演算法具備搜尋障礙物的能力，我把它寫成了 searchBarrier函式，這個函式的主要功能可以理解成超聲波感測器，會在可見的視野區域內反饋障礙物的點集，程式碼如下，

function [ Bexist,crosspiont,num,other_crosspoint ] = searchBarrier( xnext,ynext,beta1,beta2,r,confine )
%輸入引數：
% xnext,ynext----機器人下一時刻位置
% beta1,beta2----機器人視野範圍大小
% r----機器人視野長度，半徑
% confine----地圖邊界值
% 輸出引數：
% Bexist----當前位置是否檢測到障礙物,0--沒有，1--有
% crosspiont----搜尋區域與障礙物區域的邊界交點座標
%%測試時使用
% quaBarrier----返回改點在第幾象限
% num----該象限第幾個障礙物,若numbarrier == 32代表到達地圖邊界,若numbarrier ==0代表不在障礙物區域
%%
%機器人探測區域
%將圓形區域與所有該座標系的曲線求解，若解在Barrier區域且同時在搜尋區域則，表示探測到障礙物
Bexist = 0;
crosspiont = [];
count = 1;
other_crosspoint = [];
count_other = 1;
quadrant = 0;
quaBarrier = 0;
num = 0;


%判斷點在哪一個象限
if xnext >= 0 && ynext >= 0
    quadrant = 1;
elseif xnext < 0 && ynext > 0
    quadrant = 2;
elseif xnext < 0 && ynext < 0
    quadrant = 3;
else
    quadrant = 4;
end

syms x y
eqn = (x-xnext)^2+(y-ynext)^2 == r^2;
%%
%第一象限所有邊界曲線
if quadrant == 1
    eqn1_1(1) = x-confine == 0; %地圖邊界1
    eqn1_1(2) = y-confine == 0; %地圖邊界2
    eqn1_1(3) = x-2-y == 0; 
    eqn1_1(4) = 0.5-y == 0; 
    eqn1_1(5) = -x+2-y ==0; 
    eqn1_1(6) = y-x-1 == 0; 
    eqn1_1(7) = y-2.5 == 0; 
    eqn1_1(8) = y+x-5 == 0; 
    eqn1_1(9) = y == 0; 
    eqn1_1(10) = x == 0; 
end
%第二象限所有邊界曲線
if quadrant == 2
    eqn2_1(1) = x+confine == 0; %地圖邊界1
    eqn2_1(2) = y-confine == 0; %地圖邊界2
    eqn2_1(3) = x+2.5-y == 0; 
    eqn2_1(4) = -x-1.5-y == 0; 
    eqn2_1(5) = y-x/3-13/6 ==0; 
%     eqn2_1(6) = x+4.5-y == 0; 
    eqn2_1(6) = y-2*x-8.5 == 0; 
    eqn2_1(7) = y+x+0.5 == 0; 
    eqn2_1(8) = y == 0; 
    eqn2_1(9) = x == 0; 
end
%第三象限所有邊界曲線
if quadrant == 3
    eqn3_1(1) = x+confine == 0; %地圖邊界1
    eqn3_1(2) = y+confine == 0; %地圖邊界2
    eqn3_1(3) = x+1 == 0; 
    eqn3_1(4) = x+3.5 == 0; 
    eqn3_1(5) = y+1 ==0; 
    eqn3_1(6) = y+1.5 == 0; 
    eqn3_1(7) = x+1.5 == 0; 
    eqn3_1(8) = y+2 == 0; 
    eqn3_1(9) = x+2.5 == 0; 
    eqn3_1(10) = y+2.5 == 0; 
    eqn3_1(11) = y == 0; 
    eqn3_1(12) = x == 0; 
end
%第四象限所有邊界曲線
if quadrant == 4
    eqn4_1(1) = x-confine == 0; %地圖邊界1
    eqn4_1(2) = y+confine == 0; %地圖邊界2
    eqn4_1(3) = 1.5*x-5-y == 0; 
    eqn4_1(4) = -x-y == 0; 
    eqn4_1(5) = y+0.5 ==0; 
    eqn4_1(6) = y == 0; 
    eqn4_1(7) = x == 0; 
end
%%
%按象限匹配
switch quadrant
    case 1
        %==========================================================================
        n = length(eqn1_1);
        for i = 1:1:n
            [sx,sy] = solve(eqn,eqn1_1(i),x,y,'Real',true);%只求實數解
            if ~isempty(sx)%有交點
                %判斷交點是否在Barrier中
                n1 = length(sx);%確認有幾個交點
                for j = 1:1:n1
                   [numbarrier,quadrantBarrier] = Barrier(sx(j),sy(j),confine);
                   
%                    if sx(j) < 0 || sy(j) < 0 || sx(j) > confine || sy(j) > confine%說明點不在第一象限地圖區域內,那麼結束當前迴圈
%                        continue;
%                    end
                   if sx(j) < -confine || sy(j) < -confine || sx(j) > confine || sy(j) > confine%說明點不在地圖區域內,那麼結束當前迴圈
                       continue;
                   end     
                   
                   if numbarrier ~=0%在障礙物空間中
                        %還得判斷是否在視野範圍中
                        beta = asin((sy(j)-ynext)/sqrt((sx(j)-xnext)^2+(sy(j)-ynext)^2));%sin(beta) = y-ynext/(sqrt(x-xnext)^2+(y-ynext)^2) 得到的是弧度值
                        %因為asin只能得出 -90 <= beta <= 90之間的角度，所以還需要細化判斷
                        if sx(j)-xnext <0 && sy(j)-ynext > 0%說明在第二象限
                            beta = beta+pi/2;
                        end
                        if sx(j)-xnext < 0 && sy(j)-ynext < 0%說明在第三象限
                             beta = beta-pi/2;
                        end
                      %%
                        %當x=0或y=0時，會出現奇異性要單獨討論
                        if sy(j)-ynext ==0
                            if sx(j)-xnext > 0
                                beta = 0;
                            elseif sx(j)-xnext < 0
                                beta = pi;
                            end
                        end
                        if (beta >= beta1 && beta <= beta2) || ((beta-2*pi) >= beta1 && (beta-2*pi) <= beta2) || ( (2*pi+beta) >= beta1 && (2*pi+beta) <= beta2 )%因為一個角度有兩種表達方式，在-270 <= beta <= 270範圍中
                            Bexist = 1;
                            if sx(j) < 0 || sy(j) < 0 || sx(j) > confine || sy(j) > confine%說明點不在第一象限地圖區域內,那麼結束當前迴圈
                                other_crosspoint(:,count_other) = [sx(j);sy(j)];
                                count_other = count_other+1;
                                continue;
                            end
                            crosspiont(:,count) = [sx(j);sy(j)];
                            num(count) = numbarrier;
                            count = count+1;
                            quaBarrier = quadrant; 
                        end
                   end
                end
            end
        end
%===========================================================================
%===========================================================================
    case 2
        n = length(eqn2_1);
        for i = 1:1:n
            [sx,sy] = solve(eqn,eqn2_1(i),x,y,'Real',true);%只求實數解
            if ~isempty(sx)%有交點
                %判斷交點是否在Barrier中
                n1 = length(sx);%確認有幾個交點
                for j = 1:1:n1
                   [numbarrier,quadrantBarrier] = Barrier(sx(j),sy(j),confine);
                   
                   if sx(j) > 0 || sy(j) < 0 || sx(j) < -confine || sy(j) > confine%說明點不在第一象限,那麼結束當前迴圈
                       continue;
                   end
                   
                   if numbarrier ~=0%在障礙物空間中
                        %還得判斷是否在視野範圍中
                        beta = asin((sy(j)-ynext)/sqrt((sx(j)-xnext)^2+(sy(j)-ynext)^2));%sin(beta) = y-ynext/(sqrt(x-xnext)^2+(y-ynext)^2) 得到的是弧度值
                        %因為asin只能得出 -90 <= beta <= 90之間的角度，所以還需要細化判斷
                        if sx(j)-xnext <0 && sy(j)-ynext > 0%說明在第二象限
                            beta = beta+pi/2;
                        end
                        if sx(j)-xnext < 0 && sy(j)-ynext < 0%說明在第三象限
                             beta = beta-pi/2;
                        end
                      %%
                        %當x=0或y=0時，會出現奇異性要單獨討論
                        if sy(j)-ynext ==0
                            if sx(j)-xnext > 0
                                beta = 0;
                            elseif sx(j)-xnext < 0
                                beta = pi;
                            end
                        end
                        if beta >= beta1 && beta <= beta2 || ((beta-2*pi) >= beta1 && (beta-2*pi) <= beta2) || ( (2*pi+beta) >= beta1 && (2*pi+beta) <= beta2 )%因為一個角度有兩種表達方式，在-270 <= beta <= 270範圍中
                            Bexist = 1;
                            crosspiont(:,count) = [sx(j);sy(j)];
                            num(count) = numbarrier;
                            count = count+1;
                            quaBarrier = quadrant;
                        end
                   end
                end
            end
        end

    case 3
        n = length(eqn3_1);
        for i = 1:1:n
            [sx,sy] = solve(eqn,eqn3_1(i),x,y,'Real',true);%只求實數解
            if ~isempty(sx)%有交點
                %判斷交點是否在Barrier中
                n1 = length(sx);%確認有幾個交點
                for j = 1:1:n1
                   [numbarrier,quadrantBarrier] = Barrier(sx(j),sy(j),confine);
                   
                   if sx(j) > 0 || sy(j) > 0 || sx(j) < -confine || sy(j) < -confine%說明點不在第一象限,那麼結束當前迴圈
                       continue;
                   end
                   
                   if numbarrier ~=0%在障礙物空間中
                        %還得判斷是否在視野範圍中
                        beta = asin((sy(j)-ynext)/sqrt((sx(j)-xnext)^2+(sy(j)-ynext)^2));%sin(beta) = y-ynext/(sqrt(x-xnext)^2+(y-ynext)^2) 得到的是弧度值
                        %因為asin只能得出 -90 <= beta <= 90之間的角度，所以還需要細化判斷
                        if sx(j)-xnext < 0 && sy(j)-ynext > 0%說明在第二象限
                            beta = beta+pi/2;
                        end
                        if sx(j)-xnext < 0 && sy(j)-ynext < 0%說明在第三象限
                             beta = beta-pi/2;
                        end
                      %%
                        %當x=0或y=0時，會出現奇異性要單獨討論
                        if sy(j)-ynext ==0
                            if sx(j)-xnext > 0
                                beta = 0;
                            elseif sx(j)-xnext < 0
                                beta = pi;
                            end
                        end
                        
                        if beta >= beta1 && beta <= beta2 || ((beta-2*pi) >= beta1 && (beta-2*pi) <= beta2) || ( (2*pi+beta) >= beta1 && (2*pi+beta) <= beta2 )%因為一個角度有兩種表達方式，在-270 <= beta <= 270範圍中
                            Bexist = 1;
                            crosspiont(:,count) = [sx(j);sy(j)];
                            num(count) = numbarrier;
                            count = count+1;
                            quaBarrier = quadrant;
                        end
                   end
                end
            end
        end

    case 4
         n = length(eqn4_1);
         for i = 1:1:n
            [sx,sy] = solve(eqn,eqn4_1(i),x,y,'Real',true);%只求實數解
            if ~isempty(sx)%有交點
                %判斷交點是否在Barrier中
                n1 = length(sx);%確認有幾個交點
                for j = 1:1:n1
                   [numbarrier,quadrantBarrier] = Barrier(sx(j),sy(j),confine);
                   
                   if sx(j) < 0 || sy(j) > 0 || sx(j) > confine || sy(j) < -confine%說明點不在第四象限,那麼結束當前迴圈
                       continue;
                   end
                   
                   if numbarrier ~=0%在障礙物空間中
                        %還得判斷是否在視野範圍中
                        beta = asin((sy(j)-ynext)/sqrt((sx(j)-xnext)^2+(sy(j)-ynext)^2));%sin(beta) = y-ynext/(sqrt(x-xnext)^2+(y-ynext)^2) 得到的是弧度值
                        %因為asin只能得出 -90 <= beta <= 90之間的角度，所以還需要細化判斷
                        if sx(j)-xnext < 0 && sy(j)-ynext > 0%說明在第二象限
                            beta = beta+pi/2;
                        end
                        if sx(j)-xnext < 0 && sy(j)-ynext < 0%說明在第三象限
                             beta = beta-pi/2;
                        end
                      %%
                        %當x=0或y=0時，會出現奇異性要單獨討論
                        if sy(j)-ynext ==0
                            if sx(j)-xnext > 0
                                beta = 0;
                            elseif sx(j)-xnext < 0
                                beta = pi;
                            end
                        end
                        
                        if ( beta >= beta1 && beta <= beta2 ) || ( (beta-2*pi) >= beta1 && (beta-2*pi) <= beta2 ) || ( (2*pi+beta) >= beta1 && (2*pi+beta) <= beta2 ) %因為一個角度有兩種表達方式，在-270 <= beta <= 270範圍中
                            Bexist = 1;
                            crosspiont(:,count) = [sx(j);sy(j)];
                            num(count) = numbarrier;
                            count = count+1;
                            quaBarrier = quadrant;
                        end
                   end
                end
            end
        end

end



end

 這個函式相對更加複雜一些，然而對於你的障礙物資訊，你只需要關注於每一個quadrant後的eqn1_1，eqn2_1，eqn3_1，eqn4_1這幾個陣列中存放的地圖邊界，虛擬xoy座標系和你的障礙物構成的直線方程即可，其他各種運動過程中的轉角，角度變換等等的邏輯我都在switch-case語句中處理好了，你只需要關注於設計你的障礙物直線方程即可。

注意，隊醫移動機器人的視野範圍beta1,beta2，要始終滿足beta1<= beta2！！！

4    至此你所需要的MATLAB平臺下的障礙物環境已經搭建好了，而且可以搜尋障礙物資訊了

你現在需要讓你的移動機器人在運動的過程中，不斷的預測下一時刻行走的位置是否處於障礙物之中，或者很靠近障礙物，這些位置都是十分危險的位置，很容易發生碰撞，因此，我設計了一個簡單的評估移動機器人行走安全的評價函式EvaSafe，程式碼如下，

function [ IsMysafe ] = EvaSafe( robotPosition,ii,v,dt,seta,aifa,quadrant,confine,safe_level )
%輸入引數：
% robotPosition----機器人位置集合，用來記錄走過的位置，防止重複行走
% robotPosition為2*n矩陣，第一行為x軸位置，第二行為對應的y軸資料
% ii----機器人第幾個位置資料,即robotPosition中的列值
% v----機器人運動速度
% dt----取樣時間
% seta----速度方向與世界座標系夾角 -180 <= seta <= 180
% aifa----機器人視野範圍
% quadrant----第幾象限的agent
% confine----地圖邊界值
% safe_level----機器人路線安全等級，對應預測的安全位置個數---- safe_level = n*v*dt=n*v;
%輸出引數：
% IsMysafe----是否安全,在不跳出之前象限區域限制的前提下。0----safe,1----dangrous

IsMysafe = 0;
numbarrier = 0;
over_quadrant = 0;
% xnext = [];
% ynext = [];
% position = robotPosition(:,ii);
xnext = robotPosition(1,ii);
ynext = robotPosition(2,ii);
% [ xnext,ynext,beta1,beta2 ] = RobotMoving( position,i,v,dt,seta,aifa );
%將無限接近0的資料歸零化
if abs(xnext - 0) < 0.0001 
    xnext = 0;
end

if abs(ynext - 0) < 0.0001 
    ynext = 0;
end

xnext = xnext+safe_level*cos(seta);
ynext = ynext+safe_level*sin(seta);

%將無限接近0的資料歸零化
if abs(xnext - 0) < 0.0001 
    xnext = 0;
end

if abs(ynext - 0) < 0.0001 
    ynext = 0;
end
%%
%================================================================
%判斷預測位置是否在障礙物區域
[numbarrier,quadrantBarrier] = Barrier( xnext,ynext,confine);
%================================================================
%判斷點在哪一個象限
if xnext >= 0 && ynext >= 0
    flag_quadrant = 1;
elseif xnext < 0 && ynext > 0
    flag_quadrant = 2;
elseif xnext < 0 && ynext < 0
    flag_quadrant = 3;
else
    flag_quadrant = 4;
end
%超過象限區域
if flag_quadrant ~= quadrant
      over_quadrant = 1;
end
%==============================================================
%判斷該位置是否走過

if numbarrier ~= 0 || over_quadrant ~= 0
    IsMysafe = 1;
end

end

在函式的註釋中，所有的輸入/輸出引數，解釋的很清楚，這裡就不再贅述了。

關於演算法的具體實現，你可以在這裡下載,

link:https://download.csdn.net/download/simileciwh/10777849

至此你可以，應用自己的演算法到這個障礙物環境中去，驗證自己設計的路徑規劃演算法或者地圖構建演算法的效能和效果了。