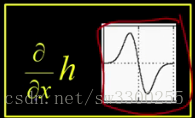
6.邊緣檢測:梯度——梯度計算中濾波器的線性特性的利用_6
到現在為止還挺好。
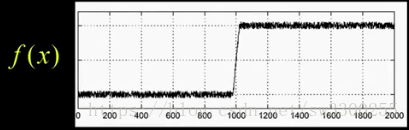
在現實世界中,在這裡有這個小函式f(x):
它有一些東西,然後它需要一個跳躍,它在那裡有更多的東西:
這就是強度作為x的函式。
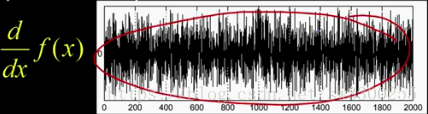
如果我實際上只是通過做一個正確的差異來獲取該函式的梯度。
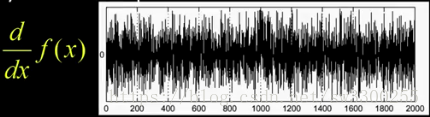
我要做的是,應用導數運算元,得到這個:
有人可能會問,邊緣在哪裡。
我們可以看到,這條邊,哎呀,我漏了,這條邊就在這裡。如圖:
但在這導數這個圖種很混亂,很找到邊緣在哪裡。如圖:
問題當然是我們增加了噪音。
這個噪聲使得我們在各處都有正的和負的導數。
我們來看一下噪聲對一些導數的影響,以及我們可以做些什麼。
這裡我們再次提供了更多的條紋鴨,這裡我們有梯度影象:
你可以看到,當我給影象新增噪音時,我的梯度開始崩潰。
那是我開始看到這個,我有一點點高斯噪音,現在我變成了這些大椒鹽噪音。
感覺像是鹽和胡椒的聲音,只是這些大的尖峰在我的導數中發生。
所以我們必須以某種方式處理這種噪音。
您可能知道如何處理,我們如何處理噪音?
我們過濾,我們要順利擺脫它,我們之前做過。
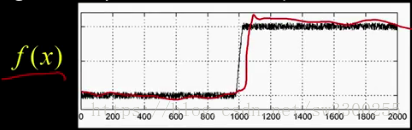
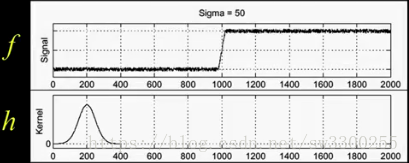
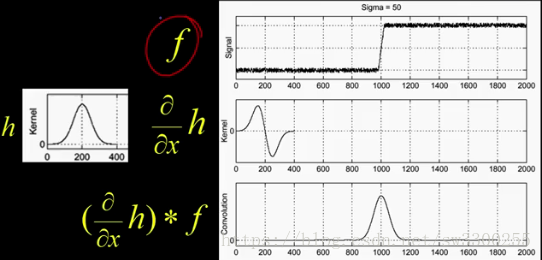
這是我的影象 f,現在讓我應用一個平滑核心,h。如圖:
我只是想平滑一點。所以,當我平滑它的時候,我使用這個是 h 來卷積 f 。
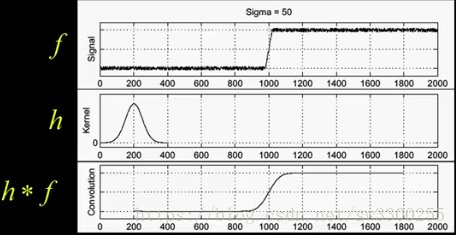
無論你是進行卷積還是相關。H 與 f 卷積,你現在看到我得到了一個漂亮,流暢的函式:
現在,我們已經平滑了訊號,我們可以採取導數,你看到的是,我們得到這個好,平滑的峰值:
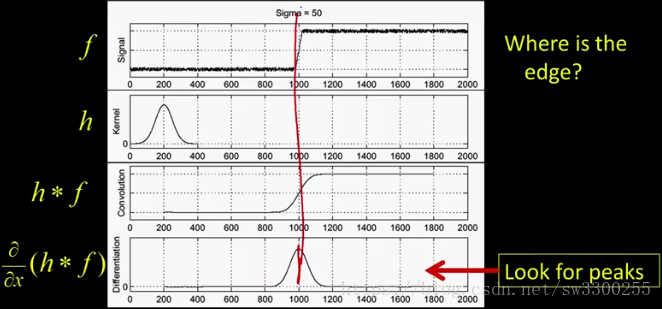
那麼,邊緣在哪裡?
邊緣將在此處達到此峰值,對應於那邊的邊緣。
所以基本上為了找到我們的邊緣,我們將不得不以某種方式基本上應用平滑漸變並尋找一些峰值。
在我們繼續這樣做之前,請記住關聯屬性和線性等的整個概念。
我們可以自己儲存一個操作,因為與f卷積的h的導數與用f卷積的h的導數相同。
那麼當我們進行邊緣檢測時,它會是什麼樣子?
請繼續看以下內容:
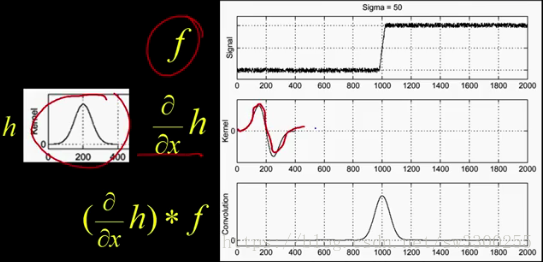
所以在這裡我們擁有與以前相同的 f:
現在,我取h,然後求導,現在看起來像這樣:
當我將該函式直接應用於f時,我得到的值與我上次得到的值相同。Wow,你會發現神奇的地方出現了:
這必須是因為線性運算元的關聯屬性,導數和濾波是這些線性運算元。
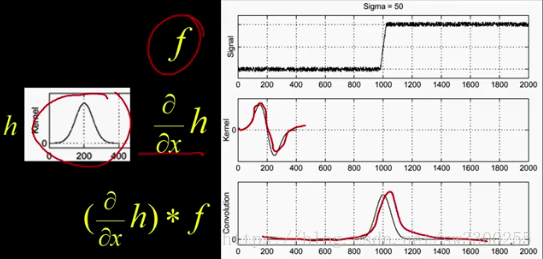
好的,最後一個問題。我們現在有這個美好的峰值:
我們必須找到峰值。我們必須找到該導數的最大值。
我們如何找到最大值?
我們取更多的導數。
所以我們將不得不採取另一種導數。
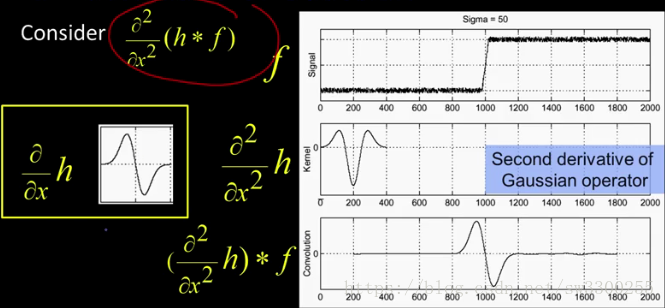
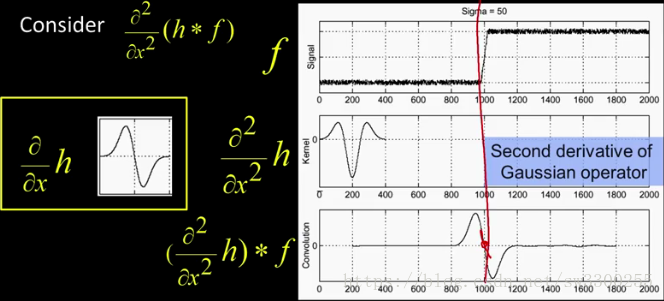
所以現在,我們只需要做一個二階導數,而不是隻做一個導數:
在h是高斯函式之前,這是高斯函式的一階導數。
如果我們再對它求導,就會得到這個,有時被稱為倒墨西哥帽。
你會看到,當我們在2D中做的時候,對吧,因為它有點像這個草帽狀的,但是上下的,對吧?
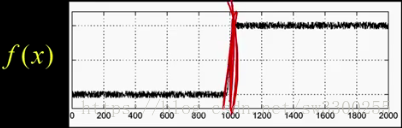
當我們將該運算子應用於影象時,我們可以通過這個強斜率得到這個漂亮的零交叉:
這就是我們的邊:
這是一個強力的斜率零交叉。
我們不需要找到一般的最大值,我們只需要找到任何一個值為0的地方附近有一個強梯度。
小測驗:
那麼我們利用了哪些線性性質首先求核的導數然後應用它,而不需要在前兩個步驟中做?
A、相關;
B、可交換;
C、區分;
D、A 和 C;
答案:D。我們採用了相關,並且區分是線性的,並且可以應用相關,
這就是允許我們採用運算子的導數並將其應用於整個影象的原因。
我們稍後會談一談,為什麼有時這是好事。
但最簡單的解釋是,假設我的影象是1,000 x 1,000。
假設導數是31×31。
我可以把31乘31的導數,這個很小,然後將其應用到我的1,000乘1,000。
或者,我可以把31×31應用到1000×1000上然後對整個1000×1000求導,這比對小一點的濾波器求導的計算量要大得多。
這就是我們這樣做的原因之一。
——學會編寫自己的程式碼,才能練出真功夫。