論文筆記6：Increasing the Action Gap: New Operators for Reinforcement Learning
參考文獻：New Operators for Reinforcement Learning
同名知乎：uuummmmiiii
這篇文章實在是式子多，整個看懵，網上目前沒啥人看過這篇，論文有兩部分，我掙扎了一下看了第一部分，所以第二部分具體作者創新了什麼，做了什麼相關推導我也不知道，哭泣。
如有錯誤還請指出，本人小白，希望幫助更多的人，一同進步。
論文分為兩部分：前部分：作者介紹新提出的新運算元。
後半部分：為這個運算元可以保持最優性推匯出了充分條件。
創新點：提出了最優儲存運算元（optimality-preserving）,稱為consistent Bellman operator
改進：在Q函式更新公式，加入此運算元。公式如下:
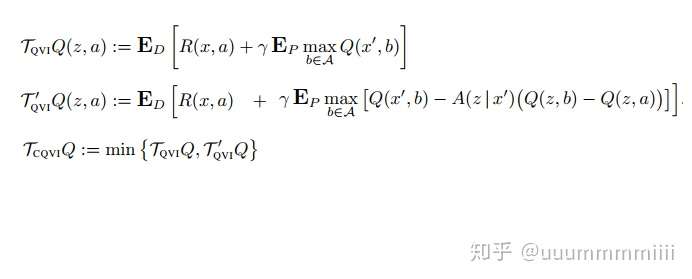
原Q函式更新公式：
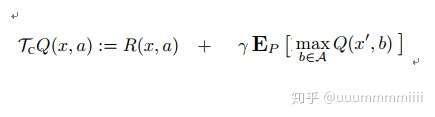
改進原因：Q值發生小擾動會導致錯誤識別最佳動作，原來的Q函式更新方式不穩定（因為Q*的選取是選策略π）
帶來益處：1、可以增加action gap（the value difference between optimal and second best action）,緩解近似和估計誤差對選擇動作（貪婪策略）的影響。
2、可以將這個運算元用於進行對連續狀態的離散化。
3、 可以提升在一些需要運作在很好的time scale下的遊戲（個人理解為
是一種需要即時性戰略的遊戲，並非棋盤類和傳統電子遊戲的那種回合制的遊戲：作者舉出三個例子，視訊遊戲、實時市場、機器人遊戲）
Abstract
本文提出了一種在Q函式中的最優保留運算元，我們成為 the consistent Bellman operator,這裡融合了局部策略一致性的概念。我們說明了，這種區域性一致性可以在每個狀態下增加action gap，這樣可以緩和近似和估計誤差對選擇動作（貪婪策略）的影響。最優運算元也可以應用在對連續狀態的離散化和時間相關的問題，並且在論文中進行了驗證，證明這個運算元可以產生優良效能。
為了擴充套件區域性一致性運算元的概念，我們有推匯出了其可以保持最優性的充分條件，引入包含我們這個consistent Bellman operator的運算元群（家族）。作為推論，我們提供了Baird's advantage learning algorithm 的最優性證明和其他可以使action gap增加的運算元。
最終我們在60 Atari 2600 games 中例項驗證了這些新運算元的強大力量。
The consistent Bellman operator
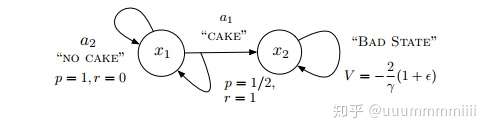
開始利用上面這個吃蛋糕的簡單例子，論證了一大堆複雜式子，就是說明，這個可以給出平穩策略π的Q函式（原），實際上這個Q函式是不平穩的。引出我們對於Q函式式子的改變，加入我們的新運算元。
----------------------------------------------證明分割線------------------------------------
（複雜推導如下，不看可略過）
stationary，平穩性，即與時間無關。
我們假定我們的研究域 是確定性平穩的空間（確定性過程：一類特殊的隨機過程.是不受隨機因素影響的過程；平穩過程是一種重要的隨機過程，其主要的統計特性不會隨時間推移而改變）
在上圖中，我們描述了MDP的兩個狀態，一個有立即獎勵但是是harmful選擇即吃蛋糕狀態 （稱為‘cake’），另一個選擇是沒有立即獎勵即不吃蛋糕狀態
（稱為‘no cake’），我們假設給agent持續的蛋糕供給（γ>0）。
吃蛋糕，既選擇狀態‘cake’，可以發生狀態轉變到x2（稱為‘bad state’），其狀態值函式：
：=-2(1+
)
對於x1狀態，選擇a1動作的動作狀態值函式
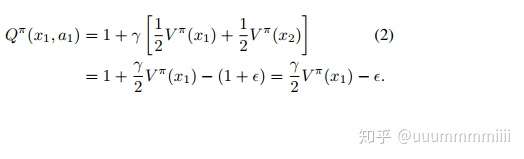
對於x1狀態，選擇a2動作的動作狀態值函式，對於任何策略π，均是不吃蛋糕（選擇動作a2）是最優策略，則V*(x1)=Q*(x1,a2)=0,因為
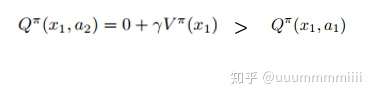
這樣產生了action gap：
則Q*(x1,a1)=- ，對於策略
(x1)=a1的值函式，
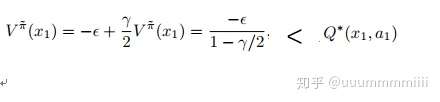
Q*(x1,a1)=- ，一旦吃掉蛋糕（選取動作a1）然後就放棄了（不太懂。。）
-------------------------------------------證明結束------------------------------------------
然後作者推出對Q函式的改進：
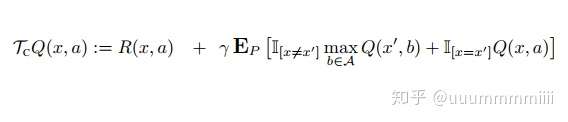改進式(1)
後面進行了證明，分析為什麼這樣新增是最優的保留運算元，並且可以增加gap
Aggregation methods
作者覺著上面對Q函式的改進（改進式1）又有侷限了，一個原因是大部分P(x|s,a)是0或者接近0，另一個原因是在進行檢測
的時候，描述狀態的特徵被排除了一些有意義的部分。
作者利用集結策略（aggregation scheme）對改進式1進行改變：
改進式(2)
其中集結策略是一個元組形式（Z,A,D）,Z是一系列集結狀態，A是從X到Z的一個對映，D是從Z到X的一個對映：
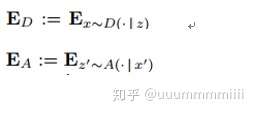
Q-value Interpolation
作者又做了改進，最後得出下面這個
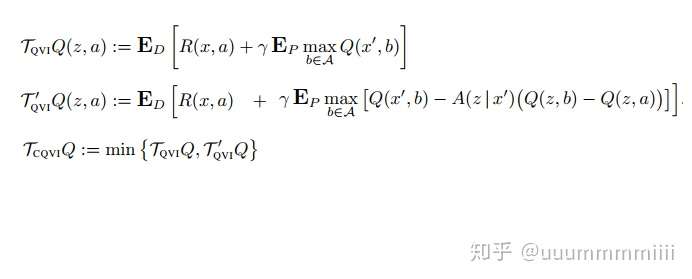改進式(3)
Experiments on the bicycle domain
實驗為了讓agent在平衡模擬自行車的同時還要騎到在初始位置東邊的1km目標處,為觀察運算元產生動作狀態值函式的quality，我們用值迭代演算法而非q-learning演算法去計算Q(s,a)
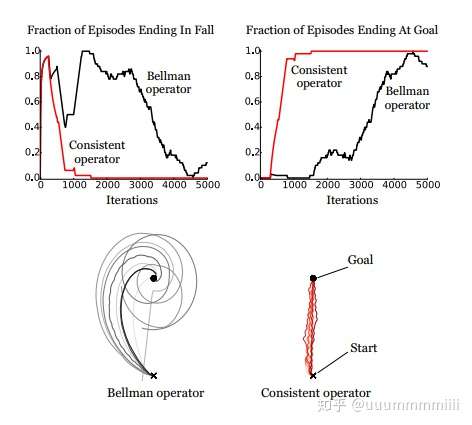
圖中上面兩個圖表示對於在兩種遊戲結束情況（摔倒，到達目標），從價值迭代中產生出的動作狀態值函式隨迭代次數的變化，可以發現，基於consistent operator的動作狀態值函式很快就收斂，但是原來的Bellman operator 收斂慢，到遊戲結束所需時間長。
圖中下面兩個圖表示自行車軌跡，用Bellman operator ，發現一直在goal附近打轉，而consistent operator很快就到達goal。
後面也做了三個運算元的實驗：DQN(用Bellman operator),AL,PAL（這倆具體是啥沒看，就是作者提出的新運算元，就摘要裡說的運算元大家族，沒準還做了一些改變），主要的改變就是在loss值處，用DQN中target網路去計算。發現大部分遊戲比DQN效能好。
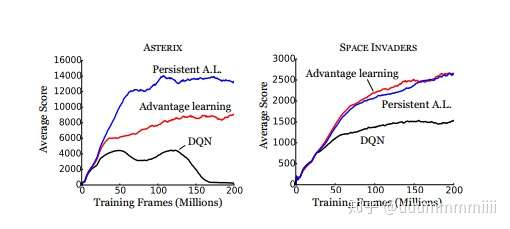
我後面放棄了。。。個人感覺跟相關DQN演算法的改進沒有什麼關係，只是推導充分條件，證明，實驗驗證了，自行選擇，我就碼到這裡，暈死了，不過感覺筆記寫出來的理解的更深了，隨時還可以看一看。