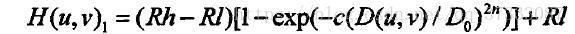影象處理中，對於影象增強有多種技術，主要分為空域增強技術以及頻域增強技術。空域增強中，對於細節的強化有拉普拉斯銳化，對於整體影象的有直方圖歸一化，gamma變換，log變換等。而在頻域增強中，以同態濾波為主。

    對於一幅影象，以輪廓為代表的細節主要集中在高頻部分，因此，對於影象的增強，對於影象效果的強化主要是以增強高頻為主。同態濾波就是這麼一種濾波器，它的思想基於一副原圖可以把它看做是入射分量以及反射分量的結合。即f(x,y)=i(x,y)*r(x,y),其中f(x,y)為原影象，i(x,y)為入射分量，r(x,y)為反射分量。入射分量因光照強度的一致性屬於低頻部分，光在經過物體表面反射時，即反射分量，反射分量可看做是物體自身的線性變換，屬於高頻部分，應該在影象處理中進行增強。那麼我們目的就很明確了，找出一個頻率濾波器，能夠對高頻進行增強，同時能夠對低頻進行相對抑制。傳統的同態濾波有高斯同態濾波

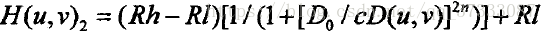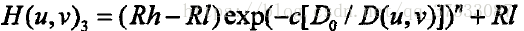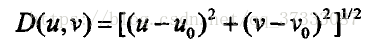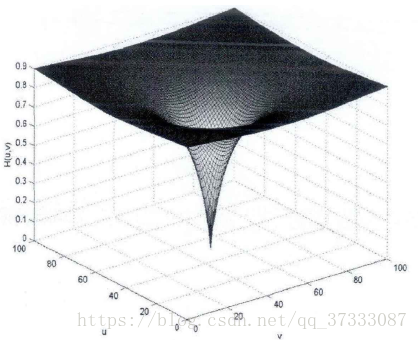
，巴特沃斯同態濾波器，指數型同態濾波器。式中，Rh、Rl分別為高頻和低頻增益，D0為截止頻率，c是控制斜面銳化的常數，這三種同態濾波器都需要3種以上引數來進行控制，因此提出了一種改進型的同態濾波，僅需單個引數就能達到理想的效果，該傳遞函式為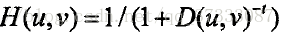，該函式的三維圖如下，傳遞函式的取值在[0,0.9],引數t是唯一一個控制引數

下面為同態濾波的主要流程

接著獻上基於opencv的原始碼

#include <iostream>
#include <opencv2/opencv.hpp>
using namespace std;
using namespace cv;
int t = 1;
Mat src;


void homomorphic(int, void* userdata)
{

double t2 = (double)(t-10) / 110;
vector<Mat> rgb_split;
cv::split(src, rgb_split);
Mat dst;
for (int i = 0; i < 3; i++)
{
Mat original = rgb_split[i].clone();
Mat frame_log,padded,fourier_src,spatial,reinforce_src;
original.convertTo(frame_log, CV_32FC1);
frame_log += 1;
log(frame_log, frame_log);
//將圖片從空域中轉至頻域
int m = frame_log.rows;
int n = frame_log.cols;
copyMakeBorder(frame_log, padded, 0, m - frame_log.rows, 0, n - frame_log.cols, BORDER_CONSTANT, Scalar::all(0));
Mat image_planes[] = { Mat_<float>(padded), Mat::zeros(padded.size(), CV_32F) };
cv::merge(image_planes, 2, fourier_src);
dft(fourier_src, fourier_src);


//構造同態濾波器
Mat hu(fourier_src.size(), CV_32FC1, Scalar::all(0));
Point center = Point(hu.rows / 2, hu.cols / 2);
for (int i = 0; i < hu.rows; i++)
{
float* data = hu.ptr<float>(i);
for (int j = 0; j < hu.cols; j++)
data[j] = (double)1 / (1 + pow(sqrt(pow(center.x - i, 2) + pow((center.y - j), 2)), -t2));
}
Mat butterworth_channels[] = { Mat_<float>(hu), Mat::zeros(hu.size(), CV_32F) };
cv::merge(butterworth_channels, 2, hu);


//進行頻域卷積操作，得到強化過後的頻域圖，將其轉回空域
cv::mulSpectrums(fourier_src, hu, fourier_src, 0);
cv::idft(fourier_src, spatial, DFT_SCALE);

//對影象進行還原
cv::exp(spatial, spatial);
vector<Mat> planes;
cv::split(spatial, planes);
cv::magnitude(planes[0], planes[1], reinforce_src);
/*Mat temp;
normalize(reinforce_src, temp, 0, 255, NORM_MINMAX);
temp.convertTo(temp, CV_8UC1);*/
//這裡採用偏差法對影象進行還原，類似的也可以用直方圖歸一化，只不過我試過直方圖歸一化效果不是很好
Mat mean_val, stddev_value;
cv::meanStdDev(reinforce_src, mean_val, stddev_value);
double min, max, minmax;
min = mean_val.at<double>(0, 0) - 2 * stddev_value.at<double>(0, 0);
max = mean_val.at<double>(0, 0) + 2 * stddev_value.at<double>(0, 0);
minmax = max - min;
for (int i = 0; i < planes[0].rows; i++)
for (int j = 0; j < planes[0].cols; j++)
reinforce_src.at<float>(i, j) = 255 * (reinforce_src.at<float>(i, j) - min) / minmax;
reinforce_src.convertTo(reinforce_src, CV_8UC1);
rgb_split[i] = reinforce_src.clone();

}
cv::merge(rgb_split, dst);
//下面對影象進行飽和度拉伸以及灰度線性變換以獲得更加生動的圖片
cvtColor(dst, dst, COLOR_BGR2HSV);
vector<Mat> hsv;
split(dst, hsv);
for (int i = 0; i < hsv[1].rows; i++)
for (int j = 0; j < hsv[1].cols; j++)
hsv[1].at<uchar>(i, j) = hsv[1].at<uchar>(i, j) * 4 / 3;
for (int i = 0; i < hsv[1].rows; i++)
for (int j = 0; j < hsv[1].cols; j++)
{
if (hsv[2].at<uchar>(i, j) < 235)
hsv[2].at<uchar>(i, j) = hsv[2].at<uchar>(i, j) * 45 /50-40;
/*else if (hsv[2].at<uchar>(i, j)>220)
hsv[2].at<uchar>(i, j) = (hsv[2].at<uchar>(i, j) - 151) * 55 / 180 + 200;*/
}
merge(hsv, dst);
cvtColor(dst, dst, COLOR_HSV2BGR);
imshow("效果圖", dst);


}
Mat Fourier_Transform(Mat input)
{
Mat result;


return result;
}
int main(int argc, char** argv[])
{
src = imread("aaa.jpg");
imshow("原圖", src);

createTrackbar("t", "原圖", &t, 100, homomorphic);
waitKey(0);
return 0;
}

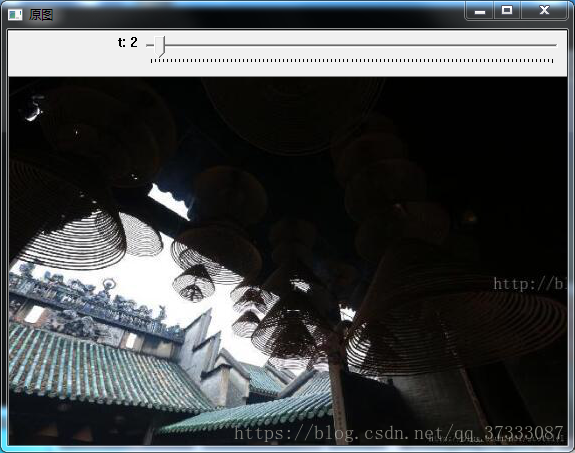
下面是原圖

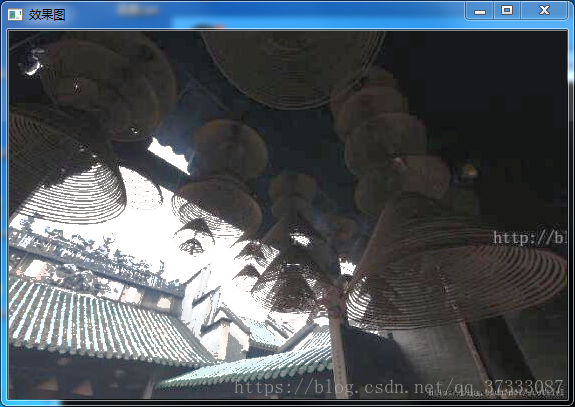
緊接的是效果圖