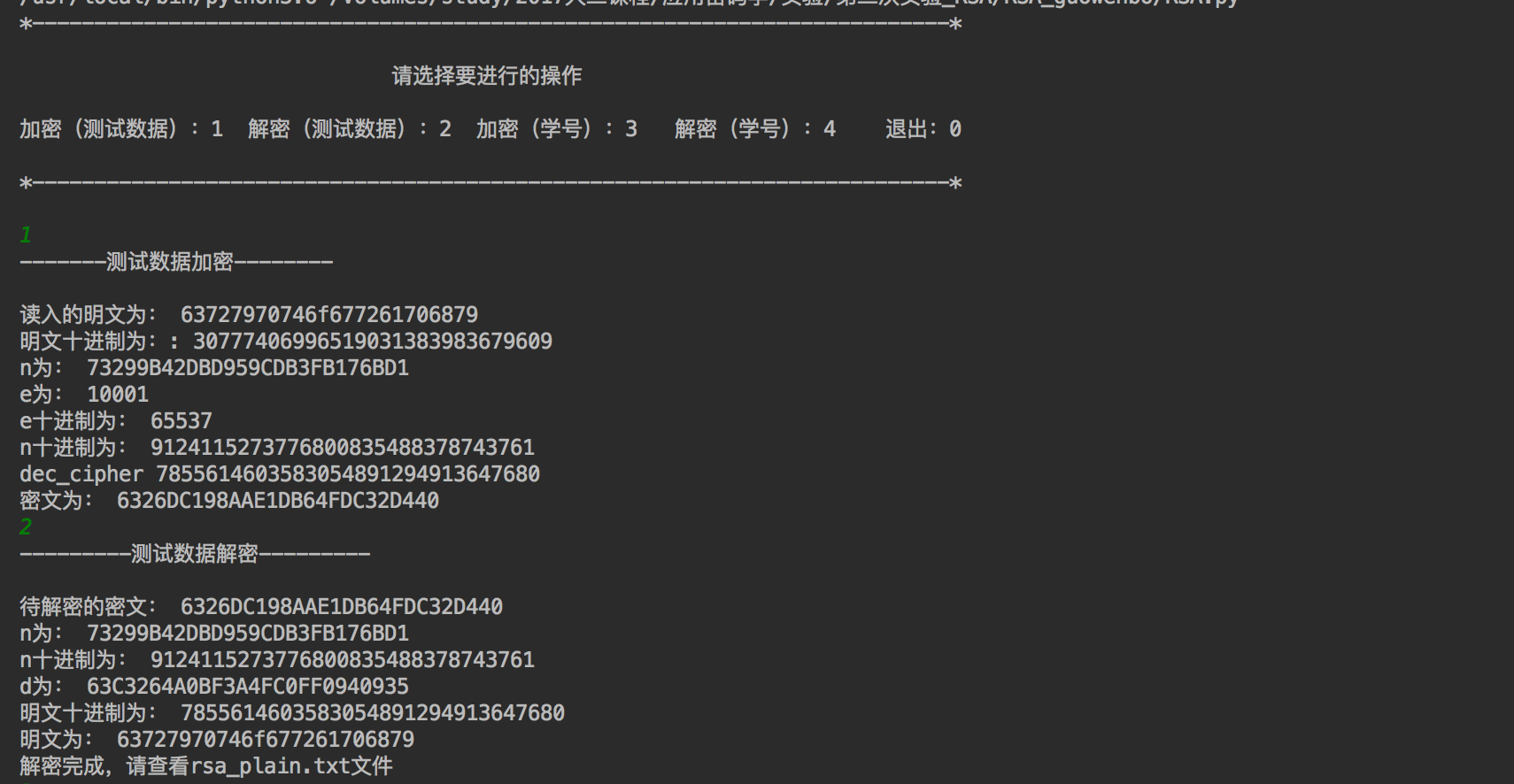
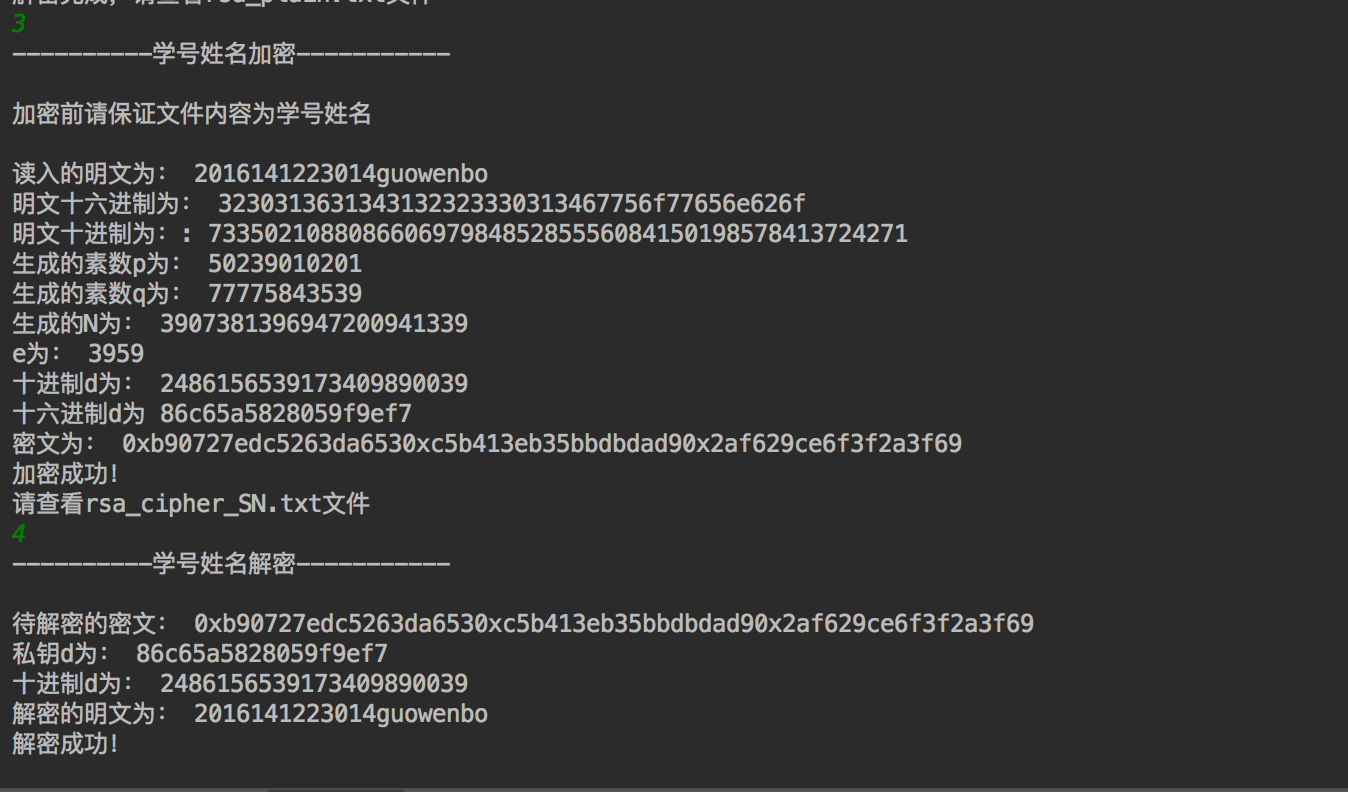
#-*- coding：UTF-8 -*-


'''


    time:  2018-5-30


    content:RSA

    python 3.6

    mac os

'''

from random import randint
import random
import math
import sys


def  charToAscii(message):       #將字元轉化為ASCII碼
  Output = []
  for i in message:
      Output.append(ord(i))
  return Output

                                  #將ASCII碼變為十六進位制
def AsciiToHex(message):
  Output = ''
  for each in message:
    Output = Output + str(hex(each)).split('x')[1]
  return Output


def Hex_to_dec(hexnumber):        #16進位制字串轉化為十進位制
    decnumber = int(hexnumber,16)
    return decnumber



def dec_to_Hex(decumber):          #十進位制轉化為十六進位制
    hexnumber = hex(decumber)
    return hexnumber



def big_P_Q():                  #產生兩個大素數
    flag = 0
    while not flag:
        p = random.randrange(10**10,10**11)

        if charge_sushu_1(p) and _ack(2,p):

            q = random.randrange(p,10**11)
            if charge_sushu_1(q) and p != q and _ack(2,q):
                flag = 1
    return p,q







def fastExpMod(b, e, m):          #快速求模
    result = 1
    while e != 0:
        if (e&1) == 1:
            # ei = 1, then mul
            result = (result * b) % m
        e >>= 1
        # b, b^2, b^4, b^8, ... , b^(2^n)
        b = (b*b) % m
    return result

def gcd(a,b):                     #判斷互素
    if a<b:
        a,b = b,a
    while b != 0:
        temp = a%b
        a = b
        b = temp
    return (a,b)


def find_e(En):                     #尋找e
    while 1:
        e = random.randrange(10000)
        if gcd(e,En) == (1,0):
            break

    return e

def find_d(e,s):                    #求d

    u1, u2, u3 = 1, 0, e
    v1, v2, v3 = 0, 1, s
    while v3 != 0:
        q = u3 // v3
        v1, v2, v3, u1, u2, u3 = (u1 - q * v1), (u2 - q * v2), (u3 - q * v3), v1, v2, v3
    return u1 % s

# def miller_Rabin(n):                #素性檢驗
#     if n == 1:
#         return False
#     if n == 2:
#         return True
#     N = n-1
#     a = randint(2, N)
#     t = int(math.floor(math.log(N,2)))
#     u = 1
#     while t>0:
#         u = N/2**t
#         if N%2*t==0 and u%2 == 1:
#             break
#         u = t-1
#     b = fastExpMod(a,u,n)
#     if(b == 1):
#         return True
#
#     for n in range(0,t,1):
#         if(b == n-1):
#             return True
#         else:
#             b = fastExpMod(b,2,n)
#     return False

def charge_sushu_1(n):
    Sushu = (2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41
                 , 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97)
    for y in Sushu:
        if n % y == 0:
            return False
    return True

def _ack(a,n):

    a1 = pow(17-a,n,n)
    a2 = pow(17,n,n) - (a%n)
    if a1 == a2:
        return 1
    else:
        return 0

def charge_sushu_2(n, k):
    if n < 2:
           return False
    d = n - 1
    r = 0
    while not (d & 1):
            r += 1
            d >>= 1
    for i in range(k):
            a = randint(120)        #隨機數
            x = fastExpMod(a, d, n)
            if x == 1 or x == n - 1:
                    continue
            for i in range(r - 1):
                    x = fastExpMod(x, 2, n)
            if x == 1:
                    return False
            if x == n - 1:
                    break
    else:
            return False
    return True


以上是函式的主要函式
 

輸出結果:

原始碼檢視此地址:https://download.csdn.net/download/weixin_39641975/10458941