【題目描述】
如果一個字串包含兩個相鄰的重複子串，則稱它是“容易的串”，其他串稱為“困難的串”。例如， BB、ABCDABCD都是容易的串，而D、DC、ABDAD、CBABCBA都是困難的串。

輸入正整數n和L，輸出由前L個字元組成的、字典序第k個困難的串。例如，當L=3時，前7個困難的串 分別為A、AB、ABA、ABAC、ABACA、ABACAB、ABACABA。輸入保證答案不超過80個字元。

樣例輸入：
7 3
30 3

樣例輸出：
ABACABA
ABACABCACBABCABACABCACBACABA

【整體思路】
想要求第n小的困難的串，我首先想到的方法是生成-測試法，也就是依次生成並判斷生成的是否是“困難的串”：這需要依次檢查所有長度為偶數的子串，並判斷前一半是否等於後一半。
這樣做的後果是會產生很多不必要的計算，比如下面的串：
ABCABC

其實回想前面學到的八皇后問題，它們的判斷思想是一脈相承的。對八皇后問題來說，使用二維陣列 vis[3][] 來儲存上一層放置的狀態，我們不用判斷所有前面（n-1）層的，因為不符合要求的放置沒有後續的遞迴操作，只有符合要求的部分才會執行DFS(cur+1)。

【判斷部分】
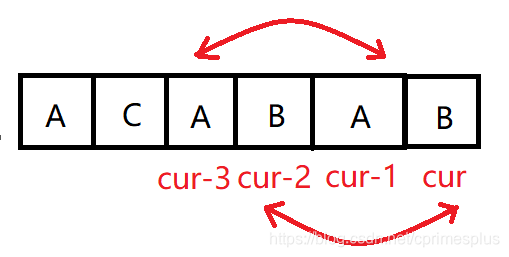
因為不需要考慮所有的子串（不合格的已經被篩掉了），因此只需要考慮不同長度的字尾串是否相同。判斷原理如下圖：
先判斷後綴長度為1的：

再判斷後綴長度為2的：

以此類推，直到 j*2>=len+1 為止。
不難發現，比較的位置是從每次從尾端開始，因為比較的距離為i，所以作比較的元素應該是a[cur]和a[cur-i]，又因為需要從a[cur]比較到a[cur-i]，因此應該加上一層迴圈來控制移動的次數。

【程式碼】

//困難的串
#include<iostream>
#include<string>
#include<cmath>
#include<cstring>
#include<ctype.h>
using namespace std;
const int maxn = 10000 + 10;
int cnt = 0, n, L, a[maxn];
bool check(int cur, int j)	//j為列舉的倍數
{
	for (int i = 0;i < j;i++)
		if (a[cur - i] != a[cur - j - i]) return true;
	return false;
}
int DFS(int cur)	//cur個元素
{
	if (cnt++ == n)
	{
		for (int i = 0;i < cur;i++) cout << (char)(a[i] + 'A');cout << endl;
		return 0;
	}
	for (int i = 0;i < L;i++)
	{
		int ok = 1;
		a[cur] = i;
		for (int j = 1;j * 2 <= cur + 1;j++)	//j為列舉的倍數
			if (!check(cur, j)) //只要前後完全相同就非法
			{
				ok = 0;break;
			}
		if (ok)	//如果不非法就繼續遞迴
			if (!DFS(cur + 1)) return 0;
	}
	return 1;
}
int main()
{
	cin >> n >> L;
	memset(a, 0, sizeof(a));
	DFS(0);
	return 0;
}