Java後端面試題(演算法)
1、寫⼀個字串反轉函式。
方法一:(利用遞迴實現)
public static String reverse1(String s) {
int length = s.length();
if (length <= 1)
return s;
String left = s.substring(0, length / 2);
String right = s.substring(length / 2, length);
return reverse1(right) + reverse1(left); //呼叫遞迴
}方法二:(拼接字串)
public static String reverse2(String s) { int length = s.length(); String reverse = ""; for (int i = 0; i < length; i++) reverse = s.charAt(i) + reverse; return reverse; }
方法三:(利用陣列,倒序輸出)
public static String reverse3(String s) {
char[] array = s.toCharArray();
String reverse = "";
for (int i = array.length - 1; i >= 0; i--)
reverse += array[i];
return reverse;
}方法四:(利用StringBuffer的內建reverse方法)
public static String reverse4(String s) { return new StringBuffer(s).reverse().toString(); }
方法五:(利用臨時變數,交換兩頭數值)
public static String reverse5(String orig) {
char[] s = orig.toCharArray();
int n = s.length - 1;
int halfLength = n / 2;
for (int i = 0; i <= halfLength; i++) {
char temp = s[i];
s[i] = s[n - i];
s[n - i] = temp;
}
return new String(s);
}方法六:(利用位異或操作,交換兩頭資料)
public static String reverse6(String s) {
char[] str = s.toCharArray();
int begin = 0;
int end = s.length() - 1;
while (begin < end) {
str[begin] = (char) (str[begin] ^ str[end]);
str[end] = (char) (str[begin] ^ str[end]);
str[begin] = (char) (str[end] ^ str[begin]);
begin++;
end--;
}
return new String(str);
}方法七:(利用棧結構)
public static String reverse7(String s) {
char[] str = s.toCharArray();
Stack<Character> stack = new Stack<Character>();
for (int i = 0; i < str.length; i++)
stack.push(str[i]);
String reversed = "";
for (int i = 0; i < str.length; i++)
reversed += stack.pop();
return reversed;
}2、氣泡排序,氣泡排序的優化⽅案。
原理:比較兩個相鄰的元素,將值大的元素交換至右端。
思路:設陣列的長度為N:
- 比較前後相鄰的二個數據,如果前面資料大於後面的資料,就將這二個數據交換。
- 這樣對陣列的第0個數據到N-1個數據進行一次遍歷後,最大的一個數據就“沉”到陣列第N-1個位置。
- N=N-1,如果N不為0就重複前面二步,否則排序完成。
/**
* 氣泡排序的第一種實現, 沒有任何優化
* @param a
* @param n
*/
public static void bubbleSort1(int [] a, int n){
int i, j;
for(i=0; i<n; i++){//表示n次排序過程。
for(j=1; j<n-i; j++){
if(a[j-1] > a[j]){//前面的數字大於後面的數字就交換
//交換a[j-1]和a[j]
int temp;
temp = a[j-1];
a[j-1] = a[j];
a[j]=temp;
}
}
}
}
測試程式碼:
public static void main(String[] args) {
int[] arr = {1,1,2,0,9,3,12,7,8,3,4,65,22};
BubbleSort.bubbleSort1(arr, arr.length);
for(int i:arr){
System.out.print(i+",");
}
}執行結果:
0,1,1,2,3,3,4,7,8,9,12,22,65,
優化一:如果對於一個本身有序的序列,或則序列後面一大部分都是有序的序列,上面的演算法就會浪費很多的時間開銷,這裡設定一個標誌flag,如果這一趟發生了交換,則為true,否則為false。明顯如果有一趟沒有發生交換,說明排序已經完成。
/**
* 設定一個標誌,如果這一趟發生了交換,則為true,否則為false。明顯如果有一趟沒有發生交換,說明排序已經完成。
* @param a
* @param n
*/
public static void bubbleSort2(int [] a, int n){
int j, k = n;
boolean flag = true;//發生了交換就為true, 沒發生就為false,第一次判斷時必須標誌位true。
while (flag){
flag=false;//每次開始排序前,都設定flag為未排序過
for(j=1; j<k; j++){
if(a[j-1] > a[j]){//前面的數字大於後面的數字就交換
//交換a[j-1]和a[j]
int temp;
temp = a[j-1];
a[j-1] = a[j];
a[j]=temp;
//表示交換過資料;
flag = true;
}
}
k--;//減小一次排序的尾邊界
}
}執行測試main函式結果:
0,1,1,2,3,3,4,7,8,9,12,22,65,
優化二:比如,現在有一個包含1000個數的陣列,僅前面100個無序,後面900個都已排好序且都大於前面100個數字,那麼在第一趟遍歷後,最後發生交換的位置必定小於100,且這個位置之後的資料必定已經有序了,也就是這個位置以後的資料不需要再排序了,於是記錄下這位置,第二次只要從陣列頭部遍歷到這個位置就可以了。如果是對於上面的氣泡排序演算法2來說,雖然也只排序100次,但是前面的100次排序每次都要對後面的900個數據進行比較,而對於現在的排序演算法3,只需要有一次比較後面的900個數據,之後就會設定尾邊界,保證後面的900個數據不再被排序。
public static void bubbleSort3(int [] a, int n){
int j , k;
int flag = n ;//flag來記錄最後交換的位置,也就是排序的尾邊界
while (flag > 0){//排序未結束標誌
k = flag; //k 來記錄遍歷的尾邊界
flag = 0;
for(j=1; j<k; j++){
if(a[j-1] > a[j]){//前面的數字大於後面的數字就交換
//交換a[j-1]和a[j]
int temp;
temp = a[j-1];
a[j-1] = a[j];
a[j]=temp;
//表示交換過資料;
flag = j;//記錄最新的尾邊界.
}
}
}
}執行測試例子結果:
0,1,1,2,3,3,4,7,8,9,12,22,65,
時間複雜度:
若記錄序列的初始狀態為"正序",則氣泡排序過程只需進行一趟排序,在排序過程中只需進行n-1次比較,且不移動記錄;反之,若記錄序列的初始狀態為"逆序",則需進行n(n-1)/2次比較和記錄移動。因此氣泡排序總的時間複雜度為O(n*n)。
3.快速排序。 快排的最優時間複雜度,最差複雜度。
快排的基本思想: 通過選擇的參考值將待排序記錄分割成獨立的兩部分,一部分全小於選取的參考值,另一部分全大於選取的參考值。對分割之後的部分再進行同樣的操作直到無法再進行該操作位置(可以使用遞迴)。
選擇陣列的第一個元素為參考值。
import java.util.Arrays;
public class QuickSort {
public static void main(String[] args) {
int[] num = { 1, 3, 4, 8, 5, 10, 22, 15, 16 };
QuickSort.quickSort(num, 0, num.length - 1);
System.out.println(Arrays.toString(num));
}
public static void quickSort(int[] a, int start, int end) {
// 該值定義了從哪個位置開始分割陣列
int ref;
if (start < end) {
// 呼叫partition方法對陣列進行排序
ref = partition(a, start, end);
// 對分割之後的兩個陣列繼續進行排序
quickSort(a, start, ref - 1);
quickSort(a, ref + 1, end);
}
}
/**
* 選定參考值對給定陣列進行一趟快速排序
*
* @param a 陣列
* @param start (切分)每個陣列的第一個的元素的位置
* @param end (切分)每個陣列的最後一個的元素位置
* @return 下一次要切割陣列的位置
*/
public static int partition(int[] a, int start, int end) {
// 取陣列的第一個值作為參考值(關鍵資料)
int refvalue = a[start];
// 從陣列的右邊開始往左遍歷,直到找到小於參考值的元素
while (start < end) {
while (end > start && a[end] >= refvalue) {
end--;
}
// 將元素直接賦予給左邊第一個元素,即pivotkey所在的位置
a[start] = a[end];
// 從序列的左邊邊開始往右遍歷,直到找到大於基準值的元素
while (end > start && a[start] <= refvalue) {
start++;
}
a[end] = a[start];
return end;
}
// 最後的start是基準值所在的位置
a[start] = refvalue;
return start;
}
}時間複雜度分析:
- 在最優的情況下,Partition每次都劃分得很均勻,快速排序演算法的時間複雜度為O(nlogn)。
- 最糟糕情況下的快排,當待排序的序列為正序或逆序排列時,時間複雜度為O(n^2)。
空間複雜度分析:
- 最好情況,遞迴樹的深度為log2n,其空間複雜度也就為O(logn)
- 最壞情況,需要進行n‐1遞迴呼叫,其空間複雜度為O(n),平均情況,空間複雜度也為O(logn)。
一種簡單優化的方式:
三向切分快速排序 :核心思想就是將待排序的資料分為三部分,左邊都小於比較值,右邊都大於比較值,中間的數和比較值相等.三向切分快速排序的特性就是遇到和比較值相同時,不進行資料交換, 這樣對於有大量重複資料的排序時,三向切分快速排序演算法就會優於普通快速排序演算法,但由於它整體判斷程式碼比普通快速排序多一點,所以對於常見的大量非重複資料,它並不能比普通快速排序多大多的優勢 。
4、歸併排序
兩路歸併排序演算法思路
分而治之(divide - conquer);每個遞迴過程涉及三個步驟
第一, 分解: 把待排序的 n 個元素的序列分解成兩個子序列, 每個子序列包括 n/2 個元素.
第二, 治理: 對每個子序列分別呼叫歸併排序MergeSort, 進行遞迴操作
第三, 合併: 合併兩個排好序的子序列,生成排序結果.

演算法實現
此演算法的實現不像圖示那樣簡單,現分三步來討論。首先從巨集觀上分析,首先讓子表表長 L=1 進行處理;不斷地使 L=2*L ,進行子表處理,直到 L>=n 為止,把這一過程寫成一個主體框架函式 mergesort 。然後對於某確定的子表表長 L ,將 n 個記錄分成若干組子表,兩兩歸併,這裡顯然要迴圈若干次,把這一步寫成一個函式 mergepass ,可由 mergesort 呼叫。最後再看每一組(一對)子表的歸併,其原理是相同的,只是子表表長不同,換句話說,是子表的首記錄號與尾記錄號不同,把這個歸併操作作為核心演算法寫成函式 merge ,由 mergepass 來呼叫。假設我們有一個沒有排好序的序列,那麼首先我們使用分割的辦法將這個序列分割成一個一個已經排好序的子序列,然後再利用歸併的方法將一個個的子序列合併成排序好的序列。分割和歸併的過程可以看下面的圖例。

程式碼實現:
public static int[] sort(int[] a,int low,int high){
int mid = (low+high)/2;
if(low<high){
sort(a,low,mid);
sort(a,mid+1,high);
//左右歸併
merge(a,low,mid,high);
}
return a;
}
public static void merge(int[] a, int low, int mid, int high) {
int[] temp = new int[high-low+1];
int i= low;
int j = mid+1;
int k=0;
// 把較小的數先移到新陣列中
while(i<=mid && j<=high){
if(a[i]<a[j]){
temp[k++] = a[i++];
}else{
temp[k++] = a[j++];
}
}
// 把左邊剩餘的數移入陣列
while(i<=mid){
temp[k++] = a[i++];
}
// 把右邊邊剩餘的數移入陣列
while(j<=high){
temp[k++] = a[j++];
}
// 把新陣列中的數覆蓋nums陣列
for(int x=0;x<temp.length;x++){
a[x+low] = temp[x];
}
}演算法分析:
(1)穩定性
歸併排序是一種穩定的排序。
(2)儲存結構要求
可用順序儲存結構。也易於在連結串列上實現。
(3)時間複雜度
對長度為n的檔案,需進行趟二路歸併,每趟歸併的時間為O(n),故其時間複雜度無論是在最好情況下還是在最壞情況下均是O(nlgn)。
(4)空間複雜度
需要一個輔助向量來暫存兩有序子檔案歸併的結果,故其輔助空間複雜度為O(n),顯然它不是就地排序。
注意:
若用單鏈表做儲存結構,很容易給出就地的歸併排序
5、單向連結串列,查詢中間的那個元素。
設定兩個指標,一個快指標,每次走兩步,一個慢指標,每次走一步。
public class searchMid {
public Node method(Node head) {
Node p=head;
Node q=head;
while(q!=null&&q.next!=null&&q.next.next!=null) {
p=p.next;
q=q.next.next;
}
return p;
}
}
6、⼆分查詢的時間複雜度,優勢。
二分查詢又稱折半查詢,它是一種效率較高的查詢方法。
折半查詢的演算法思想是將數列按有序化(遞增或遞減)排列,查詢過程中採用跳躍式方式查詢,即先以有序數列的中點位置為比較物件,如果要找的元素值小 於該中點元素,則將待查序列縮小為左半部分,否則為右半部分。通過一次比較,將查詢區間縮小一半。 折半查詢是一種高效的查詢方法。它可以明顯減少比較次數,提高查詢效率。但是,折半查詢的先決條件是查詢表中的資料元素必須有序。
折半查詢法的優點是比較次數少,查詢速度快,平均效能好;其缺點是要求待查表為有序表,且插入刪除困難。因此,折半查詢方法適用於不經常變動而查詢頻繁的有序列表。
二分演算法步驟描述
① 首先確定整個查詢區間的中間位置 mid = ( left + right )/ 2
② 用待查關鍵字值與中間位置的關鍵字值進行比較;
若相等,則查詢成功
若大於,則在後(右)半個區域繼續進行折半查詢
若小於,則在前(左)半個區域繼續進行折半查詢
③ 對確定的縮小區域再按折半公式,重複上述步驟。
最後,得到結果:要麼查詢成功, 要麼查詢失敗。折半查詢的儲存結構採用一維陣列存放。 折半查詢演算法舉例
對給定數列(有序){ 3,5,11,17,21,23,28,30,32,50,64,78,81,95,101},按折半查詢演算法,查詢關鍵字值為81的資料元素。
二分查詢演算法討論:
優點:ASL≤log2n,即每經過一次比較,查詢範圍就縮小一半。經log2n 次計較就可以完成查詢過程。
缺點:因要求有序,所以要求查詢數列必須有序,而對所有資料元素按大小排序是非常費時的操作。另外,順序儲存結構的插入、刪除操作不便利。
考慮:能否通過一次比較拋棄更多的部分(即經過一次比較,使查詢範圍縮得更小),以達到提高效率的目的。……?
可以考慮把兩種方法(順序查詢和折半查詢)結合起來,即取順序查詢簡單和折半查詢高效之所長,來達到提高效率的目的?實際上這就是分塊查詢的演算法思想。
public class BinarySearch {
/**
* 二分查詢演算法
*
* @param srcArray 有序陣列
* @param key 查詢元素
* @return key的陣列下標,沒找到返回-1
*/
public static void main(String[] args) {
int srcArray[] = {3,5,11,17,21,23,28,30,32,50,64,78,81,95,101};
System.out.println(binSearch(srcArray, 0, srcArray.length - 1, 81));
}
// 二分查詢遞迴實現
public static int binSearch(int srcArray[], int start, int end, int key) {
int mid = (end - start) / 2 + start;
if (srcArray[mid] == key) {
return mid;
}
if (start >= end) {
return -1;
} else if (key > srcArray[mid]) {
return binSearch(srcArray, mid + 1, end, key);
} else if (key < srcArray[mid]) {
return binSearch(srcArray, start, mid - 1, key);
}
return -1;
}
// 二分查詢普通迴圈實現
public static int binSearch(int srcArray[], int key) {
int mid = srcArray.length / 2;
if (key == srcArray[mid]) {
return mid;
}
int start = 0;
int end = srcArray.length - 1;
while (start <= end) {
mid = (end - start) / 2 + start;
if (key < srcArray[mid]) {
end = mid - 1;
} else if (key > srcArray[mid]) {
start = mid + 1;
} else {
return mid;
}
}
return -1;
}
}7、⼀個單向連結串列,刪除倒數第N個數據。
public ListNode removeNthFromEnd(ListNode head, int n)
{
//求出連結串列長度
int len = 0;//連結串列長度
ListNode p,q;
p = head;
while(p!=null)
{
len++;
p = p.next;
}
if(n>len)
return null;
p = head;
q = head;
for(int i = 0;i<len-n;i++)
{
p = q;
q = q.next;
}
//當刪除的是第一個節點的時候
if(p==q)
head = p.next;
if(q!=null)
{
p.next = q.next;
q.next = null;
}
return head;
}8、遍歷二叉樹
public class BinaryTree {
int data; //根節點資料
BinaryTree left; //左子樹
BinaryTree right; //右子樹
public BinaryTree(int data) //例項化二叉樹類
{
this.data = data;
left = null;
right = null;
}
public void insert(BinaryTree root,int data){ //向二叉樹中插入子節點
if(data>root.data) //二叉樹的左節點都比根節點小
{
if(root.right==null){
root.right = new BinaryTree(data);
}else{
this.insert(root.right, data);
}
}else{ //二叉樹的右節點都比根節點大
if(root.left==null){
root.left = new BinaryTree(data);
}else{
this.insert(root.left, data);
}
}
}
}當建立好二叉樹類後可以建立二叉樹例項,並實現二叉樹的先根遍歷,中根遍歷,後根遍歷,程式碼如下:
public class BinaryTreePreorder {
public static void preOrder(BinaryTree root){ //先根遍歷
if(root!=null){
System.out.print(root.data+"-");
preOrder(root.left);
preOrder(root.right);
}
}
public static void inOrder(BinaryTree root){ //中根遍歷
if(root!=null){
inOrder(root.left);
System.out.print(root.data+"--");
inOrder(root.right);
}
}
public static void postOrder(BinaryTree root){ //後根遍歷
if(root!=null){
postOrder(root.left);
postOrder(root.right);
System.out.print(root.data+"---");
}
}
public static void main(String[] str){
int[] array = {12,76,35,22,16,48,90,46,9,40};
BinaryTree root = new BinaryTree(array[0]); //建立二叉樹
for(int i=1;i<array.length;i++){
root.insert(root, array[i]); //向二叉樹中插入資料
}
System.out.println("先根遍歷:");
preOrder(root);
System.out.println();
System.out.println("中根遍歷:");
inOrder(root);
System.out.println();
System.out.println("後根遍歷:");
postOrder(root);
}建立好的二叉樹圖形如下:
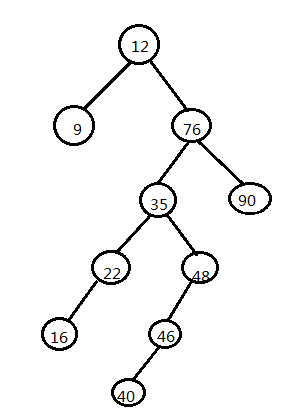
當執行上面的程式後結果如下:
先根遍歷:
12-9-76-35-22-16-48-46-40-90-
中根遍歷:
9--12--16--22--35--40--46--48--76--90--
後根遍歷:
9---16---22---40---46---48---35---90---76---12---
