距離度量公式有：歐幾里得距離，明可夫斯基距離，曼哈頓距離，切比雪夫距離，馬氏距離等；相似度的度量公式有：餘弦相似度，皮爾森相關係數，Jaccard相似係數。 補充：歐幾里得距離度量會受特徵不同單位刻度的影響，所以一般需要先進行標準化處理。

pearson

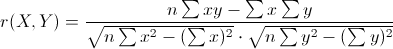
當兩個變數的方差都不為零時，相關係數才有意義，相關係數的取值範圍為[-1,1]

當相關係數為1時，成為完全正相關；當相關係數為-1時，成為完全負相關；相關係數的絕對值越大，相關性越強；相關係數越接近於0，相關度越弱。

皮爾遜相關的約束條件:

1 兩個變數間有線性關係 
2 變數是連續變數 
3 變數均符合正態分佈,且二元分佈也符合正態分佈 
4 兩變數獨立 
在實踐統計中,一般只輸出兩個係數,一個是相關係數,也就是計算出來的相關係數大小,在-1到1之間;另一個是獨立樣本檢驗係數,用來檢驗樣本一致性.

適用範圍

適用於A的評價普遍高於B的評價

歐幾里得距離(Euclidean Distance)

歐氏距離

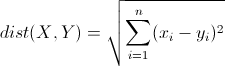
注意事項：

a.因為計算是基於各維度特徵的絕對數值，所以歐氏度量需要保證各維度指標在相同的刻度級別，比如對身高（cm）和體重（kg）兩個單位不同的指標使用歐式距離可能使結果失效。

b.歐幾里得距離是資料上的直觀體現，看似簡單，但在處理一些受主觀影響很大的評分資料時，效果則不太明顯；比如，U1對Item1,Item2 分別給出了2分，4分的評價;U2 則給出了4分，8分的評分。通過分數可以大概看出，兩位使用者褒Item2 ,貶Item1，也許是性格問題，U1 打分更保守點，評分偏低，U2則更粗放一點，分值略高。在邏輯上，是可以給出兩使用者興趣相似度很高的結論。如果此時用歐式距離來處理，得到的結果卻不盡如人意。即評價者的評價相對於平均水平偏離很大的時候歐幾里德距離不能很好的揭示出真實的相似度。

明可夫斯基距離(Minkowski Distance)

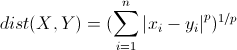
這裡的p值是一個變數，當p=2的時候就得到了上面的歐氏距離

切比雪夫距離(Chebyshev Distance)

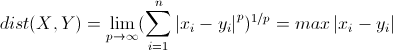
餘弦相似度

餘弦距離使用兩個向量夾角的餘弦值作為衡量兩個個體間差異的大小。相比歐氏距離，餘弦距離更加註重兩個向量在方向上的差異

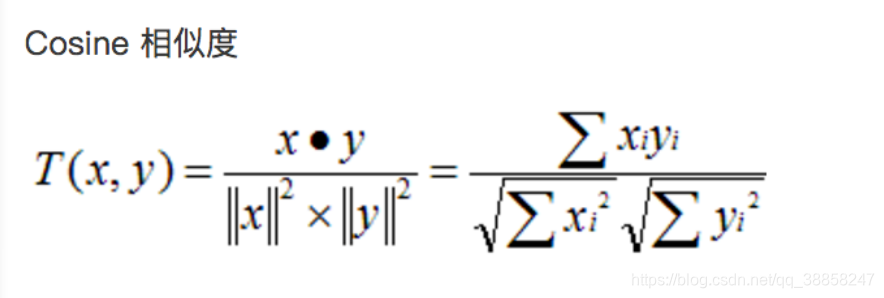
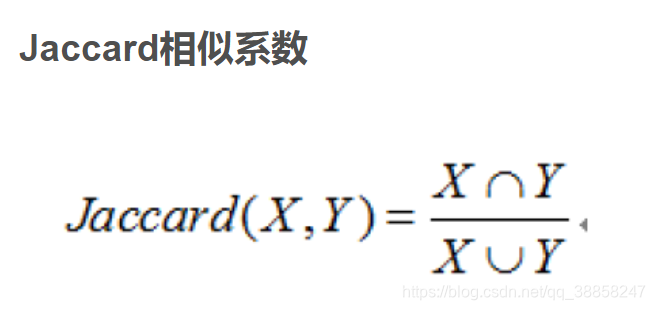
應用場景：比較文字相似度，用於文字查重與去重；計算物件間距離，用於資料聚類等。