1135 Is It A Red-Black Tree （30 分）

There is a kind of balanced binary search tree named red-black tree in the data structure. It has the following 5 properties:

• (1) Every node is either red or black.
• (2) The root is black.
• (3) Every leaf (NULL) is black.
• (4) If a node is red, then both its children are black.
• (5) For each node, all simple paths from the node to descendant leaves contain the same number of black nodes.

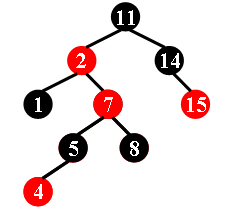
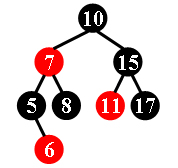
For example, the tree in Figure 1 is a red-black tree, while the ones in Figure 2 and 3 are not.

Figure 1	Figure 2	Figure 3

For each given binary search tree, you are supposed to tell if it is a legal red-black tree.

Input Specification:

Each input file contains several test cases. The first line gives a positive integer K (≤30) which is the total number of cases. For each case, the first line gives a positive integer N (≤30), the total number of nodes in the binary tree. The second line gives the preorder traversal sequence of the tree. While all the keys in a tree are positive integers, we use negative signs to represent red nodes. All the numbers in a line are separated by a space. The sample input cases correspond to the trees shown in Figure 1, 2 and 3.

Output Specification:

For each test case, print in a line "Yes" if the given tree is a red-black tree, or "No" if not.

Sample Input:

3
9
7 -2 1 5 -4 -11 8 14 -15
9
11 -2 1 -7 5 -4 8 14 -15
8
10 -7 5 -6 8 15 -11 17

Sample Output:

Yes
No
No

1.首先知道紅黑樹是二叉搜尋樹，所以我們可以根據先序和中序建樹

判斷是紅黑樹的條件就是1.根節點要是黑色的， 2 不允許有相鄰的紅色節點  3. 左右子樹的黑色節點個數要相同滿足條件輸出yes