2018年江西理工大學C語言競賽初級組第一、二套題解
比賽時發現好多人喜歡多輸出些東西,這反而會答案錯誤。
題目說輸出什麼就輸出什麼,不要多輸出任意東西就行。
第一套:
A 整數序列中兩個相鄰的數,如果後面的數小於前面的數,則稱這兩個數值構成了一個逆序對。例如,整數序列10,4,16,8,21,18,9中包含了4個逆序對。從鍵盤上輸入n(n≤1000)個由空格分隔的整數,程式設計輸出其中包含的逆序對的數量。
簽到題。
1 #include <stdio.h> 2 const int N = 1010; 3 int a[N]; 4 int main() { 5 int n, ans = 0; 6 scanf("%d", &n); 7 for(int i = 1; i <= n; i ++) scanf("%d",&a[i]); 8 for(int i = 1; i < n; i ++) if(a[i] > a[i+1]) ans++; 9 printf("%d\n",ans); 10 return 0; 11 }
B 最近小S不高興了,所以她就想畫圈圈,有大有小的。而現在她想讓你也畫圈圈了^_^。
大小為3的圈圈是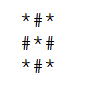 ,大小為4的圈圈是
,大小為4的圈圈是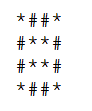 ,大小為5的圈圈是
,大小為5的圈圈是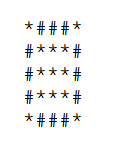 ,依次類推。
,依次類推。
接著送分題
1 #include <stdio.h> 2 3 int main() { 4 int n; 5 scanf("%d", &n); 6 for(int i = 1; i <= n; i ++) { 7 for(int j = 1; j <= n; j ++) { 8 if((i == 1 || i == n) && (j == 1 || j == n)) printf("*"); 9 elseif(i == 1 || i == n || j == 1 || j == n) printf("#"); 10 else printf("*"); 11 } 12 printf("\n"); 13 } 14 return 0; 15 }
C 小明現在有x元,現在想買一件y(y ≤ x)元的物品,商店裡有五種貨幣,100元、20元、10元、5元、1元無限張,服務員會以最小的數量找零錢。問小明用x元買了一件y元的物品後找了多少張零錢。
第一套和第二套都有這題,不過第一套的是沒有50元,第二套的是沒有100元。
貪心,每次找最大的貨幣,這樣就能使的零錢數量最少。
1 #include <stdio.h> 2 3 int main() { 4 int x, y, ans = 0; 5 scanf("%d%d", &x, &y); 6 x -= y; 7 ans += x/100; x %= 100; 8 ans += x/20; x %= 20; 9 ans += x/10; x %= 10; 10 ans += x/5; x %= 5; 11 ans += x/1; 12 printf("%d\n",ans); 13 return 0; 14 }
D 現在的程式設計越來越多了,比如C、C++、Java、Python、C#、PHP等等。現在給定n種程式語言,每種語言還會給一個[1,n]之間的隨機值,保證不重複。現在讓你按隨機值從小到大排序,然後輸出對應的語言。
輸入:
第一行輸入一個整數n(1≤ n ≤ 20)
接下來n行,每行有一個字串和一個隨機值,字串表示一種語言,長度不超過20.隨機值範圍為[1,n]
用結構體儲存程式語言的名字和隨機值。
n最大才20,隨便用種排序就能過。
1 #include <stdio.h> 2 struct Nod{ 3 char s[22]; 4 int id; 5 }e[22], tmp; 6 7 int main() { 8 int n; 9 scanf("%d",&n); 10 for(int i = 1; i <= n; i ++) { 11 scanf("%s%d",e[i].s,&e[i].id); 12 } 13 for(int i = 1; i <= n; i ++) { 14 for(int j = i+1; j <= n; j ++) { 15 if(e[i].id > e[j].id) { 16 tmp = e[i]; 17 e[i] = e[j]; 18 e[j] = tmp; 19 } 20 } 21 } 22 for(int i = 1; i <= n; i ++) printf("%s\n",e[i].s); 23 return 0; 24 }
E 有一個四邊形,現在需要求它的面積。
需要注意的是有凸凹邊形。
將四邊形分成兩個三角形,計算兩個三角形面積的和就是答案。
但由於用凹邊形,將四邊形分成兩個三角形時,有兩種答案。在紙上畫下這兩個分法。其實不難得出面積最小的那個就是四邊形的正確面積。
1 #include <stdio.h> 2 #include <math.h> 3 4 double min(double x, double y) { return x>y?y:x;} 5 double x[4], y[4]; 6 7 double dist(double x1, double y1, double x2, double y2) { 8 return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2)); 9 } 10 double getArea(double a, double b, double c) { 11 double p = (a+b+c)/2.0; 12 return sqrt(p*(p-a)*(p-b)*(p-c)); 13 } 14 int main() { 15 for(int i = 0; i < 4; i ++) scanf("%lf%lf",&x[i], &y[i]); 16 double l1, l2, l3, l4, l5, l6; 17 l1 = dist(x[0],y[0],x[1],y[1]); 18 l2 = dist(x[1],y[1],x[2],y[2]); 19 l3 = dist(x[2],y[2],x[3],y[3]); 20 l4 = dist(x[3],y[3],x[0],y[0]); 21 l5 = dist(x[0],y[0],x[2],y[2]); 22 l6 = dist(x[1],y[1],x[3],y[3]); 23 double area1 = getArea(l1,l2,l5)+getArea(l3,l4,l5); 24 double area2 = getArea(l1,l4,l6)+getArea(l2,l3,l6); 25 printf("%.3lf\n",min(area1,area2)); 26 return 0; 27 }
F 給定一個區間[l, r],從l至r之間的所有數依次轉換成16進位制然後連在一起,接著再轉換成10進位制,最後再對15取模。
將區間內的數字拼接成16進位制,其實16中的每一位都可以轉化成a*16^b的其實。而16^b % 15 == 1 。這樣就是對區間內的數求和在對15取模。
以樣例為例,703710 = 10*16^4+11*10^3+12*16^2+13*16^1+14*10^0。16^4%15==1 10^3%15==1 10^2%15==1 10^1%15==1 10^0%15==1
所以答案就是(10+11+12+13+14)%15 == 0
1 #include <stdio.h> 2 3 int main() { 4 int l, r, ans = 0; 5 scanf("%d%d",&l,&r); 6 for(int i = l; i <= r; i ++) { 7 ans = (ans+i)%15; 8 } 9 printf("%d\n",ans); 10 return 0; 11 }
上面的複雜度高了。 由於%15 所以每16個數就一個迴圈。(1+14)%15=0 (2+13)%15=0...(7+8)%15=0,這樣那些迴圈的都是0,只要計算那些沒有迴圈的就行了。這樣迴圈最多才15次。
1 #include <stdio.h> 2 3 int main() { 4 int l, r, ans = 0; 5 scanf("%d%d", &l, &r); 6 r = r-(r-l)/15*15; 7 for(int i = l; i <= r; i ++) { 8 ans = (ans+i)%15; 9 } 10 printf("%d\n",ans); 11 return 0; 12 }
第二套
A 和第一套一樣。
B 又一道簽到題。判斷下位置就行了。
1 #include <stdio.h> 2 3 char s[4][16]; 4 5 int main() { 6 char ch; 7 for(int i = 0; i < 4; i ++) scanf("%s",s[i]); 8 for(int i = 0; i < 3; i ++) { 9 for(int j = 0; s[i][j]; j ++) { 10 if(s[i][j] == s[3][0]) { 11 printf("%d %d\n",i+1,j+1); 12 } 13 } 14 } 15 return 0; 16 }
C 和第一套的C題解題思路一樣。
1 #include <stdio.h> 2 3 int main() { 4 int x, y, ans = 0; 5 scanf("%d%d", &x, &y); 6 x -= y; 7 ans += x/50; x %= 50; 8 ans += x/20; x %= 20; 9 ans += x/10; x %= 10; 10 ans += x/5; x %= 5; 11 ans += x/1; 12 printf("%d\n",ans); 13 return 0; 14 }
D 數獨是源自18世紀瑞士的一種數學遊戲。是一種運用紙、筆進行演算的邏輯遊戲。玩家需要根據9×9盤面上的已知數字,推理出所有剩餘空格的數字,並滿足每一行、每一列、每一個粗線宮(3×3)內的數字均含1-9,不重複。當然,肯定不會讓你用程式完成沒填好的數獨的。現在給你一個9×9填滿了數的格子,想讓你檢查一下是不是符合數獨的定義。比如下圖是符合數獨的定義的。
判斷下每9列,每9行和每9個粗線是否是1-9都出現了一次就行。
1 #include <stdio.h> 2 #include <string.h> 3 char s[10][10]; 4 bool vis[10]; 5 bool ok1(int x, int y) { 6 memset(vis, 0, sizeof(vis)); 7 for(int i = x; i < x+3; i ++) { 8 for(int j = y; j < y+3; j ++) { 9 if(vis[s[i][j]-'0']) return false; 10 vis[s[i][j]-'0'] = 1; 11 } 12 } 13 return true; 14 } 15 bool ok2(int pos, int flag) { 16 memset(vis, 0, sizeof(vis)); 17 if(flag == 1) { 18 for(int i = 1; i <= 9; i ++) { 19 if(vis[s[pos][i]-'0']) return false; 20 vis[s[pos][i]-'0'] = 1; 21 } 22 } else { 23 for(int i = 1; i <= 9; i ++) { 24 if(vis[s[i][pos]-'0']) return false; 25 vis[s[i][pos]-'0'] = 1; 26 } 27 } 28 return true; 29 } 30 int main() { 31 bool flag = true; 32 for(int i = 1; i <= 9; i ++) scanf("%s",s[i]+1); 33 for(int i = 1; i <= 9; i ++) { 34 if(!ok2(i,1) || !ok2(i,0)) flag = false; 35 } 36 for(int i = 1; i <= 7; i += 3) { 37 for(int j = 1; j <= 7; j += 3) { 38 if(!ok1(i,j)) flag = false; 39 } 40 } 41 if(flag) printf("YES\n"); 42 else printf("NO\n"); 43 return 0; 44 }
E 現在有n個棒棒糖,對於每個棒棒糖都有兩個數Ai,Bi,Ai表示棒棒糖的體積,Bi表示棒棒糖放入水中每秒融化的體積。然後有m個裝滿水的杯子,每個杯子有且僅能放一個棒棒糖,放完一個棒棒糖後就不能再放其它棒棒糖了,在第0s時就應該將選擇的棒棒糖全放在杯子裡。問怎麼選擇棒棒糖使的第s秒到第t秒中間(包括s和t)融化的棒棒糖體積之和最大。
先計算每根棒棒糖在[s,t]間能融化的棒棒糖體積,按從大到小排下序,去前min(n,m)個體積最大的和就是答案了。
1 #include <stdio.h> 2 #define ll long long 3 4 ll res[1010]; 5 int min(int x, int y) {return x>y?y:x;} 6 int max(int x, int y) {return x>y?x:y;} 7 int main() { 8 int n, m, s, t, a, b; 9 scanf("%d%d%d%d",&n, &m, &s, &t); 10 for(int i = 1; i <= n; i ++) { 11 scanf("%d%d", &a, &b); 12 res[i] = min((t-s+1)*b, max(0,a-(s-1)*b)); 13 } 14 for(int i = 1; i <= n; i ++) { 15 for(int j = i+1; j <= n; j ++) { 16 if(res[i] < res[j]) { 17 int tmp = res[i]; 18 res[i] = res[j]; 19 res[j] = tmp; 20 } 21 } 22 } 23 ll ans = 0; 24 for(int i = 1; i <= min(n,m); i ++) ans += res[i]; 25 printf("%lld\n",ans); 26 return 0; 27 }
F 給定兩個整數a和b(保證所有資料不包含前導0),現在你可交換a裡面任意兩個數字,得到一個新的a,使得a為小於等於b的最大整數,例如給定a:1234,b:5555,得到4321。如果找不到小於等於b的最大a,則輸出-1。(輸出也必須保證不包含前導0,例如0123是不合法輸出)。
一開始就將a組成最小的數。然後兩次迴圈,讓兩兩之間的數都交換下位置,看否還是小於等於b,如果是的話就留下來,不是的話就換回來。因為一開始就是最小的數(即前面的≤後面的),所以每次交換成功後都會使得數字變大些。
最後看a是否還是≤b 是的話就輸出答案,否則輸出-1.
1 #include <algorithm> 2 #include <iostream> 3 #include <string.h> 4 #include <stdio.h> 5 #define ll long long 6 using namespace std; 7 char s[20]; 8 ll solve() { 9 ll ans = 0; 10 for(int i = 0; s[i]; i ++) ans = ans*10+s[i]-'0'; 11 return ans; 12 } 13 14 int main() { 15 ll a, b; 16 scanf("%s%lld", &s, &b); 17 int len = strlen(s); 18 sort(s,s+len); 19 for(int i = 0; i < len; i ++) { 20 for(int j = i+1; j < len; j ++) { 21 swap(s[i], s[j]); 22 if(solve() > b) swap(s[i], s[j]); 23 } 24 } 25 a = solve(); 26 if(a <= b) printf("%lld\n",solve()); 27 else printf("-1\n"); 28 return 0; 29 }
