Codeforces Round #247(Div. 2) C. k-Tree DP
Quite recently a creative student Lesha had a lecture on trees. After the lecture Lesha was inspired and came up with the tree of his own which he called a k-tree.
A k-tree is an infinite rooted tree where:
- each vertex has exactly k children;
- each edge has some weight;
- if we look at the edges that goes from some vertex to its children (exactly k edges), then their weights will equal 1, 2, 3, ..., k.
The picture below shows a part of a 3-tree.
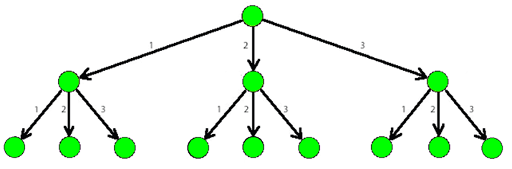
Help Dima find an answer to his question. As the number of ways can be rather large, print it modulo
A single line contains three space-separated integers: n, k and d (1 ≤ n, k ≤ 100; 1 ≤ d ≤ k).
OutputPrint a single integer — the answer to the problem modulo 1000000007 (109 + 7).
Examples input3 3 2output
3input
3 3 3output
1input
4 3 2output
6input
4 5 2output
7
題意:
給定一個k叉樹,且是無限有根樹,每個節點有k個孩子,從左向右依次編號為1,2,3,...k,每條邊有權值,節點連向i號孩子的邊的權值為i,問:從根節點開始向下走,有多少條路徑滿足要求:該路徑權值為n,且路徑上至少有一條邊的權值大於等於d。
題解:
直接求不好求,比較複雜,不過我們可以求出來所以權值為n的路徑,然後再減去不符合要求的路徑:該路徑上所有的邊的權值都小於d。
用dp做。
dp[i]:權值為i的路徑的條數。
dp2[i]:權值為i的,且路徑上的權值都小於d的路徑條數。
答案為:dp[n]-dp2[n]
/****************
*PID:431c div2
*Auth:Jonariguez
*****************
dp[i]:權值為i的路徑的條數
dp2[i]:權值為i,且路徑上的權值都小於d的路徑條數
答案:dp[n]-dp2[n]
*/
#define lson k*2,l,m
#define rson k*2+1,m+1,r
#define rep(i,s,e) for(i=(s);i<=(e);i++)
#define For(j,s,e) For(j=(s);j<(e);j++)
#define sc(x) scanf("%d",&x)
#define In(x) scanf("%I64d",&x)
#define pf(x) printf("%d",x)
#define pfn(x) printf("%d\n",(x))
#define Pf(x) printf("%I64d",(x))
#define Pfn(x) printf("%I64d\n",(x))
#define Pc printf(" ")
#define PY puts("YES")
#define PN puts("NO")
#include <stdio.h>
#include <string.h>
#include <string>
#include <math.h>
#include <set>
#include <map>
#include <stack>
#include <queue>
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
typedef int Ll;
Ll quick_pow(Ll a,Ll b,Ll MOD){a%=MOD;Ll res=1;while(b){if(b&1)res=(res*a)%MOD;b/=2;a=(a*a)%MOD;}return res;}
const int maxn=100+10;
const LL MOD=1e9+7;
LL dp[maxn],dp2[maxn];
int main()
{
int i,j,n,k,d;
while(scanf("%d%d%d",&n,&k,&d)!=EOF){
memset(dp,0,sizeof(dp));
memset(dp2,0,sizeof(dp2));
dp[0]=1;
for(i=1;i<=n;i++){
for(j=1;j<=k;j++){
if(i-j>=0){
dp[i]+=dp[i-j];
dp[i]%=MOD;
}
}
}
dp2[0]=1;
for(i=1;i<=n;i++){
for(j=1;j<d;j++){
if(i-j>=0){
dp2[i]+=dp2[i-j];
dp2[i]%=MOD;
}
}
}
LL res=(dp[n]-dp2[n])%MOD;
if(res<0) res+=MOD;
printf("%I64d\n",res);
}
return 0;
}