Manacher(馬拉車)學習筆記
Manacher可以有效的在\(O(n)\)時間內解決一個字串的迴文子串的題目
目錄
- 簡介
- 講解
- 推介
- 簡單的練習
- 恐怖的練習QAQ
- 小結
簡介
開頭都說了,Manacher是目前解決迴文子串的最有效的方法之一,可以在\(O(n)\)時間內處理出以這個點為中心的最大回文子串長度。
講解
1. 將偶數的迴文子串處理成奇數迴文子串
在暴力處理迴文子串的過程中,我們會把偶數與奇數的分成兩個判斷
相信大家一定會有這個疑問,那麼,我們在開頭、結尾與兩兩字元中間插入一個沒有出現過的字元,如:'#',舉個栗子:aaaa做完處理為:#a#a#a#a#。
那麼偶數的迴文子串就是以'#'為中心的字串。
為什麼在開頭與結尾插入一個'#',首先,仔細思考:
在#a#a#a#a#不管以哪個字元為中心,列舉到的迴文子串的開頭與結尾都肯定是'#'號,如:a#a,我們可以在兩個a再向外擴充套件一個'#'。
如果不在開頭與結尾加的話,就會出現開頭結尾不是'#'的異類迴文子串,如a#a。
那麼,我們就可以愉快直接算長度為奇數的迴文子串了。
2. 統計答案
由於後面的內容會十分的血腥,所以我還是先把簡單的搬到前面。
首先,我們定義一個數組ma陣列,\(ma_{i}\)代表以\(i\)到以\(i\)為中心的最大回文子串的開頭的長度,如:#a#b#b#c#b#,中以\(c\)為中心,組成的最大回文子串為#b#c#b#,c到最右邊的#的串長度為4,所以他的\(ma\)
那麼,如何統計答案?
如圖:
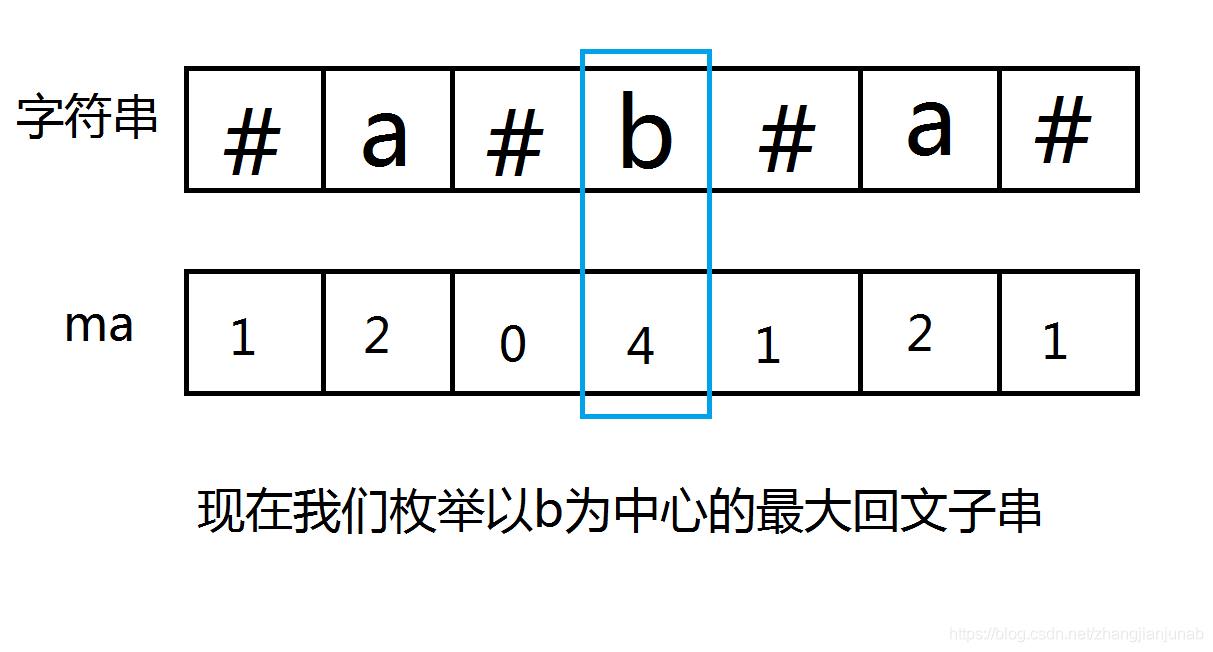
迴歸正題,我們發現,b的ma值是4,同時真正的迴文子串是3(去掉#號),難道就是ma值減1?
沒錯,就是,為什麼?
我們繼續思考:把右邊的字母與左邊的'#'號調轉一下
如圖:
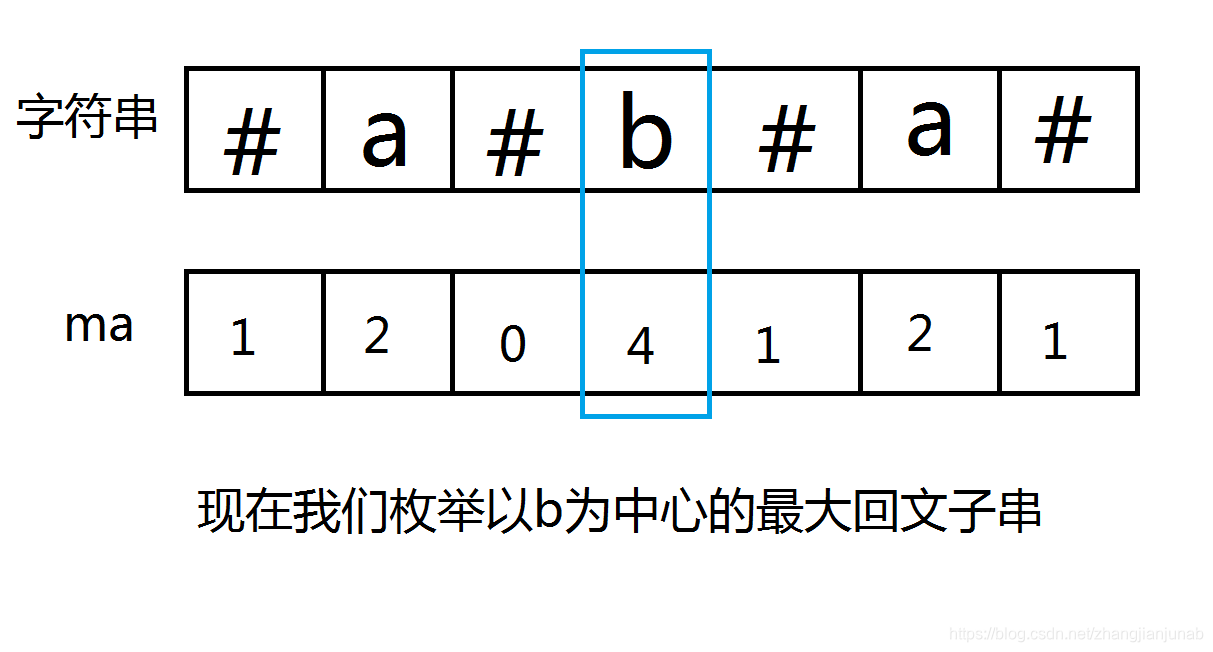
首先,我們知道,目前我們是以字母作為中心而不是'#', 那麼,在迴文子串中中心左邊的子串就呈現這種情況:#?#?#?#...#(問號是字母),而這個子串的長度是中心的ma值減1,'#'的個數是?的個數加1。
而右邊也是#?#?#?#...#(問號是字元),長度也一樣,'#'與?的個數也一樣,那麼把右邊的字母與左邊的'#'號調轉一下,我們會發現右邊的子串全是'#',而左邊只剩下一個'#'號。
那麼,根據ma陣列的定義,以字母為中心的迴文子串的長度為ma值減1。
那以'#'為中心的呢?
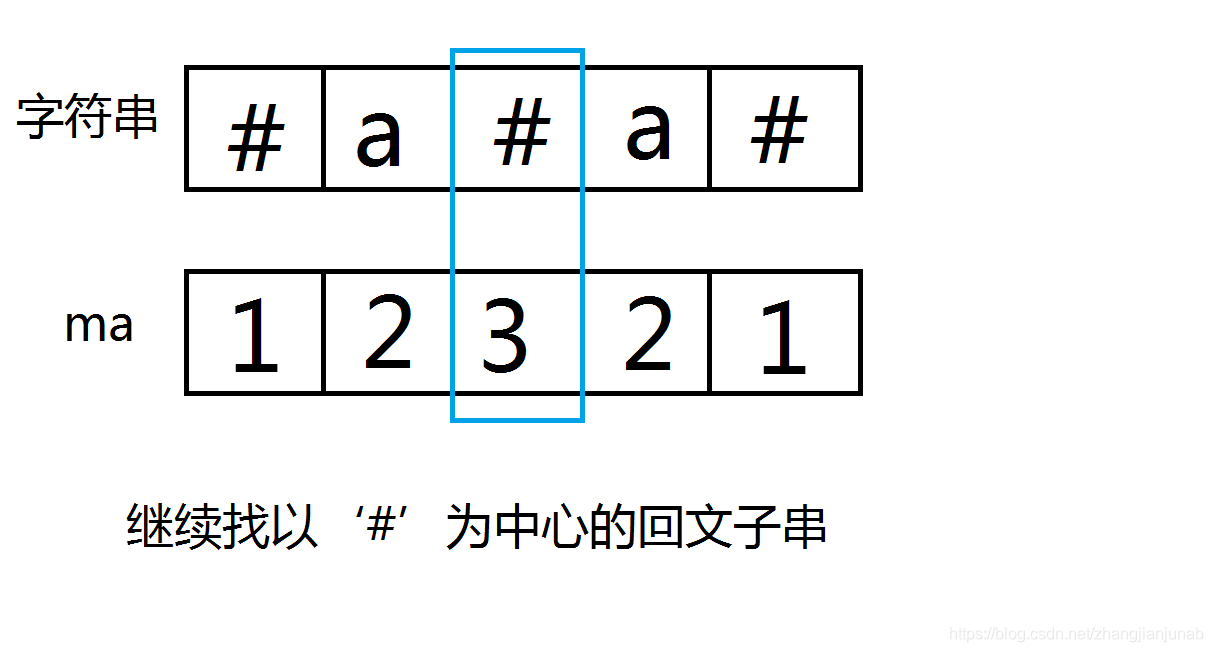
貌似也是ma值減1喲。
繼續,如果以#為中心,那麼迴文子串中心的左邊與右邊的子串也都是#?#?#?,長度為ma值減1,同時#的個數與?的個數相同,把左邊的'#'與右邊的'#'交換,那麼左邊全都是?,而中心是個'#'號,所以也是ma值減1。
處理ma陣列
沒錯,這也是最重要的!
學過EXKMP的話,這個應該是可以自己手推的。
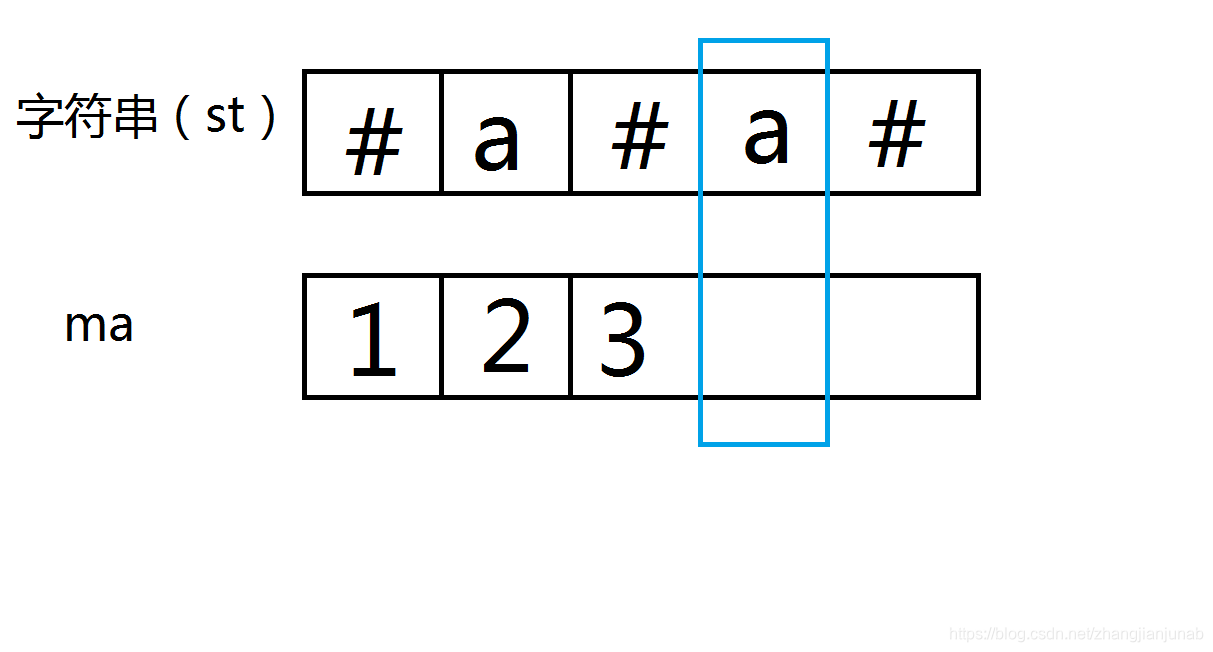
現在處理以a為中心的迴文子串,難道還要從1開始?
細心的同學發現了,由於第三個位置('#')的ma值為3,我們可以發現,\(st_{2}=st_{4},st_{1}=st_{5}\),我們可以大膽的猜想一下我們可以將\(ma_{2}\)作為一個參考,\(ma_{2}\)值為2,仔細一看,\(ma_{4}\)的值至少為2!
繼續參考EXKMP。
我們得到一下步驟:
- 統計目前回文子串能到的最遠位置(p)與是哪個中心(b)。
- 設\(L=ma_{b-(i-b)}\)
- 當\(i+L-1<p\)時,ma的值直接等於L
- 當\(i+L-1≥p\)時,ma值為\(p-i+1\),然後開始直接暴力匹配,更新b與p。
其實在\(i+L-1>p 並且 i≤p\)時,ma值其實直接等於\(p-i+1\)就可以了,不需要暴力匹配,跟EXKMP差不多。
至於更改了b與p為什麼答案還一樣,我就不一一贅述了,都跟EXKMP差不多。
現在都還不懂的話,看程式碼自行理解吧
#include<cstdio>
#include<cstring>
#define N 23000000
using namespace std;
char st[N],sst[11000000];
int ma[N],n,ans;//定義
inline int mymax(int x,int y){return x>y?x:y;}
void Man()
{
int b=0,p=0;
for(int i=1;i<=n;i++)
{
int L=ma[b-(i-b)];
if(i+L-1<p)ma[i]=L;//情況1
else
{
int pp=p-i+1<1?1:p-i+1;//至少為1
while(i-pp>=1 && i+pp<=n && st[i-pp]==st[i+pp])pp++;//(i-pp+1)-1>=1,i+pp-1+1<=n
ma[i]=pp;b=i;p=ma[b]+b-1;ans=mymax(ans,ma[i]-1);//更新
}
}
}
int main()
{
scanf("%s",sst+1);n=strlen(sst+1);
for(int i=1;i<=n;i++)st[i*2]=sst[i];
st[n*2+1]='#';for(int i=1;i<=n;i++)st[i*2-1]='#';//填'#'號
n=n*2+1;Man();//匹配
printf("%d\n",ans);
return 0;
}推介
其實Manacher在學完EXKMP後,在學一點Manacher的概念,就可以手推了,畢竟我也是在歷史課上手推的。(應該也歸功於以前學過一次)。
總之也挺好理解的,就不一一贅述了。
簡單的練習
基本上都是自己會做的。。。
Manacher一大部分的統計題都是\(O(n)\)可以統計,一般到了\(O(n^{2})\),就不大正常了,簡單的例題都是\(O(n)\)可以統計的。
在Manacher匹配中,統計每個位置為開頭或結尾的迴文子串最長是多少。
然後在後面在更新全域性:\(ll_{i}=mymax(ll_{i},ll_{i-2}-2)\)(跳過'#'),\(rr_{i}=mymax(rr_{i},rr_{i+2}-2)\)(跳過'#')。
#include<cstdio>
#include<cstring>
#include<cstdlib>
#define N 210000
using namespace std;
char st[N],stt[N];
int ma[N],f[N],n,ll[N]/*為開頭*/,rr[N]/*為結尾*/,ans;
inline int mymax(int x,int y){return x>y?x:y;}
void Man()
{
int b=0,p=0;
for(int i=1;i<=n;i++)
{
int L=ma[b-(i-b)];
if(i+L-1<p)ma[i]=L;
else
{
int pp=p-i+1<1?1:p-i+1;
while(i-pp>=1 && i+pp<=n && st[i-pp]==st[i+pp])pp++;
ma[i]=pp;b=i;p=ma[b]+b-1;
}
ll[i-ma[i]+2]=ma[i]-1;
!rr[i+ma[i]-2]?rr[i+ma[i]-2]=ma[i]-1:0;//用貪心來省時間
}
}
int main()
{
scanf("%s",stt+1);n=strlen(stt+1);
st[n*2+1]='#';for(int i=1;i<=n;i++)st[i*2]=stt[i],st[i*2-1]='#';
n=n*2+1;Man();
for(int i=2;i<n;i+=2)ll[i]=mymax(ll[i],ll[i-2]-2);
for(int i=n-1;i>=2;i-=2)rr[i]=mymax(rr[i],rr[i+2]-2);//後面遞推更新
for(int i=4;i<=n;i+=2)
{
if(rr[i-2] && ll[i])ans=mymax(ans,rr[i-2]+ll[i]);//統計答案
}
printf("%d\n",ans);//輸出
return 0;
}用類似差分統計,然後用快速冪加速一下。
#include<cstdio>
#include<cstring>
#define N 1100000
#define mod 19930726
using namespace std;
typedef long long ll;
char st[N];
int ma[N],n;
ll sum[N],ans,f[N],k;
void Man()
{
f[1]=n;
int b=0,p=0;
for(int i=1;i<=n;i++)
{
int L=ma[b-(i-b)];
if(i+L-1<p)ma[i]=L;
else
{
int pp=p-i+1<1?1:p-i+1;
while(i-pp>=1 && i+pp<=n && st[i-pp]==st[i+pp])pp++;
ma[i]=pp;b=i;p=ma[b]+b-1;
}
f[ma[i]*2+1]--;
}
}
ll kpow(ll x,ll p)//快速冪
{
ll qwq=1;
while(p)
{
if(p%2==1)qwq*=x,qwq%=mod;
x*=x;p>>=1;x%=mod;
}
return qwq;
}
int main()
{
scanf("%d%lld",&n,&k);
scanf("%s",st+1);
Man();
for(int i=1;i<=n;i+=2)f[i]+=f[i-2];//差分的字首和。
ans=1;
for(int i=n;i>=1;i--)
{
if((i&1)==0)continue;//不是'#'
sum[i]=f[i]+sum[i+2];
if(sum[i]>=k)//達到限制
{
ans*=kpow(i,k-sum[i+2]);ans%=mod;
break;//退出
}
if(i==1)//沒有
{
printf("-1\n");
return 0;
}
ans*=kpow(i,f[i]);ans%=mod;
}
printf("%lld\n",ans);//輸出
return 0;
}同樣記錄是否是開頭或結尾,然後用乘法統計,一個數字乘以一個字首和而已。
當然還是用了差分。。。
就不多講了,luogu有題解
//用了與第一題不同的統計方法
#include<cstdio>
#include<cstring>
#define N 4100
using namespace std;
char st[N],stt[N];
int ma[N],n,ll[N],rr[N];
long long ans;
void Man()
{
int b=0,p=0;
for(int i=1;i<=n;i++)
{
int L=ma[b-(i-b)];
if(i+L-1<p)ma[i]=L;
else
{
int pp=p-i+1<1?1:p-i+1;
while(i-pp>=1 && i+pp<=n && st[i-pp]==st[i+pp])pp++;
ma[i]=pp;b=i;p=b+ma[b]-1;
}
ll[i-ma[i]+1]++;ll[i]--;rr[i+ma[i]-1]++;rr[i]--;//差分
}
}
int main()
{
scanf("%s",stt+1);n=strlen(stt+1);
st[1]='#';for(int i=1;i<=n;i++)st[i*2+1]='#',st[i*2]=stt[i];
n=n*2+1;Man();//匹配
for(int i=1;i<=n;i++)ll[i]+=ll[i-1];
for(int i=n;i>=1;i--)rr[i]+=rr[i+1];//先處理每個數的和
for(int i=3;i<=n;i+=2)rr[i]+=rr[i-2];//再處理一個的字首和
for(int i=1;i<=n;i+=2)ans+=ll[i]*rr[i];//統計
printf("%lld\n",ans);
return 0;
}這裡稍微有些不同,我們不是找兩邊相等的迴文子串,而是找兩邊相反的迴文子串,如:1100。
而且必須是以'#'為中心,首先,按題意理解,迴文子串必須是偶數長度的,其二,由於換了迴文子串的定義,所以在Manacher的匹配中,以一個數字為中心也會出錯,這個很容易想為什麼,所以Manacher只找以'#'為中心的情況就是了。
#include<cstdio>
#include<cstring>
#define N 1100000
using namespace std;
char st[N],stt[N];
int ma[N],n;
long long ans;
void Man()
{
int b=0,p=0;
for(int i=1;i<=n;i+=2/*只找'#'號*/)
{
int L=ma[b-(i-b)];
if(i+L-1<p)ma[i]=L;
else
{
int pp=p-i+1<1?1:p-i+1;
while(i-pp>=1 && i+pp<=n && (st[i-pp]=='#'?1:st[i-pp]==(st[i+pp]^1)/*不同的計算方法*/))pp++;
ma[i]=pp;b=i;p=ma[b]+b-1;
}
ans+=(ma[i]-1)/2;//統計
}
}
int main()
{
scanf("%d",&n);
scanf("%s",stt+1);
st[1]='#';for(int i=1;i<=n;i++)st[i*2+1]='#',st[i*2]=stt[i];
n=n*2+1;
Man();
printf("%lld\n",ans);
return 0;
}用一個數組記錄以這個位置為開頭的最長不下降子序列的長度。
然後匹配的時候統計答案。
#include<cstdio>
#include<cstring>
#define N 210000
using namespace std;
int n,st[N],ma[N],f[N],ans;
inline int mymin(int x,int y){return x<y?x:y;}//最小值
inline int mymax(int x,int y){return x>y?x:y;}//最大值
void Man()
{
int b=0,p=0;
for(int i=1;i<=n;i++)
{
int L=ma[b-(i-b)];
if(i+L-1<p)ma[i]=L;
else
{
int pp=p-i+1<1?1:p-i+1;
while(i-pp>=1 && i+pp<=n && st[i-pp]==st[i+pp])pp++;
ma[i]=pp;b=i;p=ma[b]+b-1;
}
ans=mymax(mymin(ma[i]-1,f[i]-1),ans);//統計
}
}
int main()
{
int T;scanf("%d",&T);
while(T--)
{
ans=0;
scanf("%d",&n);
st[1]=-1;
for(int i=1;i<=n;i++)
{
scanf("%d",&st[i*2]);
st[i*2+1]=-1;
}
n=n*2+1;
//輸入
f[1]=1;
int mind=251,minid=0;
for(int i=2;i<=n;i+=2)
{
if(mind<=st[i])mind=st[i],f[i]=i-minid+2;//包括一個-1
else mind=st[i],minid=i,f[i]=2;
f[i+1]=f[i]+1;//方便後面記錄答案
}//處理最長不下降子序列
Man();
printf("%d\n",ans);
}
return 0;
}恐怖的練習
聽說是Hash+Manacher判重,不過不想做了QAQ。
這個就真的不會了QAQ,好像是Manacher+樸素統計+優化。
小結
Manacher真的是一個不錯的演算法QMQ
