• 題目
• 題目分析
• 推的過程
• 需要避免的坑
• 整體程式碼
• USACO的題解

題目

題目描述

輸入描述

Line 1: N, the number of beads
Line 2: a string of N characters, each of which is r, b, or w

輸出描述

A single line containing the maximum of number of beads that can be collected from the supplied necklace.

樣例輸入

29
wwwbbrwrbrbrrbrbrwrwwrbwrwrrb

樣例輸出

11

題目分析

考慮到迴圈的情況，簡單起見，直接把這個輸入的字串變成三個串黏在一起。考慮的串的範圍是s[n]~s[2*n-1]
實際上就是求出每個點如是切下去，往左和往右各能延伸多少，取一個最大值。本題資料不是特別大，可能暴力並非不可能，我沒有嘗試。我的想法是一個個推出來。以ans[0][i]表示在第i的節點左邊切下去，那麼左邊切口最長能延展多少；以ans[1][i]表示在第i的節點右邊切下去，那麼右邊切口最長能延展多少。

推的過程

此處以ans[0][i]為例講解。
首先第一個點ans[0][n]的求解:
先把s[n]左邊所有的通用顏色w讀掉並且記錄數字，接著記錄第一個出現的顏色字元到dif裡面，接著繼續往左掃，遇到w時長度顯然是變長的（變色），遇到和dif內顏色相同的也顯然變長，當遇到不一樣的顏色時就中止，此時的最長長度就是ans[0][n]
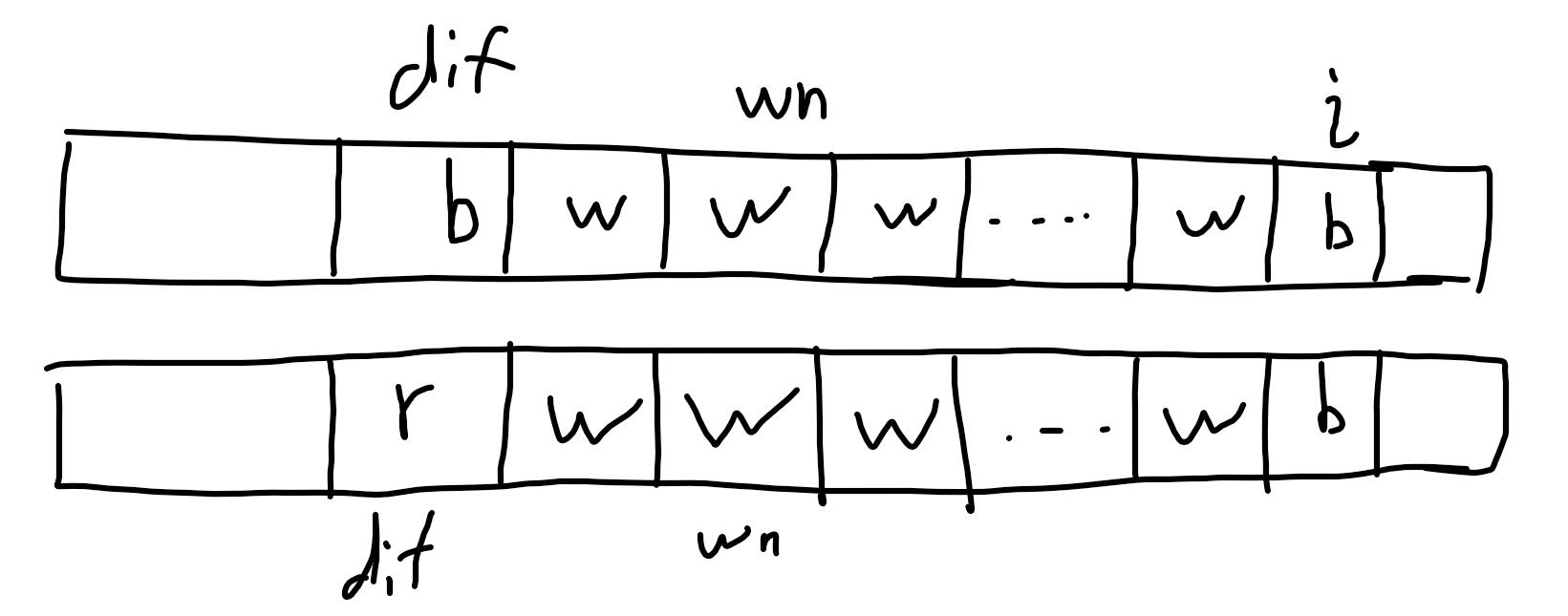
接著往右邊推了。請看我的靈魂作圖

從左往右推的過程中，需要記錄出現的最後一個非w字母是哪個字母，記在dif裡面，wn記錄連續出現了多少個w
當推到第i個位置的時候
如果i是w的話，那麼直接s[i]=s[i-1]+1（因為可以變色黏上），之後wn++
如果i不是w且和dif相同的話，那麼顯然仍然是s[i]=s[i-1]+1 （中間的w變色成和他們一樣）
如果i不是w且和dif不同的話，那s[i]=wn+1 （一串w變色成和i一樣）
注意，在第二和第三種情況下，需要將wn置零並且更新dif是哪個顏色

需要避免的坑

注意，若是隻有通用顏色w和其中某一種顏色比如說r的話，就會變成這樣
wwbbbb
那麼在最左邊切開的話，往左往右最長都能延展6個長度，那麼加起來的和就是12了，都超過串的總長了
另一種情況例如
wwbbrr，那麼從bb rr這裡切開的話，bb往左結合兩個w長度變為4，rr往右結合兩個w長度變為4，因此長度是8，也超過總長了。
這兩種情況的最優解顯然都是所有珠子都可以取到，因此若出現最大可能超過數量n的情況，答案就是n沒錯了

整體程式碼

/*
ID: penguin14
PROG: beads
LANG: C++
*/
#include<iostream>
#include <fstream>
#include<algorithm>
#include<cstring>
#include<string>
using namespace std;
string s;
int ans[2][355*3];
int main() {
    ofstream fout("beads.out");
    ifstream fin("beads.in");
    int n, r, b, i;
    int cnt;
    int wn,maxx;
    char dif;
    bool flag;
    while (fin >> n) {
        flag = true;
        fin >> s;
        s = s + s + s;
        ans[0][n] = 1;
        i = n - 1;
        while (s[i] == 'w') {
            ans[0][n]++;
            i--;
        }
        dif = s[i];
        if (i != n - 1)
            s[n-1] = dif;
        for (i--;i>=0; --i) {
            if (s[i] == dif || s[i] == 'w') {
                ans[0][n]++;
            }
            else {
                break;
            }
        }

        ans[1][2*n-1] = 1;
        i = 2*n-1;
        while (s[i] == 'w') {
            ans[1][2*n-1]++;
            i++;
        }
        dif = s[i];
        if(i!=2*n-1)
            s[2*n-1]=dif;
        for(i++;i<3*n;++i){
            if(s[i]==dif||s[i]=='w'){
                ans[1][2*n-1]++;
            }
            else{
                break;
            }
        }

        wn = 0;
        dif = s[n-1];
        for(int i=n+1;i<2*n;++i){
            if(s[i-1]=='w'){
                wn++;
                ans[0][i]=ans[0][i-1]+1;
            }else{
                if(s[i-1]==dif){
                    ans[0][i]=ans[0][i-1]+1;
                }
                else{
                    ans[0][i]=wn+1;
                }
                wn=0;
                dif=s[i-1];
            }
        }

        wn=0;
        dif = s[2*n-1];
        for(int i=2*n-2;i>=n;--i){
            if(s[i]=='w'){
                wn++;
                ans[1][i]=ans[1][i+1]+1;
            }else{
                if(s[i]==dif){
                    ans[1][i]=ans[1][i+1]+1;
                }
                else{
                    ans[1][i]=wn+1;
                }
                wn=0;
                dif=s[i];
            }
        }

        maxx=ans[0][n]+ans[1][n];
        for(int a=n+1;a<2*n;a++){
            maxx=max(maxx,ans[0][a]+ans[1][a]);
            if(maxx>=n){
                fout<<n<<endl;
                flag = false;
                break;
            }
        }
        if(flag)
            fout<<maxx<<endl;
    }
    return 0;
}

USACO的題解

USACO指出我這個實際上是dp的做法
另外，最簡單的版本，暴力是可行的