差分法是我們所用的一個強力的武器！

有這把武器你就可以統治世界。。。

一個大佬曾經講過，一但碰到區間修改的題，就要優先考慮差分。

目錄

1. 普通差分法
2. 差分套差分（二階差分）
3. 高階差分
4. 樹上差分（點的意義與邊的意義）
5. 例題

普通差分法

我們有時做題，會發現這麼一種題。

給你長度為n的序列，m次操作，有兩種：1. 讓[l,r]區間加上k。2. 查詢一個點的值。

典型的區間修改，單點查詢。
單點查詢簡單。
但是區間修改怎麼做？
暴力卡常。。。
線段樹。。。
比較正經的做法是差分，差分是什麼？

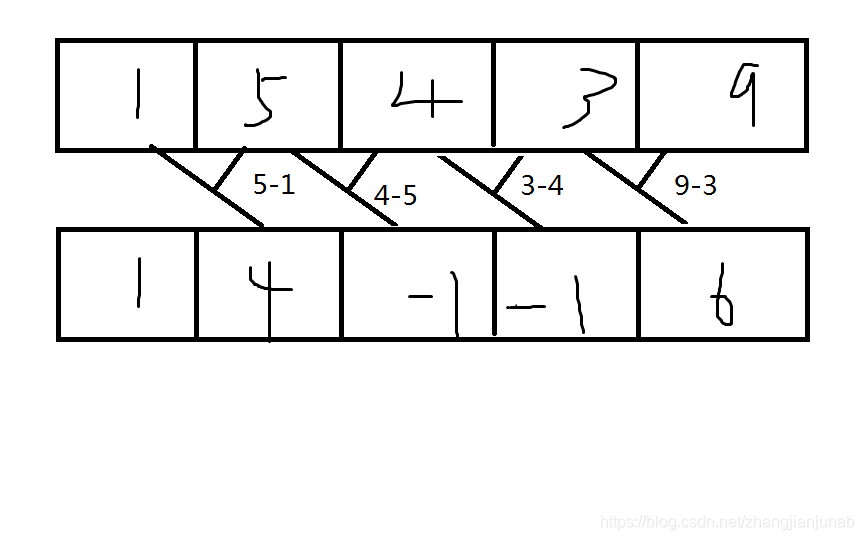
對於一個序列a，定義另一個序列b， $b$

[ i ] = a [ i ] − a [ i − 1 ] b[i]=a[i]-a[i-1] ，則叫b陣列為a陣列的差分陣列，這樣有什麼優勢呢？

首先，如果要求a[i]，我們會發現就是 $b[$

i ] + a [ i − 1 ] b[i]+a[i-1] ，不斷拆開， $a[i]=b[i]+b[i-1]+b[i-2]+b[i-3]+....+b[1]$，是不是很棒棒，就是字首和！

但是單點查詢O(n)呀

先講這樣怎麼修改，假設是 $[l,r]$區間加上k，那麼我們就讓 $b[l]$加上 $k$，讓 $b[r+1]$減去 $k$就行了。這樣，在 $[l,r]$區間內，每個數都會加上 $b[l]$多出的 $k$，但是在 $r$之後，我們也會因為 $b[r+1]$減去了 $k$從而和 $b[l]$的 $k$抵消。

這樣，區間修改就完成了！

但是單點查詢又複雜了，它可以表達成字首和，字首和…樹狀陣列維護就可以了！
是不是很不錯！

這裡給大家一點擴充套件！

至於樹狀陣列區間查詢，區間修改，我粘上一個大佬的話，我認為很不錯！

---

我們還是需要引入delta陣列，這裡的delta[i]表示區間a[i…j]都需要加上的值的和。那麼當我們需要將區間[l,r]上的每個數都加上x時，我們還是可以直接在樹狀陣列上將delta[l]加上x，delta[r+1]減去x。

那麼問題來了，如何查詢區間[l,r]的和？

我們設a[1…i]的和為sum[i]，根據delta陣列的定義，則：

$sum[i]=\sum_{j=1}^ia[j]+\sum_{j=1}^idelta[j]*(i-j+1)$
$sum[i]=\sum_{j=1}^ia[j]+(i+1)*\sum_{j=1}^idelta[j]-\sum_{j=1}^idelta[j]*j$

這樣我們就不難看sum[i]是由哪三個部分組成的了。我們需要用一個asum陣列維護a陣列的字首和，delta1與delta2兩個樹狀陣列，delta1維護delta陣列的和，delta2維護delta[i]*i的和，程式碼如下：

void add(int *arr int pos,int x){
    while(pos<=n) arr[pos]+=x,pos+=lowbit(pos);
}
void modify(int l,int r,int x){
    add(d1,l,x),add(d1,r+1,-x),add(d2,l,x*l),add(d2,r+1,-x*(r+1));
}
int getsum(int *arr,int pos){
    int sum=0;
    while(pos) sum+=arr[pos],pos-=lowbit(pos);
    return sum;
}
int query(int l,int r){
    return asum[r]+r*getsum(d1,r)-getsum(d2,r)-(asum[l-1]+l*getsum(d1,l-1)-getsum(d2,l-1));
}

摘自

---

咳咳，迴歸正題，總結一下
普通差分就是這個數減去前一個數所得到的一個數組，他不是個演算法，只是種技巧，比如在樹狀陣列中的妙用，讓樹狀陣列具有區間查詢，單點修改的功能。

差分套差分（二階差分）

沒錯你沒有聽錯，差分都可以套了！

好像又叫二階差分。

怎麼套？將差分陣列再差分一遍，求到了差分套差分的陣列，定位c陣列。

那麼，推一推，發現 $a[i]=c[i]*1+c[i-1]*2+...+c[1]*(i-1)$

嗯，這個有什麼用呢？

如果有一個毒瘤出題人，出了一道題（就是我被坑了，就寫出來了）：

給你一個長度為n的序列a，有m次操作，每次操作讓區間[l,r]分別加上t,t*2,t*3,...,t*(r-l+1)
最後輸出a序列的每個數的值

把1操作中加上的數差分，就為 $t,t,t,t,t,...,t$（注意：以後求高階差分的修改公式，將加上的陣列也進行差分來推是最好的！），那麼，就等於給a的差分陣列b區間加上t，那麼就將b再差分出另一個差分陣列c來更改，最後O(n)輸出一下答案就好了。

當然，相比差分，差分套差分會有更多應用，歡迎大家探究！

高階差分

這個就很毒瘤了，一般沒有人出這種題。講一下就是希望以後有什麼人出這種毒瘤題

我們通過列三階差分，設陣列為d，則有 $a[i]=1*d[i]+3*d[i-1]+6*d[i-2]+10*d[i-3]+...（猴子的腦子燒焦了...）$
我們觀察到 $3-1=2,6-3=3,10-6=4...$這不是二階等差數列嗎？

繼續觀察：

我們發現n階差分陣列單點查詢就等於n-1階差分陣列的字首和，也就是說，而我們發現從三階開始， $d[i]=c[i]+c[i-1]+c[i-2]..+c[1]$

相關推薦