二分與三分(精度型別)
二分:傳送門
三分:傳送門
(注意,是五舍六入,不是四捨五入,在2018年10月23日前是這樣的)
話說一本通上不是有講嘛,做法自己看吧。。。(但是我太弱了,精度版看不懂QWQ)。
簡單講一下二分與三分吧。
二分:必須滿足單調性:
非增或非減就叫單調性(如果就好幾個數相同,一般會用二分來找第一個數或最後一個數)。
我們用兩個數字l與r來代表搜尋範圍,而mid代表中間的位置的值,來跳來跳去,看情況來寫。
如這題
int l=1,r=n,mid,ans=0;
while(l<=r)
{
mid=(l+r)/2;
if(a[mid]<=m) 當然,還可以用二分來二分答案,比如你要用某種方法,但是缺少一種條件,你又意外發現這個條件越大或越小,會讓你方法越容易達到目標(也就是發現了二分性),就可以二分這個條件,不斷丟給這個方法,讓他執行。
如這題
//發現這道題如果二分總和,總和越大,分的段數就越少,越容易小於等於m,也就越容易達到目標,因此得出做法
#include<cstdio>
#include<cstring>
using namespace std; (我不是標題狗)
但是開頭的那道二分題,是要用精度的!!!
看別人的程式碼,也都是大把大把的double,醜陋的程式碼:
#include<cstdio>
#include<cstring>
using namespace std;
double a[210000],sum[210000],b[210000];
int n,L;
double mymin(double x,double y){return x<y?x:y;}
double mymax(double x,double y){return x>y?x:y;}
bool check(double x)//這個上網搜搜都是有的
{
double min_val=999999999.0,ans=-99999999.0;
for(int i=1;i<=n;i++)b[i]=a[i]-x,sum[i]=b[i]+sum[i-1];
for(int i=L;i<=n;i++)//用DP搜尋一段長度大於等於L的子串的最大和
{
min_val=mymin(min_val,sum[i-L]);
ans=mymax(ans,sum[i]-min_val);
}
return ans>=0.0;//猴子已經宕機。。。上網搜吧。。。
}
int main()
{
scanf("%d%d",&n,&L);
for(int i=1;i<=n;i++)scanf("%lf",&a[i]);
double l=-1e6,r=1e6,mid,ans=0.0,jie=1e-5;//猴子已宕機。。。
while(r-l>jie)
{
mid=(l+r)/2;
if(check(mid))ans=mid,l=mid;
else r=mid;
}
printf("%d\n",int(r*1000.0));
return 0;
}
還是上網弄了一個下來
這題可以用斜率優化做也可以用二分做,我用的是二分做法。
題意:給你n個牛的自身價值,讓你找出連續的且數量大於等於F的一段區間,使這段區間內的牛的平均價值最大。
思路:用二分列舉平均值ave,每個牛的價值都減去ave,看是否有連續的超過f長度的區間使得這段區間的價值大於等於0,如果能找到,那麼說明這個平均值可以達到。先每個a[i]減去ave得到b[i],用dp[i]表示以i為結尾區間連續長度大於等於f的最大連續區間和,maxx[i]表示以i為結尾的最大連續區間和,sum[i]表示1~i的價值總和那麼maxx[i]=max(maxx[i-1]+b[i],b[i]),dp[i]=maxx[i-f+1]+sum[i]-sum[i-f+1],判斷是否有一個i(i>=f)滿足dp[i]>=0.
作者:Herumw
來源:CSDN
原文:https://blog.csdn.net/kirito_acmer/article/details/48716719
版權宣告:本文為博主原創文章,轉載請附上博文連結!
如果你是神犇看懂了=_=。哥哥,我們不約
好的,如果你不是神犇,那麼請:
不過,有時,我們不一定要用double,我們乘以一個1000轉成int,然後在check再暫時轉回double
程式碼(摘自我機房大佬CLB的程式碼):
//Sorry,之前放錯程式碼了
#include<cstdio>
#include<cstring>
#define INF 2147483647
using namespace std;
int N,L,a[110000];
long long sum[110000];
inline bool check(int x)
{
for(int i=1;i<=N;i++) sum[i]=sum[i-1]+(a[i]-x);//減去平均值,看看總和是否能為非負數
long long minn=INF;
for(int i=L;i<=N;i++)
{
if(sum[i-L]<minn) minn=sum[i-L];
if(sum[i]-minn>=0) return true;//這裡是把拖後腿那一部分減掉,如果為正數,就表示此方案可行
}
return false;//此方案不行
}
int main()
{
scanf("%d%d",&N,&L);
for(int i=1;i<=N;i++) scanf("%d",&a[i]),a[i]*=1000;//最後結果要乘1000,為了方便計算(不算小數),就在開始直接乘了
int l,r,mid,ans;
l=0;r=2000000;
while(l<=r)//二分平均值
{
mid=(l+r)>>1;
if(check(mid)==true) l=mid+1,ans=mid;
else r=mid-1;
}
printf("%d\n",ans);
return 0;
}
到三分了,三分呢,主要解決單峰問題(求單峰),不過遞增或遞減也可以喲不過只是求第一個數或最後一個數!
所謂三分,肯定是把區間用兩個數(記作m1與m2,m1<=m2)分成三個部分(除了某些特殊情況:n=2…),然後將這兩個數比較,然後l跳到m1+1,r跳到m2-1,然後當l>r退出,由於這裡比二分還複雜,所以猴子還沒找到直接記錄答案的方法,只能最後比較l與r,雖然一次只縮小
但是總比某退火的玄學複雜度快吧。
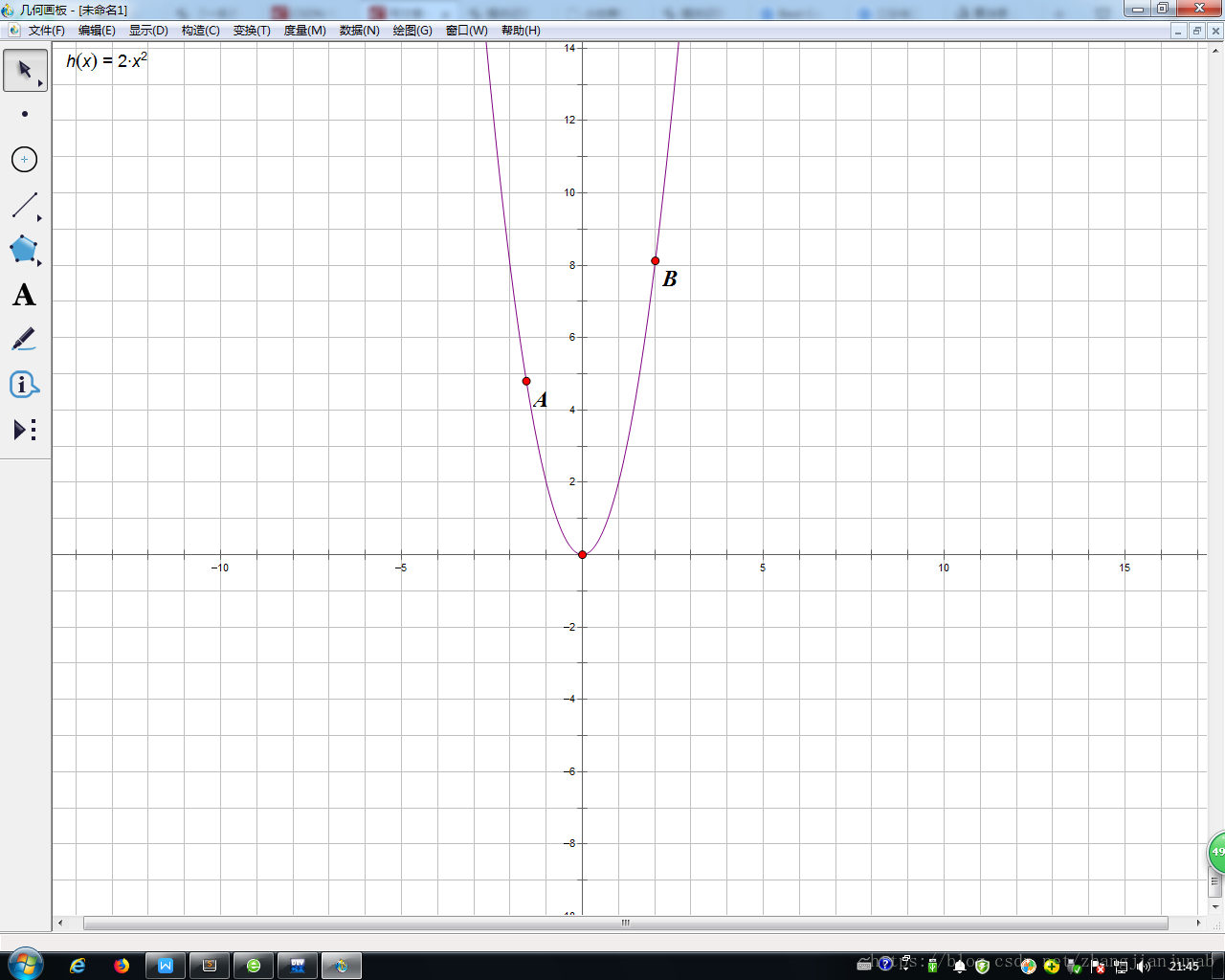
舉個栗子(二次函式:開口向上):
以x軸做三分,那麼m1(A點)的y小於m2(B點)的y,那麼我們就讓r跳到比m2小一點的地方(按題目來定),反之讓l跳到比m1大一點點的位置,來達到我們將l與r縮小的目的。
至於突然退化成一次函式的二次函式(某毒瘤出題人乾的),與二次函式的情況一樣,不過l或r有一個不變罷了。。。
偽例題:
一個序列,其中有一個數,這個數左邊的序列嚴格遞增,左邊嚴格遞減,右邊嚴格遞增。
一個整數n
n個數字
輸出這個數字:
樣例輸入:
5
1 2 3 2 1
樣例輸出:
3
int l=1,r=n,m1,m2;
while(l<=r)
{
m1=l+(r-l+1/*+1不+1都可以*/)/3/*為什麼不+1?如果l==r,m1就跳出去了,m2也是同理*/;m2=r-(r-l+1)/3;
if(a[m1]<=a[m2]/*<與<=都可以*/)r=m2-1;
else l=m1+1;//縮小範圍
}
if(a[l]<a[r])printf("%d\n",a[l]);
else printf("%d\n",a[r]);
至於如果有一段的值相等,這種情況我認為是可以的,歡迎大家再我的下方評論,畢竟三分剛學不久。。。
比如上圖。。。
然後,又到了開頭的那道三分了。。。
又是精度問題!
至於單峰性。。。
題目:給你n條開口向上的二次曲線Si(a>0),定義F(x) = max(Si(x)),求F(x)的最小值。
分析:三分。F(x)是一個單峰函式,先單調遞減後單調遞增,利用三分求最小值。
首先,證明兩個二次函式構造的F2(x)為單峰函式;
(如果不成立,則存在兩個連續的波谷,交點處一個函式遞增另一個遞減,矛盾,不會取遞減函式)
然後,用數學歸納法證明,Fi(x)為單峰函式,則Fi+1 = max(Fi(x),Si+1(x))也是單峰函式;
(如果存在兩個(或更多)連續的波谷,交點處一個函式遞增另一個遞減,矛盾,所以只有一個波谷)
結論,綜上所述得證結論,只存在一個波谷。
作者:小白菜又菜
來源:CSDN
原文:https://blog.csdn.net/mobius_strip/article/details/45618095
版權宣告:本文為博主原創文章,轉載請附上博文連結!
看不懂自己YY吧,啊啊啊啊。
難道又要動用我們毒瘤可愛的double了?
不,我拒絕!!!
既然保留四位小數,又五舍六入,那麼乘100000啦!
#include<cstdio>
#include<cstring>
using namespace std;
typedef long long ll;
ll a[200000],b[200000],c[200000],n;
inline double mymax(double x,double y){return x>y?x:y;}
inline double cai(ll x)//從所有函式中選最大值
{
double xx=x/100000.0;//變回double
double mmax=-999999999;
for(ll i=1;i<=n;i++)mmax=mymax(mmax,(a[i]*1.0)*xx*xx+(b[i]*1.0)*xx+(c[i]*1.0));
return mmax;
}
int main()
{
ll T;scanf("%lld",&T);
while(T--)
{
scanf("%lld",&n);
for(int i=1;i<=n;i++)scanf("%lld%lld%lld",&a[i],&b[i],&c[i]);
ll l=0,r=1e8/*1*10的8
次方*/,m1,m2,ans;//三分日常操作
while(l<=r)
{
m1=l+(r-l+1)/3;m2=r-(r-l+1)/3;
if(cai(m1)<=cai(m2))r=m2-1;
else l=m1+1;
}
if(cai(l)<cai(r))printf("%.4lf\n",cai(l));
else printf("%.4lf\n",cai(r));//統計答案
}
return 0;
}
。。。
作者可能學了個假的三分。。。
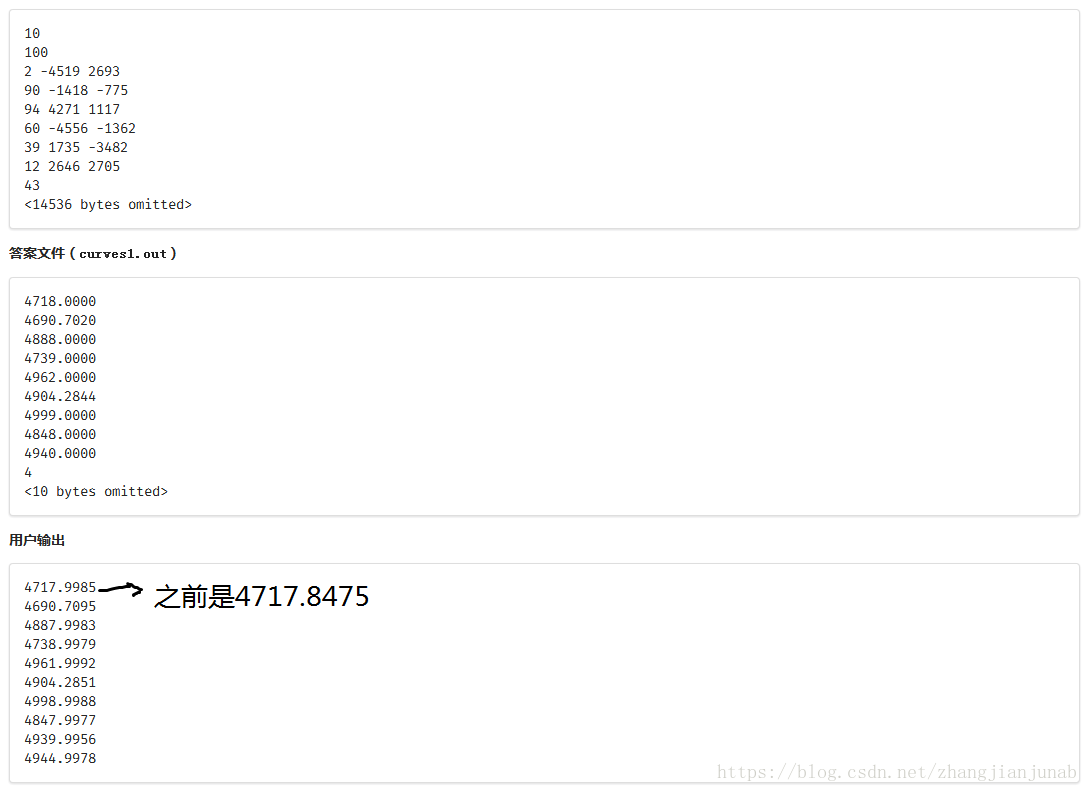
不過,如果乘以一百萬(多乘了個10)。。。
猴子(作者)想了一個壞想法,於是我用了高精度1e10與1e11,終於,在1e11時卡精度AC了!
AC程式碼:
//猴子將double*1e8將他轉為long long
#include<cstdio>
#include<cstring>
using namespace std;
typedef long long ll;
ll a[200000],b[200000],c[200000],n;
inline double mymax(double x,double y){return x>y?x:y;}
inline double cai(ll x)//轉回long long;
{
double xx=x/100000000.0;
double mmax=-999999999;
for(ll i=1;i<=n;i++)mmax=mymax(mmax,(a[i]*1.0)*xx*xx+(b[i]*1.0)*xx+(c[i]*1.0));
return mmax;
}
int main()
{
ll T;scanf("%lld",&T);
while(T--)
{
scanf("%lld",&n);
for(int i=1;i<=n;i++)scanf("%lld%lld%lld",&a[i],&b[i],&c[i]);
ll l=0,r=1e11,m1,m2,ans;
while(l<=r)
{
m1=l+(r-l+1)/3;m2=r-(r-l+1)/3;
if(cai(m1)<cai(m2))r=m2-1;
else l=m1+1;//三分
}
if(cai(l)<cai(r))printf("%.4lf\n",cai(l));
else printf("%.4lf\n",cai(r));
}
return 0;
}
所以,帶精度的二分與三分是可以轉成long long來做的,不過如果有實數乘法要在check裡再轉會double就行了,不過三分可能要多乘一點。
終於寫完了。
每日笑話:
追到我的女神 我用了三個辦法 辦法一 堅持 辦法二 不要臉 辦法三 堅持不要臉 她帶我回家 她爸爸很無禮地跟我說 我養了我女兒二十年 我憑什麼把她嫁給你 我回答 你養她二十年 我要養她四十年 還要照顧你三十年 你憑什麼不把她嫁給我
--------來源
--------來源
感謝大家觀看。
就怪了!
難道大家沒發現三分會比二分慢嗎?
啊啊啊啊啊!
但是,我們可以將m1=(l+r)/2;m2=m1+1;
這樣子,如果比較完後,l=m2或者r=m1,正確性的話雖然m1與m2靠的很近,不過依舊可以達到單峰在l與r之間,就對了,不過是l<r不是l<=r,因為這樣分m1與m2嚴格m1<m2且m1與m2屬於[l,r],所以只能用l<r,不過這樣有個好處,就是由於l或r都是等於m1或m2的,所以不會出現r<l的情況,最後一定l==r,所以答案就是l或r,而且一次縮小的區間變大了,常數也就小了!
程式碼:
#include<cstdio>
#include<cstring>
using namespace std;
typedef long long ll;
ll a[200000],b[200000],c[200000],n;
inline double mymax(double x,double y){return x>y?x:y;}
inline double cai(ll x)
{
double xx=x/100000000.0;
double mmax=-999999999;
for(ll i=1;i<=n;i++)mmax=mymax(mmax,(a[i]*1.0)*xx*xx+(b[i]*1.0)*xx+(c[i]*1.0));
return mmax;
}
int main
相關推薦
二分與三分(精度型別)
二分:傳送門 三分:傳送門 (注意,是五舍六入,不是四捨五入,在2018年10月23日前是這樣的) 話說一本通上不是有講嘛,做法自己看吧。。。(但是我太弱了,精度版看不懂QWQ)。
簡單講一下二分與三分吧。
二分:必須滿足單調性:
非增或非減就叫單調性(如果就好幾個數相同,
二分與三分查詢模板
可參考https://wenku.baidu.com/view/3f0805820740be1e650e9a8c.html
二分查詢
a[] 是有序的 成升序或降序
int find(int a[])//假定是在0到100之間搜尋 l取最左邊 r 取最右邊
【二分與三分03】Copying Books
題目來源:
題目大意:
將n本頁數為p1,p2,……,pm(順序排列)的書分給k個抄寫員抄寫,每個抄寫員速度一樣且每個抄寫員只能抄寫編號相鄰的書,求抄寫時間最少的分組。
解題思路:
二分法與貪心。
通過二分法求出一個抄寫員最多需要抄寫的頁數,然後按照這個頁數來分組
『一本通』二分與三分
span 均值 大於等於 double its 分段 check line struct 憤怒的牛
1 #include<bits/stdc++.h>
2 using namespace std;
3 int n,m,ans,a[100005];
4
HDU 2141(二分&三分 _B題)解題報告
opened span print -c name tac str 報告 nlog 題目鏈接:http://acm.hdu.edu.cn/showproblem.php?pid=2141
-------------------------------------------
HDU的一些二分和三分的一些題目(大部分模擬)
大家如果對於二分和三分沒有把握的話可以多練練,我其他的部落格文章裡面也有關於二分和三分的一些解釋。Can you solve this equation?(HDU 2199) Strange fuction(HDU 2899) Pie(HDU 1969) To
ACM之路(1)——對二分及三分的研究
對於二分來說,個人暫且將其分為整數型和實數型。 對整數型而言,一般問題對於(low<=high)條件的判斷取等號即可,因為在while途中查詢遇到可匹配的便break,比方說二分查詢已排序的數列。但是有些問題並不是這樣的,在此分為兩類:取最大值的min,和取最
XSS的原理分析與解剖:第三章(技巧篇)**************未看*****************
第二章 != chrom 插入 是把 調用 bject innerhtml ats ??0×01 前言:
關於前兩節url:
第一章:http://www.freebuf.com/articles/web/40520.html
第二章:http://www.free
POJ3977:Subset——題解(三分+折半搜索)
枚舉 cstring 不為 tdi bsp inline poj 折半 %d http://poj.org/problem?id=3977
題目大意:有一堆數,取出一些數,記他們和的絕對值為w,取的個數為n,求在w最小的情況下,n最小,並輸出w,n。
—&m
枚舉 + 三分 (遊標)
int area 存在 lan freopen 最小 numbers esp between
The swimming area of Berhattan‘s city beach is marked out with n buoys. The buoys form a
#10013 曲線 (三分法模板題)
ase ext namespace lin str scrip sel nts otto 【題目描述】
明明做作業的時候遇到了 n 個二次函數 S?i??(x)=ax?2??+bx+c,他突發奇想設計了一個新的函數 F(x)=max{Si(x)},i=1…n。
明
GNU/Linux 正則表達式與三劍俠(grep,sed,awk)(精)
重復 深入理解 不同的 原則 寬度 搜索命令 自定義 -o 排序 相關好文章推薦:
shell命令行的解析原理(單雙無引號與字符及通配符的關系):http://www.cnblogs.com/f-ck-need-u/p/7426371.html
正則表達式裏是如何表達字符集
Python(三)語法(資料型別,變數)
資料型別
整數
Python可以處理任意大小的整數,當然包括負整數,在程式中的表示方法和數學上的寫法一模一樣,例如:1,100,-8080,0,等等。
計算機由於使用二進位制,所以,有時候用十六進位制表示整數比較方便,十六進位制用0x字首和0-9,a-f表示,例如:0xff00,0xa5
c++的基本資料型別與儲存結構(學生筆記)
資料型別: 1.基本型別:整型(int,bool,enum),浮點型(float,double),字元型(char) 2.結構型別:陣列([ ]),結構(struct)聯合(union),類(class) 3.指標型別:(*) 4.空型別:(void)
整形根據示數範圍分為:短整形(sh
GNU/Linux 正則表示式與三劍俠(grep,sed,awk)(精)
相關好文章推薦:
GNU 的正則表示式
傳聞中三劍俠的威名響徹雲霄,傳說中若沒有正則表示式的神功,三劍俠也是芸芸眾生,江湖中傳言"欲成劍俠,先練神功",不管傳說或傳聞我都信。
度度果然不是蓋的,一下就拔出了正則的歷史,不看不知道,一看就大有來頭,大約就是國外幾位猛人科學家在搞一個偉大的工程時誕
BZOJ1857 傳送帶(三分套三分(難道是傳說中的。。。九分!))
【題目描述】
在一個2維平面上有兩條傳送帶,每一條傳送帶可以看成是一條線段。兩條傳送帶分別為線段AB和線段CD。lxhgww在AB上的移動速度為P,在CD上的移動速度為Q,在平面上的移動速度R。現在lxhgww想從A點走到D點,他想知道最少需要走多長時間。
【輸入格式】
三維(多維)陣列與 指標 sizeof strlen
多維陣列可以看作是一維陣列的首元素地址所組成的陣列的首元素地址所組成的陣列~~~
而且同級別的元素在連續的記憶體空間中儲存
有點暈,來看個圖
看個程式碼
輸出了arr[0]開頭的所有元素,因為a
團隊作業5——測試與發布(Alpha版本)
發布說明 實現 http 基礎 相差 還需 導致 延遲 要求 Alpha版本測試報告
一、測試找出的bug
(1)練習模式的測試
在測試中發現的bug如下:
① 連續兩個運算數當做一個處理(如1和2連續輸入當做12處理)
② 練習模式沒有提示答案
③
集美大學網絡1413第九次作業成績(團隊五) -- 測試與發布(Alpha版本)
ima worker str ges 運行 .cn png www text NO.NE團隊的項目鏈接有效,六個核桃和六指神功團隊可以請教下他們,避免因IP地址無效或者因tomcat不打開就不能訪問的情況,畢竟助教沒辦法知道此時此刻它是開著還是關閉啊啊啊。。。
題目
團隊作
團隊作業9——測試與發布(Beta版本)
登錄 iter 學生 情況 需要 上班族 監測 方法 alt Beta版本發布說明
1.在測試過程中總共發現了多少Bug?每個類別的Bug分別為多少個?
a. 修復的bug:收藏功能添加出錯。
b. 不能重現的bug:暫未發現。
c. 這個產品就是這樣設計的,不是bug:暫