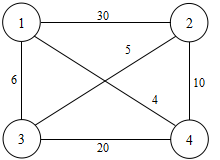
分支限界法-旅行售貨員問題
旅行售貨員問題的解空間樹是一顆排序樹。與前面關於子集樹的討論類似,實現對排列樹搜尋的優先佇列式分支限界法也可以用兩種不同的實現方式。一種是僅使用一個優先佇列來儲存活結點。優先佇列中的每個活結點都儲存從根到該活結點的相應路徑。另一種是用優先佇列來儲存活結點,並同時儲存當前已構造出的部分排列樹。在這種方式下,優先佇列中的活結點不必再儲存從根到該活結點的相應路徑,這條路徑可在必要時從儲存的部分排列樹中獲得。
輸入:城市的數目n,城市a,b,以及其之間的路程d。
輸出:最短的路程,最短的路徑方案。

在下面的討論中採用第一種方式。
在具體實現時,用鄰接矩陣表示所給的圖G。在類Traveing中用二維陣列a儲存圖G的鄰接矩陣。
template <class Type>
class Traveling
{
public:
Type BBTSP(int *v, Type **, int, Type);
private:
Type **a, //圖G的鄰接矩陣
NoEdge; //圖G的無邊標誌
int n; //圖G的頂點數
};
要找最小費用旅行售貨員迴路,選用最小堆表示活結點優先佇列。最小堆中元素的型別為MinHeapNode。該型別結點包含域x,用於記錄當前解;s表示結點在排列樹中的層次,從排列樹的根結點到該結點的路徑為x[0:s],需要進一步搜尋的頂點是x[s+1:n-1]。cc表示當前費用,lcost是子樹費用的下界,rcost是x[x:n-1]中頂點最小出邊費用和。
//佇列中元素型別 template <class Type> class MinHeapNode { template <class T> friend class Traveling; public: bool operator < (const MinHeapNode &MH) const { return lcost > MH.lcost; } private: Type rcost, //x[s:n-1]中頂點最小出邊費用和 lcost, //子樹費用的下界 cc; //當前費用 int s, //根結點到當前結點的路徑為x[0:s] *x; //需要進一步搜尋的頂點是x[s+1:n-1] };
演算法開始時建立一個最小堆,表示活結點優先佇列。堆中每個結點的lcost值是優先佇列的優先順序。接著計算出圖中每個頂點的最小費用出邊並用Minout記錄。如果所給的有向圖中某個頂點沒有出邊,則該圖不可能有迴路,演算法即告結束。如果每個頂點都有出邊,則根據計算出的Minout作演算法初始化。演算法的第一個擴充套件結點是排列樹中根結點的唯一兒子結點。在該結點處,已確定的迴路中唯一頂點為頂點1.初始時有s=0,x[0]=1,x[1:n-1]=(2,3,...,n),cc=0且 ,演算法中用bestc記錄當前最優值。
template <class Type>
Type Traveling<Type>::BBTSP(int *v, Type **G, int tn, Type tNoEdge)
{
priority_queue<MinHeapNode<Type> > pq;
MinHeapNode<Type> E, N;
Type bestc, cc, rcost, MinSum, *MinOut, b;
int i, j;
a = G;
n = tn;
NoEdge = tNoEdge;
MinSum = 0; //最小出邊費用和
MinOut = new Type[n+1]; //計算MinOut[i]=頂點i的最小出邊費用
for(i = 1; i <= n; i++)
{
MinOut[i] = NoEdge;
for(j = 1; j <= n; j++)
if(a[i][j] != NoEdge && (a[i][j] < MinOut[i] || MinOut[i] == NoEdge))
MinOut[i] = a[i][j];
if(MinOut[i] == NoEdge) //無迴路
return NoEdge;
MinSum += MinOut[i];
}
//初始化
E.s = 0;
E.cc = 0;
E.rcost = MinSum;
E.x = new int[n];
for(i = 0; i < n; i++)
E.x[i] = i+1;
bestc = NoEdge;
//搜尋排列空間樹
while(E.s < n-1) //非葉結點
{
if(E.s == n-2) //當前擴充套件結點是葉結點的父結點 再加2條邊構成迴路
{ //所構成迴路是否優於當前最優解
if(a[E.x[n-2]][E.x[n-1]] != NoEdge && a[E.x[n-1]][1] != NoEdge &&
(E.cc+a[E.x[n-2]][E.x[n-1]]+a[E.x[n-1]][1] < bestc || bestc==NoEdge))
{
//費用更小的路
bestc = E.cc + a[E.x[n-2]][E.x[n-1]] + a[E.x[n-1]][1];
E.cc = bestc;
E.lcost = bestc;
E.s++;
pq.push(E);
}
else
delete []E.x; //捨棄擴充套件結點
}
else //產生當前擴充套件結點兒子結點
{
for(i = E.s+1; i < n; i++)
if(a[E.x[E.s]][E.x[i]] != NoEdge)
{
//可行兒子結點
cc = E.cc + a[E.x[E.s]][E.x[i]]; //當前費用
rcost = E.rcost - MinOut[E.x[E.s]]; //更新最小出邊費用和
b = cc + rcost; //下界
if(b < bestc || bestc == NoEdge) //子樹可能含最優解 結點插入最小堆
{
N.s = E.s + 1;
N.cc = cc;
N.lcost = b;
N.rcost = rcost;
N.x = new int[n];
for(j = 0; j < n; j++)
N.x[j] = E.x[j];
N.x[E.s+1] = E.x[i]; //獲得新的路徑
N.x[i] = E.x[E.s+1];
pq.push(N); //加入優先佇列
}
}
delete []E.x; //完成結點擴充套件
}
if(pq.empty()) //堆已空
break;
E = pq.top(); //取下一擴充套件結點
pq.pop();
}
if(bestc == NoEdge) //無迴路
return NoEdge;
for(i = 0; i < n; i++) //將最優解複製到v[1:n]
v[i+1] = E.x[i];
while(pq.size()) //釋放最小堆中所有結點
{
E = pq.top();
pq.pop();
delete []E.x;
}
return bestc;
}演算法中while迴圈的終止條件是排列樹的葉結點成為當前擴充套件結點,當s=n-1時,已找到的迴路字首是x[0:n-1],它已包含圖G的所有n個頂點,當s=n-1時,相應的擴充套件結點表示葉結點。此時該葉結點所對應的迴路的費用等於cc和lcost的值。剩餘的活結點的lcost值不小於已找到的迴路的費用。他們都不可能導致費用更小的迴路。因此已找到的葉結點所相應的迴路是一個最小費用旅行售貨員迴路。演算法可以結束。
演算法的while迴圈體完成對排列樹內部結點的擴充套件。對於當前擴充套件結點,演算法分兩種情況處理。
當s=n-2時,當前擴充套件結點是排列樹中某個葉結點的父結點。如果該葉結點相應一條可行迴路且費用小於當前最小費用,則將該葉結點插入到優先佇列中,否則捨去該葉結點。
當s <n-2時,演算法依次產生當前擴充套件結點的所有兒子結點。當前擴充套件結點所相應的路徑是x[0:s],其可行兒子結點是從剩餘頂點x[s+1:n-1]中選取的頂點x[i],且(x[s],x[i])是有向圖G中的一條邊。對於當前擴充套件結點的每一個可行兒子結點。計算出其字首(x[0:s],x[i])的費用cc和相應的下界lcost。當lcost<bestc時,將這個可行兒子結點插入到活結點優先佇列中。
演算法結束時返回找到的最小費用,相應的最優解由陣列v給出。