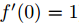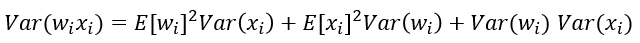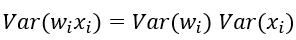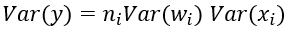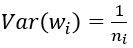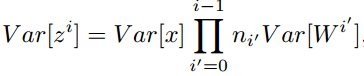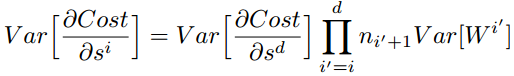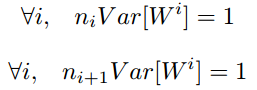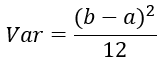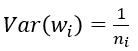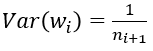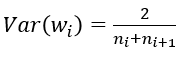Xavier初始化方法
轉載出處: https://blog.csdn.net/shuzfan/article/details/51338178
“Xavier”初始化方法是一種很有效的神經網路初始化方法,使用xavier演算法自動確定給予輸入—輸出神經元數量的初始化規模,方法來源於2010年的一篇論文《Understanding the difficulty of training deep feedforward neural networks》,可惜直到近兩年,這個方法才逐漸得到更多人的應用和認可。
為了使得網路中資訊更好的流動,每一層輸出的方差應該儘量相等。
基於這個目標,現在我們就去推導一下:每一層的權重應該滿足哪種條件。
文章先假設的是線性啟用函式,而且滿足0點處導數為1,即
現在我們先來分析一層卷積:
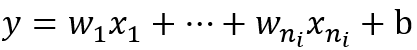
其中ni表示輸入個數。
根據概率統計知識我們有下面的方差公式:
特別的,當我們假設輸入和權重都是0均值時(目前有了BN之後,這一點也較容易滿足),上式可以簡化為:
進一步假設輸入x和權重w獨立同分布,則有:
於是,為了保證輸入與輸出方差一致,則應該有:
對於一個多層的網路,某一層的方差可以用累積的形式表達:
特別的,反向傳播計算梯度時同樣具有類似的形式:
綜上,為了保證前向傳播和反向傳播時每一層的方差一致,應滿足:
但是,實際當中輸入與輸出的個數往往不相等,於是為了均衡考量,最終我們的權重方差應滿足
———————————————————————————————————————
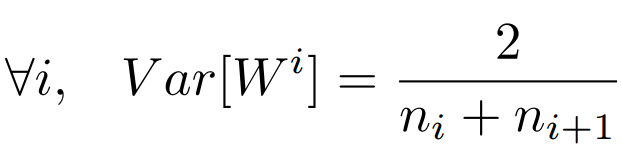
———————————————————————————————————————
學過概率統計的都知道 [a,b] 間的均勻分佈的方差為:
因此,Xavier初始化的實現就是下面的均勻分佈:
——————————————————————————————————————————
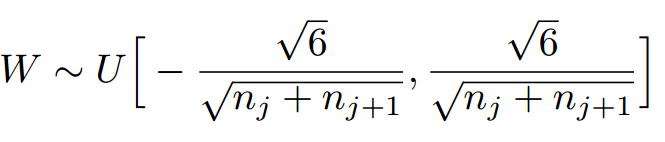
———————————————————————————————————————————
下面,我們來看一下caffe中具體是怎樣實現的,程式碼位於include/caffe/filler.hpp檔案中。
template
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
由上面可以看出,caffe的Xavier實現有三種選擇
(1) 預設情況,方差只考慮輸入個數:
(2) FillerParameter_VarianceNorm_FAN_OUT,方差只考慮輸出個數:
(3) FillerParameter_VarianceNorm_AVERAGE,方差同時考慮輸入和輸出個數:
之所以預設只考慮輸入,我個人覺得是因為前向資訊的傳播更重要一些