通常，當我提供關於GLM的課程時，我會嘗試堅持連結功能可能比分發更重要的事實。為了說明，請考慮以下資料集，並進行5次觀察

X  =  Ç（1，2，3，4，5）

Ý  =  Ç（1，2，4，2，6）

base  =  data.frame（x，y）

然後考慮幾種模型，具有各種分佈，以及一個身份連結; 在那種情況下

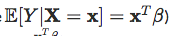
或日誌連結功能，以便：

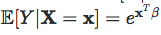
regNId  =  glm（y ~ x，family = gaussian（link = “ identity”），data = base）

regNlog  =  glm（y ~ x，family = gaussian（link = “ log”），data = base）

regPId  =  glm（y ~ x，family = poisson（link = “ identity”），data = base）

regPlog  =  glm（y ~ x，family = poisson（link = “ log”），data = base）

regGId  =  glm（y ~ x，family = Gamma（link = “ identity”），data = base）

regGlog  =  glm（y ~ x，family = Gamma（link = “ log”），data = base）

regIGId  =  glm（y ~ x，family = inverse.gaussian（link = “ identity”），data = base）

regIGlog  =  glm（y ~ x，family = inverse.gaussian（link = “ log”），data = base

人們還可以考慮一些Tweedie分佈，更為一般：

圖書館（statmod）

regTwId  =  glm（y ~ x，family = tweedie（var.power = 1.5，link.power = 1），data = base）

regTwlog  =  glm（y ~ x，family = tweedie（var.power = 1.5，link.power = 0），data = base）

考慮在第一種情況下獲得的預測，使用線性連結函式：

圖書館（RColorBrewer）

darkcols  =  brewer.pal（8，“ Dark2”）

情節（x，y，pch = 19）

abline（regNId，col = darkcols [ 1 ]）

abline（regPId，col = darkcols [ 2 ]）

abline（regGId，col = darkcols [ 3 ]）

abline（regIGId，col = darkcols [ 4 ]）

abline（regTwId，lty = 2）

預測非常接近，不是嗎？在指數預測的情況下，我們獲得：

情節（x，y，pch = 19）

û = SEQ（0.8，5.2，通過= 0.01）

行（u，predict（regNlog，newdata = data.frame（x = u），type = “ response”），col = darkcols [ 1 ]）

行（u，predict（regPlog，newdata = data.frame（x = u），type = “ response”），col = darkcols [ 2 ]）

line（u，predict（regGlog，newdata = data.frame（x = u），type = “ response”），col = darkcols [ 3 ]）

行（u，predict（regIGlog，newdata = data.frame（x = u），type = “ response”），col = darkcols [ 4 ]）

行（u，predict（regTwlog，newdata = data.frame（x = u），type = “ response”），lty = 2）

我們實際上可以看得更近。例如，線上性情況下，考慮使用Tweedie模型獲得的斜率（實際上將包括此處提到的所有引數族）。

連珠= 函式（伽馬）摘要（GLM（Ý 〜X，家族= 特威迪（var.power = 伽馬，link.power = 1），資料= 基））$ 係數 [ 2，1 ：2 ]

Vgamma  =  SEQ（- 0.5，3.5，通過= 0.05）

Vpente  =  Vectorize（pente）（Vgamma）

情節（Vgamma，Vpente [ 1，]，型別= “ L” ，LWD = 3，ylim = Ç（0.965，1.03），xlab = “ 功率”，ylab = “ 斜率”）

這裡的坡度總是非常接近一個！如果我們新增置信區間，甚至更多：

情節（Vgamma，Vpente [ 1，]）

線（Vgamma，Vpente [ 1，] + 1.96 * Vpente [ 2，]，lty = 2）

線（Vgamma，Vpente [ 1，] - 1.96 * Vpente [ 2，]，lty = 2）

啟發式地，對於Gamma迴歸或逆高斯迴歸，因為方差是預測的冪，如果預測很小（這裡在左邊），方差應該很小。因此，在圖表的左側，誤差應該很小，方差函式的功率更高。這確實是我們在這裡觀察到的。

erreur = function（gamma）predict（glm（y ~ x，family = tweedie（var.power = gamma，link.power = 1），data = base），newdata = data.frame（x = 1），type = “ 迴應“）- y [ x == 1 ]

Verreur  =  Vectorize（erreur）（Vgamma）

plot（Vgamma，Verreur，type = “ l”，lwd = 3，ylim = c（- .1，.04），xlab = “ power”，ylab = “ error”）

abline（h = 0，lty = 2）

當然，我們可以用指數模型做同樣的事情：

連珠= 函式（伽馬）摘要（GLM（Ý 〜X，家族= 特威迪（var.power = 伽馬，link.power = 0），資料= 基））$ 係數 [ 2，1 ：2 ]

Vpente  =  Vectorize（pente）（Vgamma）

plot（Vgamma，Vpente [ 1，]，type = “ l”，lwd = 3）

或者，如果我們新增置信區間，我們會得到：

plot（Vgamma，Vpente [ 1，]，ylim = c（0，.8），type = “ l”，lwd = 3，xlab = “ power”，ylab = “ slope”）

線（Vgamma，Vpente [ 1，] + 1.96 * Vpente [ 2，]，lty = 2）

線（Vgamma，Vpente [ 1，] - 1.96 * Vpente [ 2，]，lty = 2）

所以在這裡，“斜率”非常相似......如果我們看一下我們在圖的左側部分所做的錯誤，我們得到：

erreur = function（gamma）predict（glm（y ~ x，family = tweedie（var.power = gamma，link.power = 0），data = base），newdata = data.frame（x = 1），type = “ 迴應“）- y [ x == 1 ]

Verreur  =  Vectorize（erreur）（Vgamma）

plot（Vgamma，Verreur，type = “ l”，lwd = 3，ylim = c（.001，.32），xlab = “ power”，ylab = “ error”）