製造業物料清單BOM、智慧文件閱讀、科學文獻影響因子、"Celebrated Italian mathematician ZepartzatT Gozinto" 與 高津託圖
阿新 • • 發佈:2018-12-04
義大利數學家Z.高津託
義大利偉大數學家Sire Zepartzatt Gozinto的生卒年代是一個謎[1],但是他發明的 “高筋圖” 在 製造資源管理、物料清單(BOM)管理、智慧閱讀、科學文獻影響因子計算 等方面具有重要應用。
高津託圖
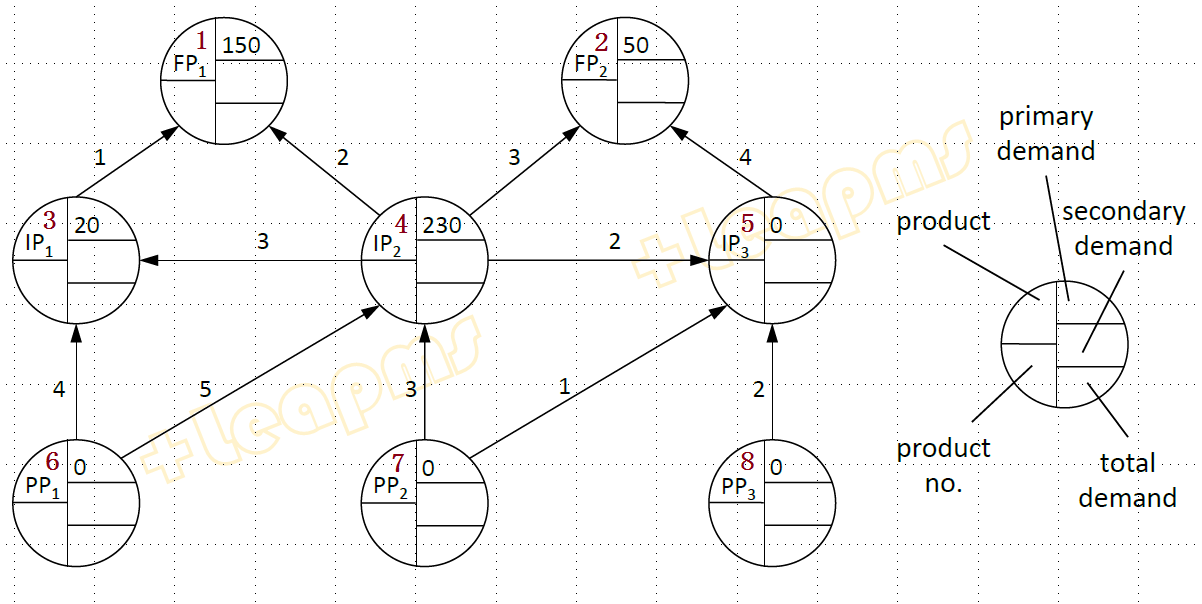
下圖是一個製造業物料需求高津託圖,節點FP1、FP2分別表示最終產品的需求量,邊上的數值表示組裝部件所需要的上游零部件的數量,物料清單(BOM)系統需要知道所有零部件的總需求。圖中:
Primary Demand(主需求) -- 市場對零部件的需求數量
Secondary Demand(次需求) -- 因產品組裝產生的對零部件的需求
Total Demand(總需求)-- 以上兩個需求之和
Product No. (產品(拓撲次序)編號)-- 根據組裝約束對零部件產品進行拓撲排序的次序數
數學模型
設圖中的零部件型別數為n,裝配關係(邊)數為m
設pd[i]為節點i的主需求(常量)
sd[i]為節點i的次需求(決策變數)
td[i]為節點i的總需求(被動變數)
pd[i]為節點i的產品拓撲次序編號(決策變數)
根據裝配邏輯,對任何邊k,如果邊k的起始節點為a[k],終止節點為b[k],權值為c[k],則:
sd[i]=sum{k=1,...,m;a[k]==i}(c[k]td[b[k]]) | i=1,...,n
td[i]=sd[i]+pd[i]|i=1,...,n把零部件從裝配上游到下游排序:
pn[b[k]] >= pn[a[k]] + 1 | k=1,...,m
pn[i]>=1|i=1,...,n
pn[i]<=n|i=1,...,n
+Leapms模型:
min sum{i=1,...,n}pn[i]
subject to
sd[i]=sum{k=1,...,m;a[k]==i}(c[k]td[b[k]]) | i=1,...,n
td[i]=sd[i]+pd[i]|i=1,...,n
pn[b[k]] >= pn[a[k]] + 1 | k=1,...,m
pn[i]>=1|i=1,...,n
pn[i]<=n|i=1,...,n
where
m,n are numbers
e,pd are sets
a[k],b[k],c[k] are numbers | k=1,...,m
sd[i],td[i] are variables of nonnegative numbers|i=1,...,n
pn[i] is a variable of nonnegative number|i=1,...,n
data_relation
m=_$(e)/3
n=_$(pd)
a[k]=e[3k-2]|k=1,...,m
b[k]=e[3k-1]|k=1,...,m
c[k]=e[3k] |k=1,...,m
data
pd={150 50 20 230 0 0 0 0}
e={
3 1 1
4 1 2
4 2 3
4 3 3
4 5 2
5 2 4
6 3 4
6 4 5
7 4 3
7 5 1
8 5 2
}求解:
+Leapms>load
Current directory is "ROOT".
.........
gozinto.leap
.........
please input the filename:gozinto
================================================================
1: min sum{i=1,...,n}pn[i]
2: subject to
3:
4: sd[i]=sum{k=1,...,m;a[k]==i}(c[k]td[b[k]]) | i=1,...,n
5: td[i]=sd[i]+pd[i]|i=1,...,n
6:
7: pn[b[k]] >= pn[a[k]] + 1 | k=1,...,m
8: pn[i]>=1|i=1,...,n
9: pn[i]<=n|i=1,...,n
10:
11: where
12: m,n are numbers
13: e,pd are sets
14: a[k],b[k],c[k] are numbers | k=1,...,m
15: sd[i],td[i] are variables of nonnegative numbers|i=1,...,n
16: pn[i] is a variable of nonnegative number|i=1,...,n
17:
18: data_relation
19: m=_$(e)/3
20: n=_$(pd)
21: a[k]=e[3k-2]|k=1,...,m
22: b[k]=e[3k-1]|k=1,...,m
23: c[k]=e[3k] |k=1,...,m
24: data
25: pd={150 50 20 230 0 0 0 0}
26: e={
27: 3 1 1
28: 4 1 2
29: 4 2 3
30: 4 3 3
31: 4 5 2
32: 5 2 4
33: 6 3 4
34: 6 4 5
35: 7 4 3
36: 7 5 1
37: 8 5 2
38: }
================================================================
>>end of the file.
Parsing model:
1D
2R
3V
4O
5C
6S
7End.
..................................
number of variables=24
number of constraints=43
..................................
+Leapms>solve
The LP is solved to optimal.
找到線性規劃最優解.非零變數值和最優目標值如下:
.........
pn1*=4
pn2*=4
pn3*=3
pn4*=2
pn5*=3
pn6*=1
pn7*=1
pn8*=1
sd3*=150
sd4*=1360
sd5*=200
sd6*=8630
sd7*=4970
sd8*=400
td1*=150
td2*=50
td3*=170
td4*=1590
td5*=200
td6*=8630
td7*=4970
td8*=400
.........
Objective*=19
.........
+Leapms>
結果
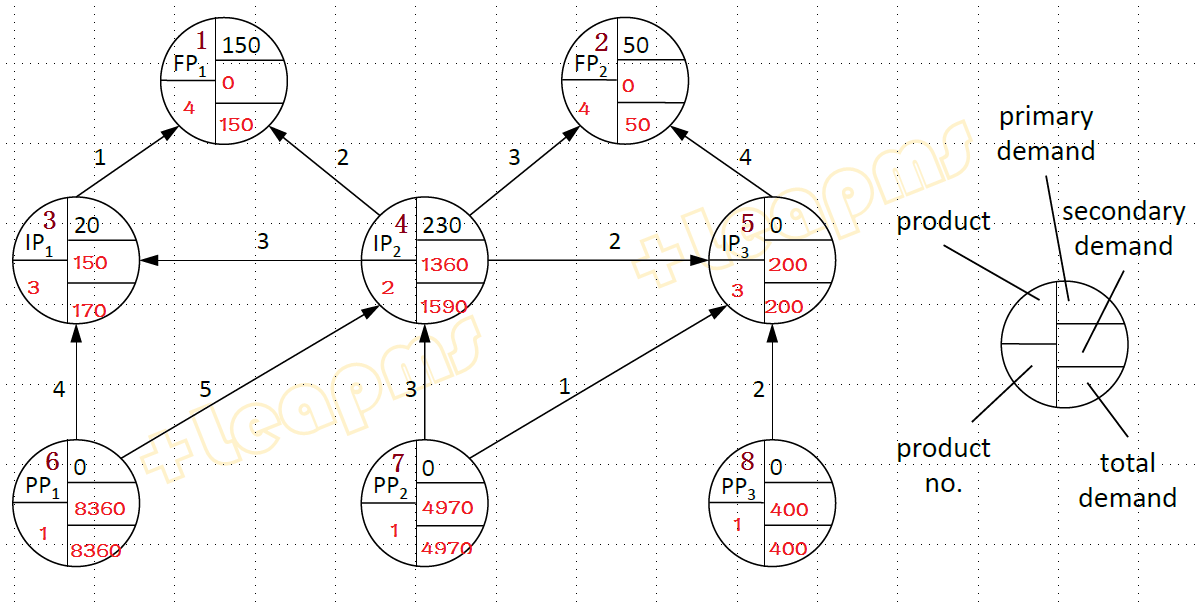
參考文獻
[1] Rousseau, R. . (1987). The gozinto theorem: using citations to determine influences on a scientific publication. Scientometrics, 11(3-4), 217-229.
