解題報告 (二) 強連通和2-sat
強連通分量題集
1)迷宮城堡
題意:給定N個點M條邊(N <= 10000, M<= 100000),問是否存在任意的點對(i, j)使得i能夠到j,並且j也能夠到i。存在輸出Yes,否則輸出No。
題解:強連通分量的定義題。對原圖求一次強連通,如果強連通分量為1,輸出Yes,否則No。
題意:給定N個點M條邊(N <= 20000, M<= 50000),問最少新增多少條邊,使得該圖的強連通分量為1。
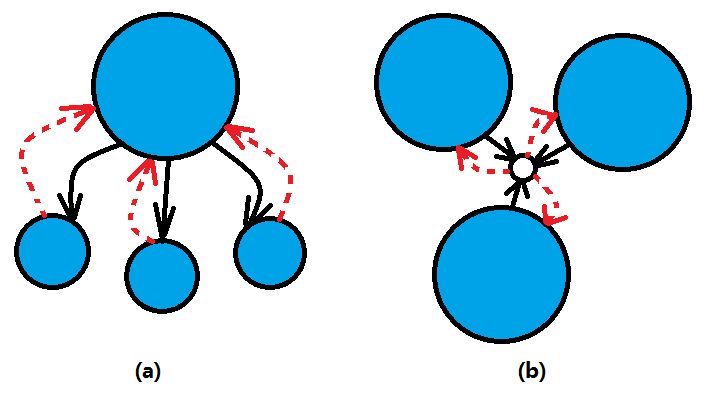
題解:對原圖求一次強連通,如果強連通分量個數已經為1,則不需要新增邊;否則,進行縮圖,縮完後的圖統計兩個量:入度為0的點的個數x,出度為0的點的個數y,需要新增的邊數為max(x, y)。如圖1所示,藍色圈中的頂點屬於同一個強連通分量,紅色虛線代表需要新增的邊。從圖中可以看出需要新增的邊只和入度為0或者出度為0的頂點有關。
圖1
題意:給定N個點M條邊(N <= 50000, M<= 100000)的有向帶權圖,如果圖中任意兩點可達,則這兩點之間的權為0。求從0號結點出發經過所有點的最小路徑和。
題解:有向圖強連通 + 最小生成樹。首先求出強連通,然後對縮點後的圖求一次最小生成樹。注意是有向圖,所以不能用Kruscal演算法,只能用Prim求最小生成樹。
5)Cactus
題意:給定N個點M條邊(N <= 20000, M<= 50000)的有向圖,如果這個圖是一個強連通圖,並且每條邊屬於一個環,則被稱為Cactus,輸出YES;否則NO。
題解:有向圖強連通 + BFS。首先求出強連通,如果連通分量個數大於1,直接輸出NO;如果強連通分量為1,並且存在重邊(如圖2中的a->b),那麼表明b經過一系列路徑到達a的邊一定屬於至少兩個環,輸出NO;。
圖2
然後列舉每條邊未被標記的邊<a=>b>,並且將它標記掉,然後從未標記掉的邊中找一條從b到a的路徑,並且將這條路徑標記掉,這一步稱為“刪圈”。直到所有的邊都被標記完畢,則這個圖為Cactus,輸出YES;如果在中途某一步找不到圈,說明有些屬於兩個圈的邊已經被刪了,則這個圖不是Cactus,輸出NO。
題意:給定N個人,M條關係(N <=1000, M<= 2000),,如果a到b有邊則表示第a個人能夠聯絡到第b個人,聯絡第i個人的花費為v[i],聯絡具有傳遞性。現在需要聯絡到所有人,求最小聯絡人數和最小花費。
題解:首先求出強連通分量,同一個連通分量中的人肯定取花費最小的那個人聯絡,這樣整個連通分量的人都能聯絡到;將原圖進行縮圖,這樣新圖變成了一個有向無環圖,那麼必然存在一些點的入度為0,只要選擇入度為0的這些點進行聯絡之後,其它人都可以通過傳遞性都聯絡到了。所以遍歷新圖找出入度為0的點累加該連通分量中的最小花費就是最後的答案了。
如圖3所示,123所在強連通分量中選擇花費最小的點以及4所在強連通分量(就是4本身)的最小化費之和就是最後的答案。
這題的詳細解釋參見文字引例:有向圖強連通例題解析
圖3
2-sat題集
1)Party
題意:有N(N <= 1000)對夫妻被邀請參加一個聚會,因為場地的問題,每對夫妻中只有1人可以列席。在2N個人中,某些人之間有著很大的矛盾(當然夫妻之間是沒有矛盾的),有矛盾的2個人是不會同時出現在聚會上的。有沒有可能會有N 個人同時列席?如果可能,輸出YES,否則NO。
首先輸入N和M(M<= 1000000);在接下來的M行中,每行會有4個數字,分別是 A1,A2, C1,C2,其中A1,A2分別表示是夫妻的編號;C1,C2 表示是妻子還是丈夫 ,0表示妻子 ,1是丈夫(夫妻編號從0到N -1 )。
題解:首先將每對夫妻看成是四個點,分別定義如下:
圖4
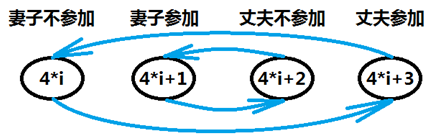
其中i的取值為[0, N),所以總的結點數為4N。我們為了方便處理,將“不參加”的結點定義為偶數編號,將“參加”的結點定義為奇數編號;並且,妻子編號模4為(0,1),丈夫編號模4為(2, 3)。每個結點可以表示成如下通項:
圖5
i代表第i對夫妻;j代表是妻子還是丈夫;k代表是否參加,這種編碼方式的好處就是可以很方便的進行索引。
然後根據題中的關係,夫妻之間只有一人可以出席,並且需要N個人同時列席。也就是說需要滿足四條關係式:
1.妻子不參加 => 丈夫必須參加;
2.妻子參加 => 丈夫必須不參加;
3.丈夫不參加 => 妻子必須參加;
4.丈夫參加 => 妻子必須不參加;
然後對於每對夫妻,建立如圖所示的四條邊:
圖6
然後再來看M個條件:A1, A2, C1,C2,其中A1,A2分別表示夫妻的編號;C1,C2 表示是妻子還是丈夫 ,0表示妻子。這裡隱含著四個結點:
Node(A1, C1, 0) 代表 第A1對夫妻中C1成員不參加;
Node(A1, C1, 1) 代表 第A1對夫妻中C1成員參加;
Node(A2, C2, 0) 代表 第A2對夫妻中C2成員不參加;
Node(A2, C2, 1) 代表 第A2對夫妻中C2成員參加;
因為(第A1對夫妻中C1成員)和(第A2對夫妻中C2成員)不能同時參加,則代表如果一個參加了,另一個必定不能參加。所以對這四個結點建立兩條邊,如下:
Node(A1, C1, 1) => Node(A2, C2, 0)
Node(A2, C2, 1) => Node(A1, C1, 0)
這樣,所有的邊建完後,總共就是4N個點,2M+4N條邊,求一次強連通,然後遍歷所有的結點,如果存在某個人“參加”和“不參加”代表的結點出現在同一個強連通分量中,說明他“參加”能夠推匯出“不參加”,“不參加”又能推匯出“參加”,與事實矛盾,則輸出NO,否則輸出YES。
2)Wedding
題意:新娘,新郎和n對夫婦,分別坐在長條桌的兩邊,其中有m對人之間存在姦情(同性和異性皆有可能)。現在有兩個限制:
1. 任意一對夫婦必須坐在長條桌的兩面;
求一種可能的方案,使得上面兩種情況都能滿足。
題解:對於第2種情況,有兩種選擇:第一種是將有姦情的人拆開坐到桌子的兩面;第二種就是將他們和新娘坐在同一面。
將每個人拆成兩個點i和i’,i代表坐左邊,i’代表坐右邊。定義每條邊a=>b的含義為如果a坐左邊,那麼b也坐左邊。那麼這樣約定以後,我們把新娘放到左邊,做法就是 0h=>0w,即新郎到新娘連一條邊,表示如果新郎坐左邊,那麼讓新娘坐左邊,讓新郎坐右邊去。對於每對姦情(a, b),建立兩條邊(a’=>b)和(b’=>a),即如果a坐右邊,那麼b必須坐左邊;如果b坐右邊,那麼a必須坐左邊。
然後求一次強連通,判斷是否存在一對夫妻在同一個強連通分量中,如果存在,則上述坐法不存在。否則採用2-sat經典演算法求一次拓撲排序即可。
題意:N個候選人進行選舉,需要滿足M個條件(N <=1000,M <= 1000000),條件型別分為四種:
1. +i +j i和j至少一人被選中;
2. -i -j i和j至少一人不被選中;
3. +i -j i被選中 或 j不被選中;
4. -i +j i不被選中 或 j被選中;
問是否存在這樣一種選舉方式,滿足所有M個條件。
題解:將每個人拆成兩個點:i表示被選中,i’表示未被選中。以上四種情況都是兩個人的選中和不選中的“或”:a or b。
a or b 等價於 (a’=>b) and (b’=>a)。每一個條件對應於兩條邊。其中a的取值為i或i’,b的取值為j或j’,代入等價式建立相應的邊即可。然後求一次強連通,如果存在i和i’在同一個強連通分量,則與條件矛盾。
題意:給定一些關係式a op b = c。其中op的取值為(AND, OR, XOR),a,b,c的取值為[0,1],其中a和b為未知數,給定未知數和關係式的個數,求是否存在這樣一種解滿足所有關係式,存在輸出YES,否則NO。
題解:三種操作符×兩種值,總共六種情況,把每個頂點X拆成兩個點x和x’,分別代表1和0,然後分情況討論:
1. a OR b = 1,這種是最經典的情況,建邊:(a’=>b)和(b’=>a),含義是如果a為0,那麼b必須為1,同樣,如果b為0,那麼a必須為1;
2. a OR b = 0,當且僅當a和b均為0時滿足,所以建邊(a=>a’)和(b=>b’),含義是無論如何a必須為0,b亦然;
3. a AND b = 1,當且僅當a和b均為1時滿足,建邊(a’=>a)和(b’=>b),含義和第2種情況正好相反;
4. a AND b = 0,建邊(a=>b’)和(b=>a’),含義和第1種情況相反;
5. a XOR b = 1,這種情況需要建四條邊,即a為0或1,b的情況;以及b為0或1時,a的情況;(a’=>b)、(b’=>a)、(a=>b’)和(b=>a’);
6. a XOR b = 0,參考第5種情況。
建完圖後求一次強連通,如果存在兩個點x和x’在同一個強連通分量中,說明無解,則輸出NO,否則YES。
題意:給定N個時間段[Si, Ti]和對應的時間間隔Di,對於每個時間段可以選擇[Si, Si+Di]或者[Ti-Di, Ti](即開始和結束)舉行一個活動。問是否存在一種方案,使得N(N <= 1000)個活動都能舉行(任意兩個活動在時間上不能有交集)。
題解:將每個時間段拆成兩個點:i表示[Si, Si+Di],i’表示[Ti-Di, Ti]。總共2000個點進行一次O(N^2)的區間兩兩判交。如果第i個時間區間和第j個時間區間有交集(邊界重合不算),則建邊(i=>j’),即第i個選的情況下,第j個不能選所以只能選j’。
然後求一次強連通,如果存在兩個點i和i’在同一個強連通分量中,則輸出NO;否則輸出YES,然後採用2-sat對收縮後的反圖求一次拓撲排序,輸出路徑。
需要注意一點,輸出的時候需要對頂點進行排序,因為題目是Special Judge,它進行資料判定可行性的時候肯定是一一對應的去判的,所以需要輸出的解也是排好序的。
6)Ikki's Story IV - Panda'sTrick
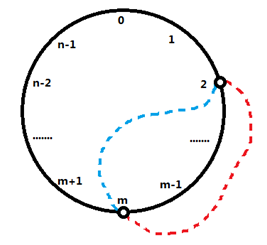
題意:一個圓上有n(n <= 1000)個結點,分別按順序編號0,1,2…n-1,從圓上任意找兩個點串起來,可以選擇從圓裡穿過(圖7中藍色虛線所示),也可以選擇從圓外穿過(圖7中紅色虛線所示),每個結點只允許連一次。給定m對連線,問是否存在這樣一種情況,所得所有連線之間互不相交。
圖7
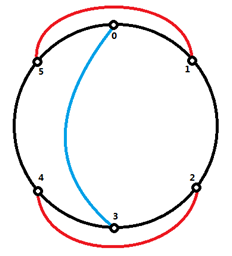
如圖8,6個結點的情況,0<->3,1<->5,2<->4 連線的情況如下。
圖8
題解:每個連線有兩種情況,所以將每個連線拆成兩個點x和x’,x代表藍色連線,x’代表紅色連線,然後就是判斷圓內直線相交了,如果兩個連線在圓內相交,那麼說明他們不能同時用藍色的連線方式,圓外亦然。所以如果兩個連線相交,那麼需要建立四條邊,即:如果我選藍,你就只能選紅,等等。
(x=>y’)、(x’=>y)、(y=>x’)、(y’=>x),有點類似 XOR 的建邊方式。
然後求一次強連通,如果存在兩個點x和x’在同一個強連通分量中,則答案為NO;否則YES。
題意:N(N <= 1024)對鑰匙(Ai, Bi),M(M <= 2048)扇門,第i扇門用(Xi, Yi)表示,代表它只能由鑰匙Xi或者鑰匙Yi開啟。
求用一種方案,從N對鑰匙中取出N個鑰匙(每對只能取一個),按順序開門開啟儘量多的門,求能夠開啟最多的門的個數。
題解:思路是這樣的:首先要開啟第i扇門必須先開啟前i-1扇門,所以可以先二分一個需要開啟的門的數量,對於第i扇門(Xi, Yi),如果Xi這個鑰匙沒有選,那麼Yi這個鑰匙必選;同樣,如果Yi這個鑰匙沒選,那麼Xi這個鑰匙必選。
每個鑰匙看成圖的一個頂點,建好圖後求強連通判可行即可。
題意:Get Luffy Out的加強版,每個鑰匙有可能出現在不同的鑰匙對中。
題解:首先還是二分答案。然後拆點,總共2N把鑰匙,拆成4N個點,分別表示這個鑰匙的取或不取。然後兩種情況建邊:
1.對於每對鑰匙(x, y),如果x取,則y不取;同理,如果y取,則x不取;
2.對於每扇門(a, b),如果a不取,則b必須取;如果b不取,則a必須取;
9)Building roads(推薦)
題意:如圖9-(1),有兩個中轉點S1和S2,以及N(N <= 500)個灰色點,現在要求把灰色點和中轉點連起來,每個灰色點要麼連S1,要麼連S2。如圖9-(2),藍色線連S1,紅色線連S2,連線的距離定義為“曼哈頓距離”,兩個灰色點之間的距離定義如下:
1.如果兩個點連線的是同一個中轉點,那麼他們的距離為各自到中轉點的距離之和,如圖9-(3)所示;
2.如果兩個點連線的不是同一個中轉點,那麼他們的距離為各自到中轉點距離之和加上兩個中轉點之間的距離,如圖9-(4)。
還有一些限制條件,給定一些灰色點必須連線到同一個中轉點,以及一些灰色點必須連線到不同的中轉點。
現在需要使得任意兩個灰色結點之間的最大距離最小,求這個最大距離。
圖9
題解:將每個灰色的點拆成兩個點x和x’,x表示連線到S1,x’表示連線到S2。總共2N個結點,將距離計算出來預處理到陣列dist[i][j],表示第i點和第j個點的距離(注意:這裡的距離不是單純的曼哈頓距離,需要算上分別連線到中轉點的距離之和)。
然後二分一個距離d,如果dist[i][j] > d,則建邊(i=>j’)和(j=>i’)。然後必須連線到同一個中轉點的點對建四條邊,必須連線到不同中轉點的點對也建四條邊。
然後強連通判可行即可。
10)Go Deeper
題意:給定這樣一個遞迴的程式,其中x[n]陣列為未知數,並且取值只有0或1;a[m]、b[m]、c[m]為給定陣列,其中0 <= a[i], b[i] < n,0 <= c[i] <= 2,並且n<=200, m<=10000。求這個程式能夠輸出的最大的dep的值。
題解:雖然是個遞迴程式,但是它沒有分叉,所以還是線性的。也就是一旦滿足dep = m或者x[a[dep]] + x[b[dep]] == c[dep],函式就返回了。所以我們要做的就是將x[i]設定為合適的值,使得它能夠滿足的條件儘量多。
首先二分dep,考慮到x[i]只有0和1兩種取值,所以可以把每個x[i]拆成兩個分別代表0和1的點,然後根據c[j] (0<=j < dep)的值(0, 1, 2)分情況建邊即可。建邊方式可以參考Katu Puzzle。
建完邊,求一次強連通分量,利用分拆的兩個點是否在同一個強連通分量中來判定二分可行性。
題意:題意圍繞“剪刀石頭布”而展開,給出Bob的N(N <=10^5)次出法(1代表石頭、2代表紙、3代表剪刀),Alice需要滿足M(M <= 10^5)個條件,條件分兩種:
1、a b 0 第a次和第b次出法必須相同;
2、a b 1 第a次和第b次出法必須不同;
如果Alice在這N次對決中,沒有一次輸才算贏,問是否存在這樣一種出法是的Alice獲勝。
題解:Alice的每次出法都有兩種選擇:要麼和Bob出的一樣,要麼贏過Bob;將這兩種出法拆成兩個點,總共2N個點,然後根據M個條件建立有向邊。
1、 第a次和第b次出法必須相同,所以列舉第a次的兩種情況和第b次的兩種情況進行兩兩組合,如果出法不同則建邊;
2、 第a次和第b次出法必須不同,所以列舉第a次的兩種情況和第b次的兩種情況進行兩兩組合,如果出法相同則建邊;
建完邊,求一次強連通判可行即可。
12)Bomb Game
題意:給定N組圓心(每組兩個),要求選擇N個圓心畫圓(其中第2K和2K+1個不能同時選擇),半徑R可以由你控制,求最大的半徑R使得所有圓不相交。
題解:首先,同一個組的圓分別記為圓i和圓i’。然後二分半徑R,然後判斷任意兩個圓是否相交,如果圓i和圓j相交,則建兩條邊(i=>j’)和(j=>i’)。
建完邊,求一次強連通判可行從而調整半徑R。
題意:給定一個N(N <= 100)個點的有向圖,求能否將圖分成兩個“完全子圖”(“完全子圖”的定義為任意兩個點都有邊)。
題解:首先將原圖的邊關係存在鄰接矩陣mat[i][j]中,mat[i][j]=1表示第i個點到第j個點有邊;然後將每個點拆成兩個點i和i’,分別表示屬於兩個子圖。然後列舉任意兩個頂點i, j,如果他們屬於屬於同一個子圖,那麼必須滿足他們所代表的的原圖中的點互相可達,如果不滿足,則建邊(i=>j’),代表i選了這個子圖,那麼j必須選另一個子圖。
建完邊求一次強連通,判可行即可。
題意:ACM集訓隊到了寒假需要回家過年,每一個隊(三人一隊)或者隊長留下或者其餘兩名隊員同時留下;每一對隊員,如果隊員A留下,則隊員B必須回家休息下,或者B留下,A回家。求是否能滿足這樣的情況。
題解:比較裸的2-sat。總共三類邊:
1、 對於每個隊伍,隊長回家,則其餘兩人必須同時留下;
2、 對於每個隊伍,隊員回家,則另一名隊員也必須回家,隊長必須留下;
3、 對於每對隊員,A留下,則B回家;B留下,則A回家;
每個隊員拆成兩個點x代表回家,x’代表留下。按照上面三種規則建邊即可。然後求一次強連通判斷可行性。
15)Map Labeler
題意:二維平面上有N個點,每個點可以生成兩個正方形,但是隻能選擇生成一個,並且該點需要位於正方形的“頂邊中點”或“底邊中點”。正方形的邊長R可以隨意控制,但是需要保證所有生成的正方形互不相交。求最大的邊長R。
題解:首先二分邊長R,然後按照規則生成所有的正方形總共2N個,第i組正方形編號分別為2i和2i+1,然後利用矩形判交把兩兩有交集的正方形建邊。
求一次強連通判可行即可,類似Bomb Game。
題意:N(N <= 8000)個黨派要各自派1名代表參加一個會議,每個黨派有兩個代表,M(M <= 100000)對代表之間不喜歡對方,所以他們不能同時出現在會議上,問一種可行方案,使得所有黨派都正好有一名代表參加會議,並且輸出字典序最小的。
題解:2-sat建邊後,從小到大列舉點選取。