損失函式

經典損失函式

分類問題和迴歸問題是監督學習的兩大種類。

1. 分類問題——將不同的樣本分到事先定義好的類別中。

• 交叉熵（cross entropy）：刻畫兩個概率分佈之間的距離，是分類問題中使用較為廣泛的一種損失函式。
  (1)Softmax迴歸，可以將神經網路的輸出轉化為一個概率分佈
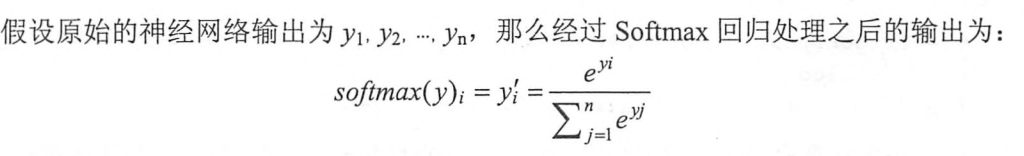  tensorflow中提供了交叉熵和Softmax兩個功能的函式tf.nn.sparse_softmax_cross_entropy_with_logits

2. 迴歸問題——對具體數值的預測，例如房價預測、銷量預測等，這些問題預測的不是一個實現定義好的分類，而是一個實數。

• 迴歸問題最常用的損失函式是均方根誤差（Mean Squared Error）
  TensorFlow中實現均方根誤差損失函式：
  

3.自定義損失函式
TensorFlow可以優化任意的自定義損失函式。

神經網路優化演算法

反向傳播演算法（backpropagation）——訓練神經網路的核心演算法，根據定義好的損失函式優化神經網路中引數的取值，從而使訓練集的損失函式達到一個較小值。
梯度下降演算法（gradient decent）——主要用於優化單個引數的取值。
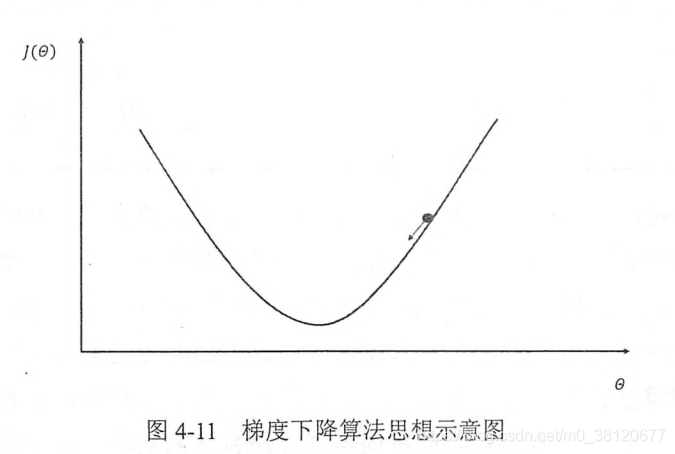梯度下降演算法並不能保證被優化的函式達到全域性最優解，如下圖所示。

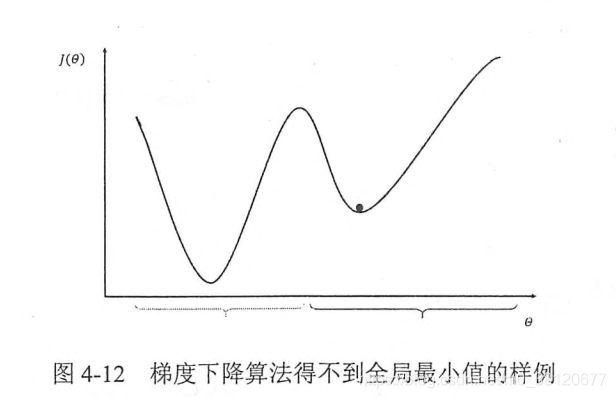
除此之外，梯度下降演算法的另外一個問題是計算時間太長，因為要在全部訓練資料上最小化損失，為了加速訓練過程，可以使用隨機梯度下降的演算法（stochastic gradient descent）。

神經網路的進一步優化

1. 學習率的設定
在訓練神經網路的過程中， 需要設定學習率控制引數更新的速度。
學習率決定了引數每次更新的幅度，如果幅度過大，那麼可能導致引數在極優值兩次來回移動。當學習率過小時，雖然能保證收斂性，但是會打打降低優化速度。
Tensorflow提供了一種更加靈活的學習率設定方法——指數衰減法tf.train.exponential_decay。通過該方法，可以使用較大學習率來快速得到一個比較優的解。然後隨著迭代的繼續逐步減小學習率，使模型在訓練的後期更加穩定。
2. 過擬合問題
在應用中，希望通過訓練出來的模型對未知資料給出判斷。模型在訓練資料上的表現並不一定代表他在位未知資料上的表現。
所謂過擬合，指的是當一個模型過為複雜之後，他可以很好的“記憶”每一個訓練資料中隨機噪音的部分而忘記要去“學習”訓練資料中通用的趨勢。
為了避免過擬合，一個非常常用的方法是正則化（regularization）。正則化的思想是在損失函式中加入刻畫模型複雜程度的指標。
3. 滑動平均模型

滑動平均模型——可以使模型在測試資料上更健壯（robust）。在採用隨機梯度下降演算法訓練神經網路時，滑動平均模型可以在一定程度上提高最終模型在測試資料上的表現。
Tensorflow中提供了tf.train.ExponentialMovingAverage來實現滑動平均模型。在初始化ExponentialMovingAverage時，需要提供一個衰減率（decay）。這個衰減率將用於控制模型更新的速度。ExponentialMovingAverage對每一個變數會維護一個影子變數（shadow variable），這個影子變數的初始值就是相應變數的初始值，而每次執行變數更新時，影子變數的值會更新為：

shadow_varibale=decay*shadow_varibale+(-1decay)*variable

其中，shadow_varibale為影子變數，variable為待更新的變數，decay為衰減率。decay決定了模型更新的速度，decay越大模型越趨於穩定，decay一般會設成非常接近1的數。