資料結構 | 線性排序
阿新 • • 發佈:2018-12-05
資料結構與演算法之美學習總結,這一課講了三個線性排序,這三種排序時間複雜度都是 。
目錄
1. 桶排序(Bucket sort)
把 個數據分到 個桶內,每個桶會有 個元素,每個桶內使用快速排序。桶排序的時間複雜度為 ,如果桶的數量越接近 ,就會退變成 。
桶排序對資料的要求很高:
- 桶與桶之間有天然大小順序;
- 資料在桶之間的分佈均勻。
桶排序適合用於外部排序: 資料存在外部磁碟中,資料量大而記憶體小,無法將資料全部載入到記憶體。
如果對 10 GB 的訂單按照金額排序,但是記憶體又不夠大,就可以對其進行桶排序。一般情況下 1 ~ 1000 的金額會比較多,那就對這部分再進行桶排序,直到記憶體可以裝得下。
2. 計數排序(Counting sort)
計數排序可以看做桶排序的特殊情況。 但是桶的大小粒度不一樣,一般來說,計數排序的桶會偏大但偏少。所以當資料的範圍 k 比要排序的資料 n 大得多,就不適合用計數排序。
計數排序只能給非負整數排序。 特殊情況的處理:
- 如果資料範圍是 [-1000, 1000],那麼我們給每一個數據加 1000,範圍就變為 [0, 2000];
- 如果資料精度是小數點後一位如,[0.1, 9.8],我們可以給每個資料乘以 10,就變為 [1, 98]。
計數的體現:
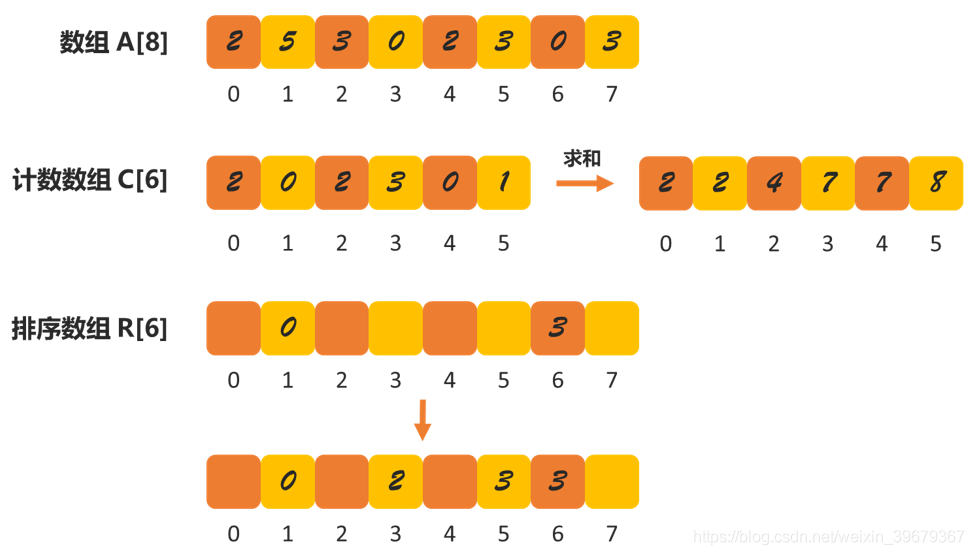
如上圖:以陣列 A = [2 5 3 0 2 3 0 3] 為例,說說計數排序的過程:
- 因為資料的範圍在 [0, 5],所以把資料分為 6 個桶,並存放在 C 陣列中(C 的下標代表資料,對應位置存放的是下標對應資料的數量);
- 然後對 C 中每個元素都求其前面元素與當前元素的和,即 C[i] = C[i - 1] + C[i];
- 請求一個存放排序好的資料的陣列,與 A 同樣大小;
- 從右往左對 A 排序,重複一下步驟:
- R[C[A[n]] - 1] = A[n]
- n = n - 1
計數排序的 Python 實現:
# copyright (c) strongnine
def countingSort(a):
n = len(a)
if n <= 1:
return
max = a[0]
for i in range(1, n):
if max < a[i]:
max = a[i]
c = [0 for i in range(max + 1)]
for i in range(n):
c[a[i]] += 1
for i in range(1, max + 1):
c[i] = c[i - 1] + c[i]
r = [0 for i in range(n)]
for i in range(n - 1, -1, -1):
index = c[a[i]] - 1
r[index] = a[i]
c[a[i]] -= 1
return r
if __name__ == '__main__':
a = [2, 5, 3, 0, 2, 3, 0, 3]
r = countingSort(a)
print(r)
3. 基數排序(Radix sort)
類似於對手機號的排序,資料的範圍很大,所以要分桶就不太行,所以不適合上面兩種方式。
過程: 先按照最後一位使用穩定的線性排序來排序手機號碼,再按照倒數第二位排序,直到弄完全部 11 位。注意使用的排序演算法一定要是穩定的。
對於不一樣長的資料,例如對單詞的排序,可以在每個單詞後面都補零,再排序。
基數排序的要求:
- 資料的「位」需要可以獨立分割出來比較;
- 位之間有遞進關係,即高位比低位高,就可以忽略更低位的大小。
4. 線性排序的侷限
線性排序演算法對於資料的要求都比較嚴苛,應用並不是很廣泛,但是如果資料的特徵很適合使用線性排序,那麼用起來就會很高效。
