matlab---矩陣運算函式
阿新 • • 發佈:2018-12-05
matlab—矩陣運算函式
- 矩陣的秩
任意一個矩陣都能通過初等行變換變成行階梯形,這個行階梯型所含非零行的行數就是矩陣的秩,矩陣的秩是矩陣的一個數字特徵,是矩陣初等變換的一個不變的量,對於矩陣研究具有重要意義。
matlab 求法:
給出矩陣a 直接輸入rank(a)即可。
示例:
>> a=[1,2,3;0,1,2;0,0,1];
>> rank(a)
結果是 ans=3;
- 矩陣的行列式:
一個n×n矩陣的行列式等於其任意行(或列)的元素與對應的代數餘子式乘積之和,即
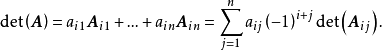
而用matlab 求就簡單多了 a是一個矩陣 只要輸入det(a)即可。
示例:
>> a=[1,2,3;0,1,2;0,0,1];
>> det(a)
- 矩陣的逆
設A是數域上的一個n階矩陣,若在相同數域上存在另一個n階矩陣B,使得: AB=BA=E ,則我們稱B是A的逆矩陣,而A則被稱為可逆矩陣。注:E為單位矩陣。
逆矩陣手算逆矩陣的方法都在這裡面。用matlab只需要輸入inv(a)即可。
示例:
>> a=[1,2,3;0,1,2;0,0,1];
>> inv(a)
- 矩陣的特徵值和特徵向量
設A是n階方陣,如果數λ和n維非零列向量x使關係式Ax=λx成立,那麼這樣的數λ稱為矩陣A特徵值,非零向量x稱為A的對應於特徵值λ的特徵向量。式Ax=λx也可寫成( A-λE)X=0。這是n個未知數n個方程的齊次線性方程組,它有非零解的充分必要條件是係數行列式| A-λE|=0。
矩陣的特徵值和特徵向量這裡面有詳細的解釋和計算方法
matlab實現[X,Y]=eig(a)x裡面存的是特徵向量,y的對角線上就是對應的特徵值,然後再用diag函式取出對角線上的值
示例:
a=[1,2,3;0,1,2;0,0,1];
[X,Y]=eig(a);
y=diag(Y);
X
y
- 矩陣的運算
拿來舉例子吧,如果你想讓兩個矩陣進行相乘,那矩陣的大小必須合法 nm 的矩陣 一定得乘 m*k的矩陣(n,k隨意)這是後直接乘就行c=a*b;但是你如果想讓矩陣中的相對應的元素進行乘法運算,此時就要用 . *c=a.*b
拿個示例來演示一下:
a=[1,2,3; 1,2,3; 1,2,3]; b=[1,1 1,1 1,1]; c=[1,1,1; 1,1,1; 1,1,1]; d=a*b f=a.*c
結果
d =
6 6
6 6
6 6
f =
1 2 3
1 2 3
1 2 3
此時 d 就是兩個矩陣相乘的結果,而f是矩陣中的每個元素對應相乘的結果。
