大綱：

• 樹、二叉樹
• 二叉查詢樹
• 平衡二叉查詢樹、紅黑樹
• 遞迴樹

一、樹（Tree）

1、樹的相關概念

（1）節點

其中，每個元素稱為“節點”；用來連線相鄰節點之間的關係，成為“父子關係”。其他概念：“父節點、子節點、兄弟節點，根節點，葉子節點或葉節點”
==》A 節點就是 B 節點的父節點，B 節點是 A 節點的子節點。B、C、D 這三個節點的父節點是同一個節點，所以它們之間互稱為兄弟節點。我們把沒有父節點的節點叫作根節點，也就是圖中的節點 E。我們把沒有子節點的節點叫作葉子節點或者葉節點，比如圖中的 G、H、I、J、K、L 都是葉子節點

（2）高度( Height )、深度( Depth )、層( Level )

不要混淆！

• 節點的高度 = 節點到葉子節點的最長路徑（邊數）
• 節點的深度 = 根節點到該節點所經歷的邊的個數
• 節點的層數 = 節點的深度 + 1
• 樹的高度 = 根節點的 高度

示例：

二、二叉樹(Binary Tree)

最常用 的樹結構

1、相關概念

（1）二叉樹

二叉樹：每個節點最多有兩個叉，也就是兩個子節點（左子結點、右子節點）。二叉樹並不要求每個節點都有兩個子節點，有的節點可以只有一個左子結點（或右子節點），有的節點沒有子節點。

（2）滿二叉樹

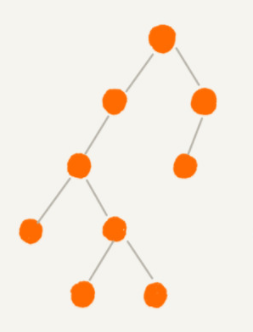
特點：葉子節點全都在最底層，除葉子節點外，每個結點都有左右兩個子節點。

（3）完全二叉樹

完全二叉樹：葉子節點都在最底下兩層，最後一層的葉子節點都靠左排列，並且除了最後一層，其他層的節點個數都要達到最大。

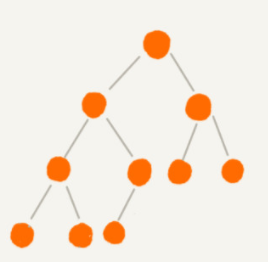
注意區分：

2、二叉樹的表示(儲存)

兩種儲存方法：
①基於指標或引用的二叉鏈式儲存法；
②基於陣列的順序儲存方法。

（1）鏈式儲存法——常用

每個節點有三個欄位，分別儲存：資料、指向左右子節點的指標。
==》只要通過根節點，就可以通過左右節點的指標，將整棵樹串起來。

（2）順序儲存法

一般情況下，為了方便計運算元節點，根節點會儲存在下標為 1 的位置。

• 將根節點儲存在下標 i = 1 的位置，其左節點儲存在下標 2 * i = 2 的位置，右子節點儲存在 2 * i + 1 = 3的位置。
• 依次類推：
  • 若結點 X 儲存在陣列中下標為 i 的位置，
  • 其左節點下標： 2 * i
  • 其右節點下標： 2 * i + 1
  • 其父節點下標：i / 2

（3）分析

若二叉樹為完全二叉樹，則陣列儲存是最節省記憶體的一種方式（不需要儲存額外的左右子節點的指標）
==》堆——本質：完全二叉樹，最常用的儲存方式就是陣列。

3、二叉樹遍歷

（1）方法

三種方法：前序遍歷、中序遍歷、後序遍歷
==》節點與它的左右子樹節點遍歷的先後順序：中代表該節點，左代表其左子樹，右代表其右子樹。

• 前序遍歷：中、左、右
• 中序遍歷：左、中、右
• 後序遍歷：左、右、中

（2）程式碼實現

關鍵點：遞迴程式碼 《== 遞迴公式

前序遍歷的遞推公式：
preOrder(r) = print r->preOrder(r->left)->preOrder(r->right)

中序遍歷的遞推公式：
inOrder(r) = inOrder(r->left)->print r->inOrder(r->right)

後序遍歷的遞推公式：
postOrder(r) = postOrder(r->left)->postOrder(r->right)->print r

遞迴程式碼：
==》遍歷時間複雜度：O(n)

// 虛擬碼

void preOrder(Node * root) {
	if(root == null)
		return;
	print root;          // 列印 root 節點
	preOrder(root->left);
	preOrder(root->right);
}

void inOrder(Node * root) {
	if(root == null)
		return;
	inOrder(root->left);
	print root;          // 列印 root 節點
	inOrder(root->right);
}

void postOrder(Node * root) {
	if(root == null)
		return;
	postOrder(root->left);
	postOrder(root->right);
	print root;          // 列印 root 節點
}

三、二叉查詢樹

特點：支援動態資料集合的快速插入、刪除、查詢操作。

1、二叉查詢樹（Binary Search Tree）

二叉查詢樹是二叉樹中最常用的一種型別，也稱二叉搜尋樹。可以快速插入、刪除、查詢操作。

結構要求：樹中的任何一個節點，其左子樹的每個節點的值，都要小於該節點的值，而右子樹節點的值都大於這個節點的值。

2、查詢操作

目標：查詢一個結點
過程：先取根節點，若它等於要查詢的資料，則返回；若要查詢的資料的值比根節點小，則在左子樹中遞迴查詢；若要查詢的資料的值比根節點大，則在右子樹中遞迴查詢。

public class BinarySearchTree {
	private Node tree;

	public Node find(int data){
		while(p != null){
			if (data < p.data)
				p = p.left;
			else if(data > p.data)
				p = p.right;
			else
				return p;
		}
		return null;
	}

	public static class Node {
		private int data;
		private Node left;
		private Node right;

		public Node(int data){
			this.data = data;
		}
	}
}

3、插入操作

類似查詢操作，新插入的資料一般都在葉子節點上
==》只需要從根節點開始，依次比較要插入的資料和節點的大小關係。

過程：若要插入的資料比節點的資料大，並且節點的右子樹為空，則將新資料直接插入到右子節點的位置；若不為空，則遞迴遍歷右子樹，查詢插入位置。同理，若要插入的資料比節點的資料小，並且節點的左子樹為空，則將新資料直接插入到左子節點的位置；若不為空，則遞迴遍歷左子樹，查詢插入位置。

public void insert(int data) {
	if(tree == null){
		tree = new Node(data);
		return 0;
	}

	Node p = tree;
	while(p != null){
		if(data > p.data) {
			if(p.right == null) {
				p.right = new Node(data);
				return;
			}
			p = p.right;
		}
		else { // data < p.data
			if(p.left == null){
				p.left = new Node(data);
				return;
			}
		p = p.left;
		}
	}
}

4、刪除操作

針對要刪除節點的子節點個數的不同，分以下三種情況處理。

• 若要刪除的節點沒有子節點，則只需之間將其父節點中，指向要刪除節點的指標置為null。
• 若要刪除的節點只有一個子節點（只有左子節點或右子節點），只需要更新父節點中，指向要刪除節點的指標，讓其指向要刪除節點的子節點即可。
• 若要刪除的節點有兩個子節點。首先，需要找到該節點的右子樹中最小節點，將它替換到要刪除的節點上，然後再刪除這個最小節點（∵最小節點無左子節點）。

public void delete(int data){
	Node p = tree; // p 指向要刪除的節點，初始化指向根節點
	Node pp = null; // pp 記錄 p 的父節點
	// 找到要刪除的節點
	while (p != null && p.data != data){
		pp = p;
		if(data > p.data)
			p = p.right;
		else
			p = p.left;
	}	
	if (p == null)
		return;     // 沒有找到

	// 要刪除的節點有兩個子節點
	if(p.left != null && p.right != null){
		// 查詢右子樹中最小節點
		Node minP = p.right;
		Node minPP = p;  // minPP 表示 minP 的父節點
		while (minP.left != null){
			minPP = minP;
			minP = minP.left;
		}
		// 將 minP 的資料替換到 p 中
		p.data = minP.data;  
		// 下面變成刪除 minP
		p = minP;
		pp = minPP;
	}

	// 刪除節點是葉子節點或者僅有一個節點
	Node child;  // p 的子節點
	if(p.left != null)
		child = p.left;
	else if(p.right != null)
		child = p.right;
	else
		child = null;

	// 刪除的是根節點
	if(pp == null)
		tree = child;
	else if(pp.left == p)
		pp.left = child;
	else pp.right = child;
}

實際：非常簡單、取巧的方法——單純地將要刪除的節點標記為“已刪除”，但並不真正從樹中將這個節點去掉。
==》雖較浪費記憶體空間，但刪除操作就變得簡單多了，且並沒有增加插入、查詢操作程式碼實現的難度。

5、其他操作

還支援快速查詢最大節點、最小節點、前驅節點和後繼節點。

中序遍歷二叉查詢樹
==》輸出：有序的資料序列，時間複雜度為 O(n)
==》也稱：二叉排序樹

四、支援重複資料的二叉查詢樹

實際中常在二叉查詢樹中儲存的是包含很多欄位的物件。並利用某個欄位作為鍵值(key)來構建二叉查詢樹。物件中的其他欄位稱為衛星資料。

1、插入操作

在二叉查詢樹中儲存兩個物件鍵值相同的方法：

• 二叉查詢樹中每個節點不僅儲存一個數據
  ==》通過連結串列和支援動態擴容的陣列等資料結構，把值相同的資料都儲存在同一個節點上。
• 每個節點仍儲存一個數據。在查詢插入位置的過程中，若遇到一個節點的值與要插入資料的值相同，則將這個要插入的資料放在這個節點的右子樹，即，將新插入的資料當作大於這個節點的值來處理。

2、查詢操作

當要查詢資料時，若遇到值相同的節點，不停止查詢操作，而繼續在右子樹中查詢，知直到遇到葉子節點，才停止。
==》可將鍵值等於要查詢值得所有節點都找出來。

3、刪除操作

過程：首先找到每個要刪除的節點，然後按照前面的刪除操作方法依次刪除節點。

五、時間複雜度分析

不同的二叉查詢樹形態各式各樣
==》影響查詢、插入、刪除操作的執行效率

情況一：最糟糕——退化為連結串列（根節點的左右子樹極度不平衡）
==》查詢的時間複雜度：O(n)

情況二：最理想——完全二叉樹（或滿二叉樹）
==》插入、刪除和查詢的時間複雜度：O(height)
==》求一棵包含n個節點的完全二叉樹的高度？
完全二叉樹的高度小於等於 log2n。

==》需要構建一種不管怎麼刪除、插入資料，在任何時候，都能保持任意節點左右子樹都比較平衡的二叉查詢樹——平衡二叉查詢樹

平衡二叉查詢樹的高度接近 logn，所以插入、刪除、查詢操作的時間複雜度也比較穩定，是 O(logn)。

六、思考

問題：既然有了這麼高效的散列表，使用二叉樹的地方是不是都可以替換成散列表呢？有沒有哪些地方是散列表做不了，必須要用二叉樹來做的呢？

• 散列表中的資料是無序儲存的，如果要輸出有序的資料，需要先進行排序。而對於二叉查詢樹來說，我們只需要中序遍歷，就可以在 O(n) 的時間複雜度內，輸出有序的資料序列。
• 散列表擴容耗時很多，而且當遇到雜湊衝突時，效能不穩定，儘管二叉查詢樹的效能不穩定，但是在工程中，我們最常用的平衡二叉查詢樹的效能非常穩定，時間複雜度穩定在 O(logn)。
• 籠統地來說，儘管散列表的查詢等操作的時間複雜度是常量級的，但因為雜湊衝突的存在，這個常量不一定比 logn 小，所以實際的查詢速度可能不一定比 O(logn) 快。加上雜湊函式的耗時，也不一定就比平衡二叉查詢樹的效率高。
• 散列表的構造比二叉查詢樹要複雜，需要考慮的東西很多。比如雜湊函式的設計、衝突解決辦法、擴容、縮容等。平衡二叉查詢樹只需要考慮平衡性這一個問題，而且這個問題的解決方案比較成熟、固定。
• 為了避免過多的雜湊衝突，散列表裝載因子不能太大，特別是是基於開放定址法解決衝突的散列表，不然會浪費一定的儲存空間。